倒角二十面體
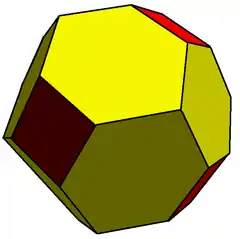
在幾何學中,倒角十二面體是一種凸多面體,可由十二面體經過倒角變換構成,也可由菱形三十面體截去20個相鄰三個面的頂點構成。倒角十二面體六邊形面可以是等邊六邊形但不是正六邊形。
 | ||
| 類別 | 凸多面體 | |
|---|---|---|
| 對偶多面體 | triakis icosidodecahedron | |
| 數學表示法 | ||
| 康威表示法 | cI t3daI | |
| 性質 | ||
| 面 | 50 | |
| 邊 | 120 | |
| 頂點 | 72 | |
| 歐拉特徵數 | F=50, E=120, V=72 (χ=2) | |
| 組成與佈局 | ||
| 面的種類 | 20個正三角形 30個六邊形 | |
| 頂點佈局 | (24) 3.6.6 (12) 6.6.6 | |
| 對稱性 | ||
| 對稱群 | Ih, [5,3], (*532) | |
| 旋轉對稱群 | Ih群 | |
| 特性 | ||
| 凸 | ||
| 圖像 | ||
| ||
參見
參考文獻
- Goldberg, Michael. . Tohoku Mathematical Journal. 1937 [2016-01-08]. (原始内容存档于2019-10-21).
- Joseph D. Clinton, Clinton’s Equal Central Angle Conjecture (页面存档备份,存于)
- Hart, George. . Senechal, Marjorie (编). 2nd. Springer. 2012: 125–138. doi:10.1007/978-0-387-92714-5_9.
- Hart, George. . Simons Science News. June 18, 2013 [2016-01-08]. (原始内容存档于2017-02-27).
- Antoine Deza, Michel Deza, Viatcheslav Grishukhin, Fullerenes and coordination polyhedra versus half-cube embeddings, 1998 PDF (页面存档备份,存于) (p. 72 Fig. 26. Chamfered tetrahedron)
- Deza, A.; Deza, M.; Grishukhin, V., , Discrete Mathematics, 1998, 192 (1): 41–80 [2016-01-08], doi:10.1016/S0012-365X(98)00065-X, (原始内容存档于2007-02-06).
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.