倒角十二面體
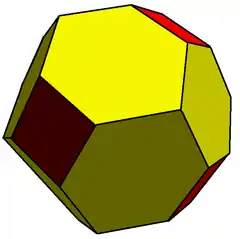
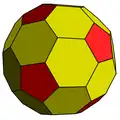
在幾何學中,倒角十二面體是一種凸多面體,由12個五邊形和30個六邊形組成,那30個六邊形是全等的,惟非正六邊形。倒角十二面體共有42個面、120個邊和80個頂點,是五角化截半二十面體的對偶多面體。
 | ||||
| 類別 | 凸多面體 | |||
|---|---|---|---|---|
| 對偶多面體 | 五角化截半二十面體 | |||
| 數學表示法 | ||||
| 康威表示法 | cD t5daD | |||
| 性質 | ||||
| 面 | 42 | |||
| 邊 | 120 | |||
| 頂點 | 80 | |||
| 歐拉特徵數 | F=42, E=120, V=80 (χ=2) | |||
| 組成與佈局 | ||||
| 頂點佈局 | (60) 5.6.6 (20) 6.6.6 | |||
| 對稱性 | ||||
| 對稱群 | Ih, [4,3], (*432) | |||
| 旋轉對稱群 | Ih群 | |||
| 特性 | ||||
| 凸 | ||||
| 圖像 | ||||
| ||||
是由正十二面體經由倒角變換產生的多面體,即是將正十二面體中的30條邊以六邊形取代所形成的凸多面體,因此倒角二十面體共有30個六邊形,而原本的五邊形被保留,但倒角變換產生的六邊形非正邊形。
等價的多面體
交錯截角菱形三十面體與倒角十二面體是相同的多面體,但是構成方式不太相同。交錯截角菱形三十面體是經過交錯截角變換構成的,即將其頂點不全部截掉,而是交錯截去,康威符號計為h,對於菱形三十面體會造成兩種結果:僅切去有五個相鄰面的頂點以及僅切去有三個相鄰面的頂點,而僅有切去相鄰五個面的頂點的多面體與倒角二十面體等價,因此若稱為交錯截角菱形三十面體存在歧意:可能為倒角二十面體或倒角十二面體。
交錯截角菱形三十面體就是切去頂點的菱形三十面體,但是只能切去五個相鄰面的頂點。這12個五階頂點(有五個相鄰面的頂點)可以被截成等長的,這使得原來的菱形面變成非正六邊形,截去的頂點成為正五邊形。它在頂點配置為6.6.6的兩面角是arccos(-1/sqrt(5)) = 116.565度,另一個在5.6.6的兩面角近似值為121.717 度。
參考文獻
- Deza, A.; Deza, M.; Grishukhin, V., , Discrete Mathematics, 1998, 192 (1): 41–80 [2013-03-19], doi:10.1016/S0012-365X(98)00065-X, (原始内容存档于2007-02-06).
- VTML polyhedral generator(页面存档备份,存于) Try "t5daD" (康威多面體表示法)
- Zometool model
- Fullerene C80
- (Number 7 -Ih)
- (页面存档备份,存于)
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.