八角柱

在幾何學中，八角柱是一種多面體，是柱體的一種，是指底面是八邊形的柱體，也是第六種有無限多成員的柱體集合（八角柱包含所有底面是八邊形的柱體，即是是凹八邊形）。所有八角柱都有10個面，24個邊和16個頂點[1]。所有八角柱都是十面體。

正八角柱
八角柱
類別柱體
柱狀均勻多面體
對偶多面體雙八角錐在维基数据编辑
識別
名稱正八角柱
參考索引U76(f)
鮑爾斯縮寫
op在维基数据编辑
數學表示法
考克斯特符號
node_1 2 node_1 8 node 
node_1 2 node_1 4 node_1 
施萊夫利符號t{2,8}
tr{4,2}
s2{2,8}
{8}×{}
t{4}×{}在维基数据编辑
威佐夫符號
2 8 | 2
康威表示法P8在维基数据编辑
性質
面10
邊24
頂點16
歐拉特徵數F=10, E=24, V=16 （χ=2）
組成與佈局
面的種類2個八邊形
8個正方形
面的佈局
8{4}+2{8}
頂點圖4.4.8
對稱性
對稱群D8h, [8,2], (*822), order 32
旋轉對稱群
D8, [8,2]+, (822), order 16
特性
凸、 zonohedron
圖像

4.4.8
（頂點圖）

雙八角錐
（對偶多面體）
（展開圖）

如果八角柱每個面都是正多邊形，則它是半正多面體。

小斜方截半立方体切去相对的两个正四角帐塔就可以得到一个八角柱。

性質

體積

若一正八角柱的邊長皆為1，則八角柱的體積為：[2]

表面積

若一正八角柱的邊長皆為1，則八角柱的表面積為：[2]

對稱性
圖像
對稱群 D4h, [2,4], (*422) D4d, [2+,8], (2*4)
Constructiopn tr{4,2} or t{4}×{}, node_1 2 node_1 4 node_1  s2{2,8}, node_h 2 node_h 8 node_1 

三維鑲嵌和多胞體

有正八角柱的三維鑲嵌:

截角四角柱堆砌
node_1 4 node_1 4 node 2 node_1 infin node 		 大斜方截半正方體堆砌
node_1 4 node_1 3 node_1 4 node_1 		 小斜方截半正方體堆砌
node_1 4 node_1 3 node 4 node_1 

有胞是正八角柱的多胞體:

大斜方截半超立方體
node_1 4 node_1 3 node 3 node_1 		 小斜方截半超立方體
node_1 4 node_1 3 node_1 3 node_1 

在其他領域
  • 在光學上，八角柱的棱鏡被用於在電影放映機產生不閃爍的圖像。
  • 十三行博物館的主要建築物是一個斜八角柱，象徵時間久遠遺跡毀壞無法還原的歷史真相[3][4]。
圖中棕色建築物即斜八角柱的十三行博物館

相關多面體與鑲嵌
正多邊形柱體系列
對稱群 3 4 5 6 7 8 9 10 11 12
[2n,2]
[n,2]
[2n,2+]		 node_1 3 node 2 node_1  node_1 4 node 2 node_1 
node_1 2 node_1 2 node_1 
node_1 4 node_h 2 node_h 		 node_1 5 node 2 node_1  node_1 6 node 2 node_1 
node_1 3 node_1 2 node_1 
node_1 6 node_h 2 node_h 		 node_1 7 node 2 node_1  node_1 8 node 2 node_1 
node_1 4 node_1 2 node_1 
node_1 8 node_h 2 node_h 		 node_1 9 node 2 node_1  node_1 10 node 2 node_1 
node_1 5 node_1 2 node_1 
node_1 10 node_h 2 node_h 		 node_1 11 node 2 node_1  node_1 12 node 2 node_1 
node_1 6 node_1 2 node_1 
node_1 12 node_h 2 node_h 
圖像





球面多面體
圖像



柱體形式半正鑲嵌系列：
球面鑲嵌 柱體 歐式鑲嵌
仿緊空間		 雙曲鑲嵌
非緊空間

t{2,1}
node 2 node_1 
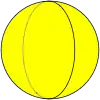t{2,2}
node_1 2 node 2 node_1 
t{3,2}
node_1 3 node 2 node_1 
{4,2}
node_1 4 node 2 node_1 
t{5,2}
node_1 5 node 2 node_1 
t{6,2}
node_1 6 node 2 node_1 
t{7,2}
node_1 7 node 2 node_1 
t{8,2}
node_1 8 node 2 node_1 		 ...
t{2,∞}
node_1 infin node 2 node_1 
t{2,iπ/λ}
node_1 ultra node 2 node_1 
大斜方截半四階多面體和鑲嵌系列： 4.8.2n
對稱群
*n42
[n,4]		 球面鑲嵌 歐氏鑲嵌 緊湊型雙曲鑲嵌 仿緊空間 非緊空間
*242
[2,4]
D4h		 *342
[3,4]
Oh		 *442
[4,4]
P4m		 *542
[5,4]		 *642
[6,4]		 *742
[7,4]		 *842
[8,4]...		 *∞42
[∞,4]		  
[iπ/λ,4]
大斜方截半
頂點
4.8.4
4.8.6
4.8.8
4.8.10
4.8.12
4.8.14
4.8.16
4.8.∞
4.8.∞
考克斯特紀號
施萊夫利符號		 node_1 2 node_1 4 node_1 
tr{2,4}		 node_1 3 node_1 4 node_1 
tr{3,4}		 node_1 4 node_1 4 node_1 
tr{4,4}		 node_1 5 node_1 4 node_1 
tr{5,4}		 node_1 6 node_1 4 node_1 
tr{6,4}		 node_1 7 node_1 4 node_1 
tr{7,4}		 node_1 8 node_1 4 node_1 
tr{8,4}		 node_1 infin node_1 4 node_1 
tr{∞,4}		 node_1 ultra node_1 4 node_1 
tr{iπ/λ,4}
大斜方截半
對偶
V4.8.4
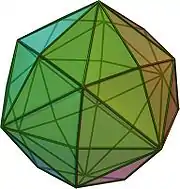V4.8.6
V4.8.8
V4.8.10
V4.8.12
V4.8.14
V4.8.16
V4.8.∞
V4.8.∞
考克斯特紀號 node_f1 2 node_f1 4 node_f1  node_f1 3 node_f1 4 node_f1  node_f1 4 node_f1 4 node_f1  node_f1 5 node_f1 4 node_f1  node_f1 6 node_f1 4 node_f1  node_f1 7 node_f1 4 node_f1  node_f1 8 node_f1 4 node_f1  node_f1 infin node_f1 4 node_f1  node_f1 ultra node_f1 4 node_f1 

參考文獻
  1. David I. McCooey. . [2022-09-14]. （原始内容存档于2022-09-14）.
  2. Weisstein, Eric W. (编). . at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. （原始内容存档于2021-10-20） （英语）.
  3. . sshm.ntpc.gov.tw. （原始内容存档于2013-07-18）. 八角柱建築 在最後一段
  4. . sshm.ntpc.gov.tw. 2017-11-22 [2022-06-06]. （原始内容存档于2021-01-24）.

外部連結
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.