八階三角形鑲嵌

如要得到一半的對稱性[1⁺,8,3] = [(4,3,3)]可透過將三角形以兩種顏色交錯塗色而得到。

正八邊形鑲嵌加上 *444 鏡射線， .

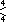
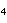在[(4,4,4)] 對稱性中， 有十五個(七個特殊)透過移除鏡射線和交錯變換的子群。 若一個鑲嵌中的階數為偶數，則可移除鏡射線，並將相鄰、分開的階去除一半。移除兩條鏡射線會變成半階偏轉點，其為移除鏡射線交會的地方。 在這些圖像中，基本域交替著色為黑色和白色， 而鏡射線位於兩種顏色交會的邊上。 在每個基本域上添加三個平分鏡射線會產生832對稱性。 子群指數-8群， [(1⁺,4,1⁺,4,1⁺,4)] (222222)是[(4,4,4)]的換位子群。

一個更大的子群構造為[(4,4,4^*)]，指數為8，可作為將部分頂點去除的(2*2222)，也就是(*22222222)。 此對稱性可透過加入平分基本域的鏡射線增倍為842對稱性。 此對稱線可由6擴展，透過在每個域加入三個平分鏡射線，作為832對稱性。

[(4,4,4)] (*444)的子群

子群指數	1	2			4
圖形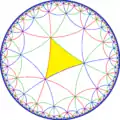
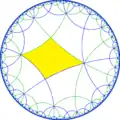考斯特圖	[(4,4,4)]	[(1+,4,4,4)] =	[(4,1+,4,4)] =	[(4,4,1+,4)] =	[(1+,4,1+,4,4)]	[(4+,4+,4)]
軌形	*444	*4242			2*222	222×
圖像
考斯特		[(4,4+,4)]	[(4,4,4+)]	[(4+,4,4)]	[(4,1+,4,1+,4)]	[(1+,4,4,1+,4)] =
軌形		4*22			2*222
導向子群
指數	2	4			8
圖像
考斯特	[(4,4,4)]+	[(4,4+,4)]+ =	[(4,4,4+)]+ =	[(4+,4,4)]+ =	[(4,1+,4,1+,4)]+ =
軌形	4242			222222
根源子群
指數	8			16
圖像
考斯特	[(4,4*,4)]	[(4,4,4*)]	[(4*,4,4)]	[(4,4*,4)]+	[(4,4,4*)]+	[(4*,4,4)]+
軌形	*22222222			22222222

{3,3,8}的蜂巢體的頂點圖為{3,8}。

多面体				欧式镶嵌	双曲镶嵌
{3,2}	{3,3}	{3,4}	{3,5}	{3,6}	{3,7}	{3,8}	{3,9}	...	{3,∞)

球面	雙曲鑲嵌
{2,8}	{3,8}	{4,8}	{5,8}	{6,8}	{7,8}	{8,8}	...	{∞,8}

在Wythoff構建中，有十個雙曲正鑲嵌可以由正八邊形鑲嵌以及八階正三角形鑲嵌構造而來。

此外，八階三角形鑲嵌作為一種無窮抽象多胞形，可以具象化為一種扭歪無限面體，該扭歪多面體皆由三角形組成，每個頂點都是8個三角形的公共頂點，其結構可以看做是依照立方晶格排列的扭稜立方體移除其正方形面所構成的幾何結構。[1]

维基共享资源上的相关多媒体资源：八階三角形鑲嵌

• 八階四面體堆砌

• 埃里克·韦斯坦因. . MathWorld.
• 埃里克·韦斯坦因. . MathWorld.
• 雙曲鑲嵌以及球面鑲嵌（页面存档备份，存于）
• KaleidoTile 3: Educational software to create spherical, planar and hyperbolic tilings （页面存档备份，存于）
• 雙曲鑲嵌, Don Hatch（页面存档备份，存于）