六方偏方面體
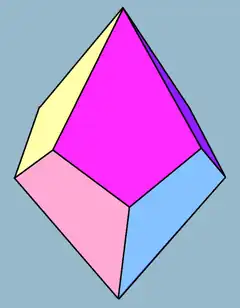
在幾何學中,六方偏方面體是一個由12個全等的鳶形組成的多面體,是十二面體的一種,同時也是鳶形多面體。其對偶多面體為六角反稜柱。在化學中,原子的晶體結構可以在空間中以六方偏方面體形狀的胞重複排列。[1]
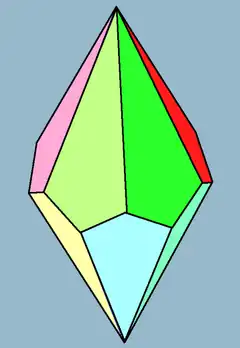 | ||
| 類別 | 偏方面體 | |
|---|---|---|
| 對偶多面體 | 六角反稜柱 | |
| 數學表示法 | ||
| 考克斯特符號 | ||
| 性質 | ||
| 面 | 12 | |
| 邊 | 24 | |
| 頂點 | 14 | |
| 歐拉特徵數 | F=12, E=24, V=14 (χ=2) | |
| 組成與佈局 | ||
| 面的種類 | 12個箏形 | |
| 面的佈局 | V6.3.3.3 | |
| 對稱性 | ||
| 對稱群 | D6d, [2+,12], (2*6), 24階 | |
| 旋轉對稱群 | D6, [2,6]+, (226), order 12 | |
| 特性 | ||
| 凸、面可遞 | ||
| 圖像 | ||
| ||
變體
| 種類 | 扭曲的梯形、等面 | 不等面 | 不等面且扭曲 | |
|---|---|---|---|---|
| 對稱性 | D6, (662), [6,2]+, 12階 | C6v, (*66), [6], 12階 | C6, (66), [6]+, 6階 | |
| 圖像 (n=6) |
 |
 |
 |
 |
| 展開圖 |  |
 |
 |
 |
相關多面體
| 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | ... |
|---|---|---|---|---|---|---|---|---|---|---|---|
 |
 |
 |
 |
 |
 |
 |
 |
 |
|||
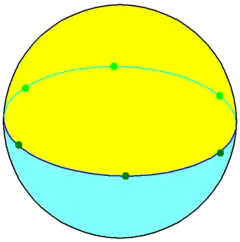
| 球面投影 | |||||||||||
 |
 |
 |
 |
 |
 |
 |
 |
 |
|||
| 對稱群:[6,2], (*622) | [6,2]+, (622) | [1+,6,2], (322) | [6,2+], (2*3) | ||||||
|---|---|---|---|---|---|---|---|---|---|
 |
 |
 |
 |
 |
 |
 |
 | ||
| {6,2} | t{6,2} | r{6,2} | 2t{6,2}=t{2,6} | 2r{6,2}={2,6} | rr{6,2} | tr{6,2} | sr{6,2} | h{6,2} | s{2,6} |
| 半正對偶 | |||||||||
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
| V62 | V122 | V62 | V4.4.6 | V26 | V4.4.6 | V4.4.12 | V3.3.3.6 | V32 | V3.3.3.3 |
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.
