十六面體

正十四角柱

十四角柱是一種底面為十四邊形的柱體，是十六面體的一種，其由16個面、28個頂點和42個邊組成。正十四角柱代表每個面都是正多邊形的十四角柱，其每個頂點都是2個正方形和1個十四邊形的公共頂點，頂點圖以${\displaystyle 4{.}4{.}14}$表示，在施萊夫利符號中可以利用{14}×{} 或 t{2, 14}來表示；在考克斯特—迪肯符号中可以利用來表示；在威佐夫符號中可以利用2 14 | 2來表示；在康威多面體表示法中可以利用P14來表示。底邊長為${\displaystyle s}$、高為${\displaystyle h}$的正十四角柱體積${\displaystyle V}$和表面積${\displaystyle S}$為[4]：

${\displaystyle V={\frac {7hs^{2}\cot {\frac {\pi }{14}}}{2}}\approx 15.3345hs^{2}}$

${\displaystyle S=7s\left(2h+s\cot {\frac {\pi }{14}}\right)\approx 7s\left(2h+4.38129s\right)}$

十五角錐

十五角錐是一種底面為十五邊形的錐體，是十六面體的一種，其具有16個面、30條邊和16個頂點，其對偶多面體是自己本身[5]。正十五角錐是一種底面為正十五邊形的十五角錐。底邊長為${\displaystyle s}$、高為${\displaystyle h}$的正十五角錐體積${\displaystyle V}$和表面積${\displaystyle S}$為[5]：

${\displaystyle V={\frac {5hs^{2}\cot {\frac {\pi }{15}}}{4}}\approx 5.88079hs^{2}}$

${\displaystyle S={\frac {15s\left({\sqrt {4h^{2}+s^{2}\cot ^{2}{\frac {\pi }{15}}}}+s\cot {\frac {\pi }{15}}\right)}{4}}\approx 3.75s\left({\sqrt {4h^{2}+22.1335s^{2}}}+4.70463s\right)}$

正七角反角柱

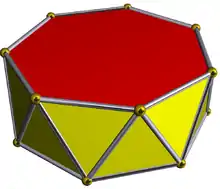
七角反角柱是一種底面為七邊形的反角柱，是十六面體的一種，其具有16個面、28條邊和14個頂點[6]，對偶多面體為七方偏方面體[7]。正七角反角柱是指所有面皆為正多邊形的七角反角柱。若一個正七角反角柱邊長為單位長，則其體積為：[7]

${\displaystyle V={\frac {\sqrt {7\left(48\left(\cos ^{2}{\frac {\pi }{7}}\right)+22\cos {\frac {\pi }{7}}-5\right)}}{6}}\approx 3.23391529}$

雙四角錐反角柱

雙四角錐反角柱是一種以四邊形為基底的角錐反角柱，是十六面體的一種，可以視為由兩個四角錐以底面對底面地疊合到四角反稜柱的兩個底面上所構成的立體，由16個三角形面、24條邊和10個頂點所組成[8]。若雙四角錐反角柱的基底為正方形，則這個立體稱為正雙四角錐反角柱。正雙四角錐反角柱是一種詹森多面體，這意味著其所有的構成面都是正多邊形，同時由於構成面皆為三角形，因此也是一種正三角面多面體。[9]

若雙四角錐反角柱的邊長為單位長，則其體積${\displaystyle V}$和表面積${\displaystyle S}$為：[10]

${\displaystyle V={\frac {{\sqrt[{4}]{2}}\left(1+{\sqrt {2}}+{\sqrt[{4}]{2}}\right)}{3}}}$[10]

${\displaystyle ={\frac {{\sqrt {2}}+{\sqrt {4+3{\sqrt {2}}}}}{3}}}$[8]

${\displaystyle \approx 1.42840450}$

${\displaystyle S=\,}$${\displaystyle {{4}\,{\sqrt {3}}}\approx 6.9282032302755}$

雙八角錐

雙八角錐是一種以八邊形為基底的雙錐體，是十六面體的一種，其可以視為兩個八角錐的底面對底面疊合成的立體，由16個面、24條邊和10個頂點組成[11][12]，對偶多面體為八角柱[12][13]。

雙八角錐在施萊夫利符號中可以用{ }+{8}來表示，在考克斯特符號中可以用來表示，在康威多面體表示法中可以用dP8來表示。

八方偏方面體是一種以八邊形為基底的偏方面體，是十六面體的一種，同時也是鳶形多面體，是偏方面體系列的第六個成員，由十六個全等的鷂形、32條邊和18個頂點組成，對偶多面體是八角反角柱。[14][15]八方偏方面體的頂點有兩種，分別為8個鳶形的公共頂點和3個鳶形的公共頂點。

八方偏方面體是一個等面圖形，即面可遞多面體，其所有面都相等。更具體來說，其不僅所有面都全等，且面與面必須能在其對稱性上傳遞，也就是說，面必須位於同一個對稱性軌道內。這種凸多面體是能做成公正的骰子的形狀。[16]

八方偏方面體在施萊夫利符號中可以用{ }⨁{8}來表示，在考克斯特符號中可以用或來表示，在康威多面體表示法中可以用dA8來表示。

在詹森多面體中有3種立體具有十六個面[17]，分別為五角錐反角柱、雙四角錐反角柱和側錐十二面體。

五角錐反角柱

雙四角錐反角柱

側錐十二面體