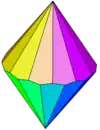
七方偏方面體
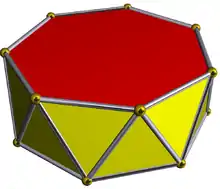
在幾何學中,七方偏方面體是一個由14個全等的鳶形組成的多面體,是十四面體的一種[1],同時也是鳶形多面體,是偏方面體系列的第五個成員。
 | ||
| 類別 | 偏方面體 | |
|---|---|---|
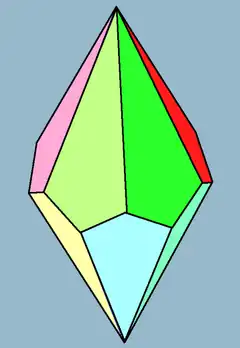
| 對偶多面體 | 七角反棱柱 | |
| 數學表示法 | ||
| 考克斯特符號 | ||
| 康威表示法 | dA7 | |
| 性質 | ||
| 面 | 14 | |
| 邊 | 28 | |
| 頂點 | 16 | |
| 歐拉特徵數 | F=14, E=28, V=16 (χ=2) | |
| 組成與佈局 | ||
| 面的種類 | 14個箏形 | |
| 面的佈局 | V7.3.3.3 | |
| 對稱性 | ||
| 對稱群 | D7d, [2+,14], (2*7), 28階 | |
| 旋轉對稱群 | D7, [2,7]+, (227), 14階 | |
| 特性 | ||
| 凸、面可遞 | ||
| 圖像 | ||
| ||
七方偏方面體是一個等面圖形,即面可遞多面體,其所有面都相等。更具體來說,其不僅所有面都全等,且面與面必須能在其對稱性上傳遞,也就是說,面必須位於同一個對稱性軌道內。這種凸多面體是能做成公正的骰子的形狀。[2]因此其可以做成一種十四面骰子[3]。
性質
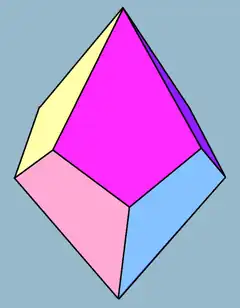
七方偏方面體共由14個面、28條邊和16個頂點組成。組成七方偏方面體的14個面都是鳶形,而組成七方偏方面體的16個頂點有2個是7個鳶形的公共頂點,另外14個是3個鳶形的公共頂點。[4]
對稱性
七方偏方面體的對稱性是28階的D7d二面體群。 其旋轉群為14階的D7群。
變體
從D7d群(28階)到D7(14階)的對稱性有一個自由度能將全等的鳶形轉變為具有3種邊長的全等四邊形,稱為扭曲鳶形,其所形成的偏方面體稱為扭曲偏方面體。
如果圍繞上下兩頂點的鳶形不是扭曲的,但是具有兩種形狀,則這個七方偏方面體只能具有循環的14階C7v對稱性,稱為不等或不對稱的七方偏方面體。其對偶多面體是一個等面與底面半徑不相等的七角反角柱。
如果組成七方偏方面體的鳶形是扭曲的,且有兩種形狀,則這個七方偏方面體只能具有循環的7階C7對稱性,稱為不等面扭曲七方偏方面體。
參考文獻
- Verhetsel, Kilian and Pellerin, Jeanne and Remacle, Jean-François. . ACM Transactions on Graphics (TOG) (ACM New York, NY, USA). 2019, 38 (4): 1–13.
- McLean, K. Robin, , The Mathematical Gazette, 1990, 74 (469): 243–256, JSTOR 3619822, doi:10.2307/3619822.
- . aleakybos.ch. [2022-12-30]. (原始内容存档于2022-12-30).
- . dmccooey.com. [2022-12-30]. (原始内容存档于2019-09-29).
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.