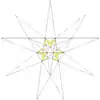
十複合正四面體
在幾何學中,十複合正四面體(英語:,又稱為Tetrahedron 10-Compound),是一種多面體複合體,由10個正四面體組合而成。這個複合幾何結構最早由埃德蒙·赫斯於1876年描述。[1]十複合正四面體可以視為是一種複合體也可以視為一種星形二十面體[2]:45,其可由2個互為鏡像的五複合正四面體複合而成[3],也可以進一步地與大三角六邊形二十面體複合成第二星形二十面體。[2]:47
 | ||||||||||||
| 類別 | 複合正多面體 星形二十面體 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 對偶多面體 | 十複合正四面體(自身對偶) | |||||||||||
| 識別 | ||||||||||||
| 名稱 | 十複合正四面體 | |||||||||||
| 參考索引 | UC6, W25 | |||||||||||
| 鮑爾斯縮寫 | e | |||||||||||
| 性質 | ||||||||||||
| 體 | 10 | |||||||||||
| 面 | 40 | |||||||||||
| 邊 | 60 | |||||||||||
| 頂點 | 20 | |||||||||||
| 歐拉特徵數 | F=40, E=60, V=20 (χ=0) | |||||||||||
| 組成與佈局 | ||||||||||||
| 複合幾何體數量 | 10 | |||||||||||
| 複合幾何體種類 | 10個正四面體 | |||||||||||
| 對稱性 | ||||||||||||
| 對稱群 | 二十面體群 (Ih) | |||||||||||
| 子群 | 手性四面體群 (T) | |||||||||||
| 圖像 | ||||||||||||
| ||||||||||||
性質
十複合正四面體由10個正四面體組成,當中10個正四面體共用20個頂點,因此整個幾何結構總共有40個面、60條邊和20個頂點[4]。其20個頂點的布局與正十二面體相同[5],故複合正四面體也可以視為是正十二面體經過刻面後的結果。[6]同時,這也代表著正十二面體為十複合正四面體的凸包。[3]
十複合正四面體可以視為是五複合正四面體和其手性鏡像的組合。[2]:45另一方面,十複合正四面體的10個正四面體,亦可以兩兩分成一組,每組為二複合四面體。換句話說這個立體也可以視為是5個二複合四面體的複合體。[7]由於十複合正四面體具備此特性,因此十複合正四面體也可以透過將五複合立方體的每個立方體替換成星形八面體來構造。
 右旋五複合正四面體 |
 左旋五複合正四面體 |
 十複合正四面體 |
若將十複合正四面體視為1個星形二十面體,則這個立體由20個六角星面組成,而這些六角星面可以對應到星形二十面體的胞,在杜瓦記號中可以用Ef1表示。[8]
 組成這種星形二十面體的六角星面 |
 杜瓦記號Ef1對應的星狀圖 |
相關多面體
除了正二十面體形式的十複合正四面體外,另有一些其他具備一定對稱性的10個正四面體之複合體。[9]
第二星形二十面體
 | ||
| 類別 | 星形二十面體 收錄於《五十九種二十面體》中 | |
|---|---|---|
| 識別 | ||
| 名稱 | 第二星形二十面體 | |
| 參考索引 | W27, 6/59 | |
| 數學表示法 | ||
| 杜瓦表示法 | F | |
| 組成與佈局 | ||
| 複合幾何體數量 | 11 | |
| 複合幾何體種類 | 10個正四面體 1個第九星形二十面體 | |
| 面的種類 |  | |
| 對稱性 | ||
| 對稱群 | Ih | |
| 圖像 | ||
| ||
第二星形二十面體可以看做是從十複合正四面體的每個五角凹陷處伸出一個五角錐狀尖刺的幾何結構。[2]:47第二星形二十面體是溫尼爾在其著作《多面體模型》中描述的第二種星形二十面體,並編號為W27;同時這個立體有被收錄在哈里·惠勒的論文中[10]。而在《五十九種二十面體》中,這種立體編號為6[8]。
 第九星形二十面體
第九星形二十面體 十複合正四面體
十複合正四面體 第二星形二十面體
第二星形二十面體
第二星形二十面體在杜瓦記號中可以用F來表示,[8]這代表其包含了星形二十面體中的F層的所有胞,即從中間數來的第8個胞、第9個胞和第11個胞。[11]
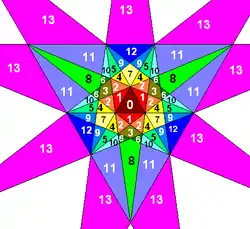 星形二十面體中的胞 |
 第二星形二十面體的胞 |
參見
參考文獻
- Roger Kaufman. . interocitors.com. [2021-09-02]. (原始内容存档于2021-09-02).
- Wenninger, Magnus. . Cambridge University Press. 1974 [2021-09-02]. ISBN 9780521098595. LCCN 69010200. (原始内容存档于2021-08-31).
- Weisstein, Eric W. (编). . at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. (英语).
- Wolfram, Stephen. . from Wolfram Alpha: Computational Knowledge Engine, Wolfram Research (英语).
- Makai Jr, Endre and Tarnai, Tibor. . Elemente der Mathematik. 2021, 76 (1): 1–9.
- Bridge, NJ. . Acta Crystallographica Section A: Crystal Physics, Diffraction, Theoretical and General Crystallography (International Union of Crystallography). 1974, 30 (4): 548–552.
- Brokk. . [2021-09-02]. (原始内容存档于2022-01-15).
- Coxeter, Harold Scott MacDonald; Du Val, P.; Flather, H. T.; Petrie, J. F., 3rd, Tarquin, 1999, ISBN 978-1-899618-32-3, MR 0676126
- Guest, SD. . Periodica Mathematica Hungarica (Springer). 2000, 39 (1): 213–223.
- Wheeler, Albert Harry. . Proc. Internat. Math. Congress, Toronto. 1924, 1: 701–708.
- . mathconsult.ch. [2021-09-02]. (原始内容存档于2021-09-02).
外部連結
- 埃里克·韦斯坦因. . MathWorld.
- VRML model:
- Compounds of 5 and 10 Tetrahedra(页面存档备份,存于) by Sándor Kabai, The Wolfram Demonstrations Project.