变分自编码器
机器学习中,变分自编码器(Variational Autoencoder,VAE)是由Diederik P. Kingma和Max Welling提出的一种人工神经网络结构,属于概率图模式和变分贝叶斯方法。[1]
| 机器学习与 |
|---|
 |
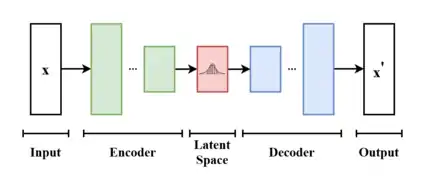
VAE与自编码器模型有关,因为两者在结构上有一定亲和力,但在目标和数学表述上有很大区别。VAE属于概率生成模型(Probabilistic Generative Model),神经网络仅是其中的一个组件,依照功能的不同又可分为编码器和解码器。编码器可将输入变量映射到与变分分布的参数相对应的潜空间(Latent Space),这样便可以产生多个遵循同一分布的不同样本。解码器的功能基本相反,是从潜空间映射回输入空间,以生成数据点。虽然噪声模型的方差可以单独学习而来,但它们通常都是用重参数化技巧(Reparameterization Trick)来训练的。
结构与操作概述
VAE是一个分别具有先验和噪声分布的生成模型,一般用最大期望算法(Expectation-Maximization meta-algorithm)来训练。这样可以优化数据似然的下限,用其它方法很难实现这点,且需要q分布或变分后验。这些q分布通常在一个单独的优化过程中为每个单独数据点设定参数;而VAE则用神经网络作为一种摊销手段来联合优化各个数据点,将数据点本身作为输入,输出变分分布的参数。从一个已知的输入空间映射到低维潜空间,这是一种编码过程,因此这张神经网络也叫“编码器”。
解码器则从潜空间映射回输入空间,如作为噪声分布的平均值。也可以用另一个映射到方差的神经网络,为简单起见一般都省略掉了。这时,方差可以用梯度下降法进行优化。
优化模型常用的两个术语是“重构误差(reconstruction error)”和“KL散度”。它们都来自概率模型的自由能表达式(Free Energy Expression ),因而根据噪声分布和数据的假定先验而有所不同。例如,像IMAGENET这样的标准VAE任务一般都假设具有高斯分布噪声,但二值化的MNIST这样的任务则需要伯努利噪声。自由能表达式中的KL散度使得与p分布重叠的q分布的概率质量最大化,但这样可能导致出现搜寻模态(Mode-Seeking Behaviour)。自由能表达式的剩余部分是“重构”项,需要用采样逼近来计算其期望。[7]
系统阐述
从建立概率模型的角度来看,人们希望用他们选择的参数化概率分布使数据的概率最大化。这一分布常是高斯分布,分别参数化为和,作为指数族的一员很容易作为噪声分布来处理。简单的分布很容易最大化,但如果假设了潜质(latent)的先验分布,可能会产生难以解决的积分。让我们通过对的边缘化找到。
其中,表示可观测数据于下的联合分布,和在潜空间中的形式(也就是编码后的)。根据连锁法则,方程可以改写为
在香草VAE中,通常认为是实数的有限维向量,则是高斯分布。那么便是高斯分布的混合物。
现在,可将输入数据和其在潜空间中的表示的映射定义为
- 先验
- 似然值
- 后验
不幸的是,对的计算十分困难。为了加快计算速度,有必要再引入一个函数,将后验分布近似为
其中是参数化的的实值集合。这有时也被称为“摊销推理”(amortized inference),因为可以通过“投资”找到好的,之后不用积分便可以从快速推断出。
这样,问题就变成了找到一个好的概率自编码器,其中条件似然分布由概率解码器(probabilistic decoder)计算得到,后验分布近似由概率编码器(probabilistic encoder)计算得到。
下面将编码器参数化为,将解码器参数化为。
证据下界(Evidence lower bound,ELBO)
如同每个深度学习问题,为了通过反向传播算法更新神经网络的权重,需要定义一个可微损失函数。
对于VAE,这一思想可以实现为联合优化生成模型参数和,以减少输入输出间的重构误差,并使尽可能接近。重构损失常用均方误差和交叉熵。
作为两个分布之间的距离损失,反向KL散度可以很有效地将挤压到之下。[8][9]
刚刚定义的距离损失可扩展为
现在定义证据下界(Evidence lower bound,ELBO):
使ELBO最大化
等于同时最大化、最小化。即,最大化观测数据似然的对数值,同时最小化近似后验与精确后验的差值。 给出的形式不大方便进行最大化,可以用下面的等价形式:
其中实现为,因为这是在加性常数的前提下得到的东西。也就是说,我们把在上的条件分布建模为以为中心的高斯分布。和的分布通常也被选为高斯分布,因为和可以通过高斯分布的KL散度公式得到:
重参数化

有效搜索到
的典型方法是梯度下降法。 它可以很直接地找到
但是,
不允许将置于期望中,因为出现在概率分布本身之中。重参数化技巧(也被称为随机反向传播[10])则绕过了这个难点。[8][11][12]
最重要的例子是当遵循正态分布时,如。
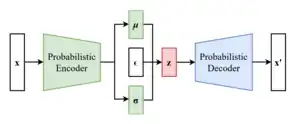 重参数化技巧之后的VAE方案
重参数化技巧之后的VAE方案
可以通过让构成“标准随机数生成器”来实现重参数化,并将构建为。这里,通过科列斯基分解得到:
接着我们有
由此,我们得到了梯度的无偏估计,这就可以应用随机梯度下降法了。 由于我们重参数化了,所以需要找到。令为的概率密度函数,那么
,其中是相对于的雅可比矩阵。由于,这就是
变体
许多VAE的应用和扩展已被用来使其适应其他领域,并提升性能。
-VAE是带加权KL散度的实现,用于自动发现并解释因子化的潜空间形式。这种实现可以对大于1的值强制进行流形分解。这个架构可以在无监督下发现解耦的潜因子。[13][14]
条件性VAE(CVAE)在潜空间中插入标签信息,强制对所学数据进行确定性约束表示(Deterministic Constrained Representation)。[15]
参考
- Pinheiro Cinelli, Lucas; et al. . . Springer. 2021: 111–149. ISBN 978-3-030-70681-4. S2CID 240802776. doi:10.1007/978-3-030-70679-1_5.
- Dilokthanakul, Nat; Mediano, Pedro A. M.; Garnelo, Marta; Lee, Matthew C. H.; Salimbeni, Hugh; Arulkumaran, Kai; Shanahan, Murray. . 2017-01-13. arXiv:1611.02648
 [cs.LG].
[cs.LG]. - Hsu, Wei-Ning; Zhang, Yu; Glass, James. . . December 2017: 16–23 [2023-02-24]. ISBN 978-1-5090-4788-8. S2CID 22681625. arXiv:1707.06265
 . doi:10.1109/ASRU.2017.8268911. (原始内容存档于2021-08-28).
. doi:10.1109/ASRU.2017.8268911. (原始内容存档于2021-08-28). - Ehsan Abbasnejad, M.; Dick, Anthony; van den Hengel, Anton. . 2017: 5888–5897 [2023-02-24]. (原始内容存档于2021-06-24).
- Xu, Weidi; Sun, Haoze; Deng, Chao; Tan, Ying. . Proceedings of the AAAI Conference on Artificial Intelligence. 2017-02-12, 31 (1) [2023-02-24]. S2CID 2060721. doi:10.1609/aaai.v31i1.10966
 . (原始内容存档于2021-06-16) (英语).
. (原始内容存档于2021-06-16) (英语). - Kameoka, Hirokazu; Li, Li; Inoue, Shota; Makino, Shoji. . Neural Computation. 2019-09-01, 31 (9): 1891–1914 [2023-02-24]. PMID 31335290. S2CID 198168155. doi:10.1162/neco_a_01217. (原始内容存档于2021-06-16).
- Kingma, Diederik. . 2013. arXiv:1312.6114
 [stat.ML].
[stat.ML]. - Kingma, Diederik P.; Welling, Max. . 2014-05-01. arXiv:1312.6114
 [stat.ML].
[stat.ML]. - . Lil'Log. 2018-08-12 [2023-02-24]. (原始内容存档于2021-05-14) (英语).
- Rezende, Danilo Jimenez; Mohamed, Shakir; Wierstra, Daan. . International Conference on Machine Learning (PMLR). 2014-06-18: 1278–1286 [2023-02-24]. arXiv:1401.4082
 . (原始内容存档于2023-02-24) (英语).
. (原始内容存档于2023-02-24) (英语). - Bengio, Yoshua; Courville, Aaron; Vincent, Pascal. . IEEE Transactions on Pattern Analysis and Machine Intelligence. 2013, 35 (8): 1798–1828 [2023-02-24]. ISSN 1939-3539. PMID 23787338. S2CID 393948. arXiv:1206.5538
 . doi:10.1109/TPAMI.2013.50. (原始内容存档于2021-06-27).
. doi:10.1109/TPAMI.2013.50. (原始内容存档于2021-06-27). - Kingma, Diederik P.; Rezende, Danilo J.; Mohamed, Shakir; Welling, Max. . 2014-10-31. arXiv:1406.5298
 [cs.LG].
[cs.LG]. - Higgins, Irina; Matthey, Loic; Pal, Arka; Burgess, Christopher; Glorot, Xavier; Botvinick, Matthew; Mohamed, Shakir; Lerchner, Alexander. . 2016-11-04 [2023-02-24]. (原始内容存档于2021-07-20) (英语).
- Burgess, Christopher P.; Higgins, Irina; Pal, Arka; Matthey, Loic; Watters, Nick; Desjardins, Guillaume; Lerchner, Alexander. . 2018-04-10. arXiv:1804.03599
 [stat.ML].
[stat.ML]. - Sohn, Kihyuk; Lee, Honglak; Yan, Xinchen. (PDF). 2015-01-01 [2023-02-24]. (原始内容存档 (PDF)于2021-07-09) (英语).
- Dai, Bin; Wipf, David. . 2019-10-30. arXiv:1903.05789
 [cs.LG].
[cs.LG]. - Dorta, Garoe; Vicente, Sara; Agapito, Lourdes; Campbell, Neill D. F.; Simpson, Ivor. . 2018-07-31. arXiv:1804.01050
 [stat.ML].
[stat.ML]. - Tomczak, Jakub; Welling, Max. . International Conference on Artificial Intelligence and Statistics (PMLR). 2018-03-31: 1214–1223 [2023-02-24]. arXiv:1705.07120
 . (原始内容存档于2021-06-24) (英语).
. (原始内容存档于2021-06-24) (英语). - Razavi, Ali; Oord, Aaron van den; Vinyals, Oriol. . 2019-06-02. arXiv:1906.00446
 [cs.LG].
[cs.LG]. - Larsen, Anders Boesen Lindbo; Sønderby, Søren Kaae; Larochelle, Hugo; Winther, Ole. . International Conference on Machine Learning (PMLR). 2016-06-11: 1558–1566 [2023-02-24]. arXiv:1512.09300
 . (原始内容存档于2021-05-17) (英语).
. (原始内容存档于2021-05-17) (英语). - Bao, Jianmin; Chen, Dong; Wen, Fang; Li, Houqiang; Hua, Gang. . 2017. arXiv:1703.10155
 [cs.CV]. cite arXiv模板填写了不支持的参数 (帮助)
[cs.CV]. cite arXiv模板填写了不支持的参数 (帮助) - Gao, Rui; Hou, Xingsong; Qin, Jie; Chen, Jiaxin; Liu, Li; Zhu, Fan; Zhang, Zhao; Shao, Ling. . IEEE Transactions on Image Processing. 2020, 29: 3665–3680 [2023-02-24]. Bibcode:2020ITIP...29.3665G. ISSN 1941-0042. PMID 31940538. S2CID 210334032. doi:10.1109/TIP.2020.2964429. (原始内容存档于2021-06-28).