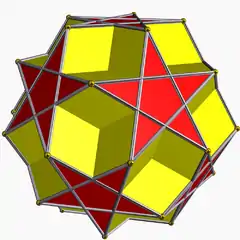
大十二面半二十面體

大十二面半二十面體是一種擬正半多面體[1]，由12個五邊形面和10個穿過整體幾何中心的六邊形面組成，[2]外觀看起來像每個五角星都向內凹陷的截半大十二面體[3]:158。由於其每個面都是正多邊形，且每個頂點對應的角皆相等，因此也可以被歸類為擬正多面體[4]，然而由於這個立體同時具備半多面體的特性，因此被部分學者分成一類新的立體，即擬正半多面體（Versi-Regular Polyhedra），這類立體共有九個，最早在1881年由亞伯特·巴杜羅（）發現並描述[5]。特別地，大十二面半二十面體的外接球的半徑正好是邊長的兩倍。[6]

  提示：此条目页的主题不是大二十面半十二面體、大十二面半十二面體或大十二面截半二十面體。
大十二面半二十面體
大十二面半二十面體
類別均勻星形多面體
半多面體
對偶多面體大十二面半無窮星形二十面體
識別
名稱大十二面半二十面體
Great dodecahemicosahedron
參考索引U65, C81, W102
鮑爾斯縮寫
gidhei
數學表示法
威佐夫符號
5/4 5 | 3（二重覆蓋）
性質
面22
邊60
頂點30
歐拉特徵數F=22, E=60, V=30 （χ=-8）
組成與佈局
面的種類12個正五邊形
10個正六邊形
頂點圖5.6.5/4.6
對稱性
對稱群Ih, [5,3], (*532)
圖像
立體圖
5.6.5/4.6
（頂點圖）

大十二面半無窮星形二十面體
（對偶多面體）

性質

大十二面半二十面體由22個面、60條邊和30個頂點組成[7]，每個頂點都是2個六邊形和2個五邊形的公共頂點，並且呈折四邊形狀排列，在頂點圖中，其可用6, 5/4, 6, 5來表示[8]。

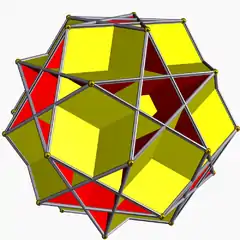
對偶多面體

大十二面半二十面體的對偶多面體為大十二面半無窮星形二十面體[9]。其外觀與小十二面半無窮星形二十面體相同。[10][11]

多面體
大十二面半二十面體
小十二面半二十面體
對偶多面體
大十二面半無窮星形二十面體
小十二面半無窮星形二十面體

相關多面體

大十二面半二十面體與截半大十二面體共用相同的邊排佈方式，因此可以視為是截半大十二面體經過刻面後的結果。[12]此外，小十二面半二十面體、截半大十二面體和大十二面半二十面體皆可以視為截半二十面体的刻面多面體。[13]

參見

參考文獻
  1. David I. McCooey. . dmccooey.com. [2021-09-05]. （原始内容存档于2021-07-30）.
  2. Jonathan Bowers. . polytope.net. 2012 [2021-09-05]. （原始内容存档于2021-09-05）. great dodecahemicosahedron. Symbol is (x^o^'x)/2. Faces are 12 pentagons and 10 central hexagons.
  3. Wenninger, M.J. . Cambridge University Press. 1974 [2021-09-06]. ISBN 9780521098595. LCCN 69010200. （原始内容存档于2021-08-31）.
  4. George W. Hart. . 1996 [2021-09-05]. （原始内容存档于2021-08-30）.
  5. Jean Paul Albert Badoureau. . Journal de l'École polytechnique. 1881, (49): 47-172.
  6. Weisstein, Eric W. (编). . at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. （英语）.
  7. Roman E. Maeder. . mathconsult.ch. MathConsult AG. 1997 [2021-09-05]. （原始内容存档于2020-02-17）.
  8. Conrad, Jonathan and Chamberland, Christopher and Breuckmann, Nikolas P and Terhal, Barbara M. . Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences (The Royal Society Publishing). 2018, 376 (2123).
  9. Magnus Wenninger, , Cambridge University Press, 1983, ISBN 978-0-521-54325-5, MR 0730208 (Page 101, Duals of the (nine) hemipolyhedra)
  10. Weisstein, Eric W. (编). . at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. （英语）.
  11. Weisstein, Eric W. (编). . at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. （英语）.
  12. Richard Klitzing. . 3D convex uniform polyhedra. bendwavy. [2021-09-05]. （原始内容存档于2021-01-26）.
  13. U. Mikloweit. . Polyedergarten. [2021-09-05]. （原始内容存档于2018-11-18）.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.