星形均勻多面體

在幾何學中，星形均勻多面體是指屬於星形多面體的均勻多面體。不包括柱狀均勻多面體，星形均勻多面體共有53種[1]，部分文獻會連同4種星形正多面體共57個立體一併列出[2]。這些多面體皆具有點可遞的特性[3]。

列表

四面體群

頂點布局 (凸包)	非凸
正四面體
截半四面體正八面體	(4.3/2.4.3) 3/2 3 \| 2
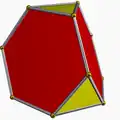截角四面體
小斜方截半四面體 (截半立方體)
大斜方截半四面體 (截角八面體)
扭稜四面體 (正二十面體)

八面體對稱

頂點布局 (凸包)	非凸
立方體
正八面體
截半立方體	(6.4/3.6.4) 4/3 4 \| 3	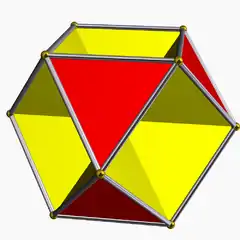(6.3/2.6.3) 3/2 3 \| 3
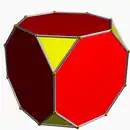截角立方體	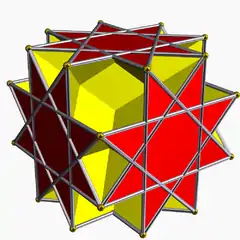(4.8/3.4/3.8/5) 2 4/3 (3/2 4/2) \|	(8/3.3.8/3.4) 3 4 \| 4/3	(4.3/2.4.4) 3/2 4 \| 2
截角八面體
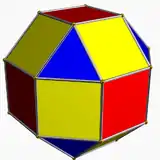小斜方截半立方體	(4.8.4/3.8) 2 4 (3/2 4/2) \|	(8.3/2.8.4) 3/2 4 \| 4	(8/3.8/3.3) 2 3 \| 4/3
大斜方截半立方體	(4.6.8/3) 2 3 4/3 \|
大斜方截半立方體	(8/3.6.8) 3 4 4/3 \|
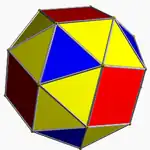扭稜立方體

二十面體對稱

頂點布局 (凸包)	非凸
正二十面體	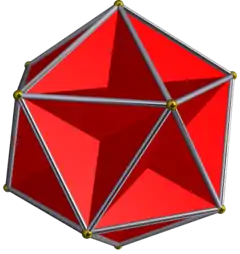{5,5/2}	{5/2,5}	{3,5/2}
截角二十面體 2 5 \|3	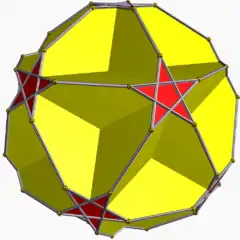U37 2 5/2 \| 5	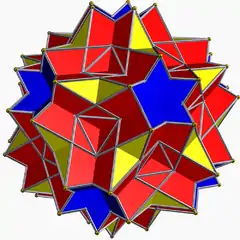U61 5/2 3 \| 5/3	U67 5/3 3 \| 2	U73 2 5/3 (3/2 5/4) \|
截角二十面體 2 5 \|3	U38 5/2 5 \| 2	U44 5/3 5 \| 3	U56 2 3 (5/4 5/2) \|
截角二十面體 2 5 \|3	U32 \| 5/2 3 3
截半二十面體 2 \| 3 5	U49 3/2 3 \| 5	U51 5/4 5 \| 5	U54 2 \| 3 5/2	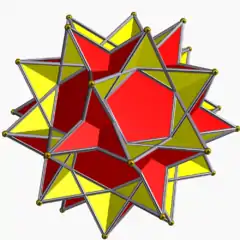U70 5/3 5/2 \| 5/3	U71 3 3 \| 5/3	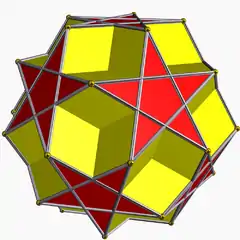U36 2 \| 5 5/2	U62 5/3 5/2 \| 3	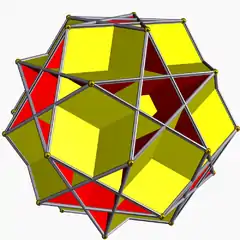U65 5/4 5 \| 3
截角十二面體 2 3 \| 5	U42	U48	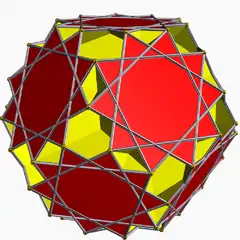U63
截角十二面體	U72
正十二面體	{5/2,3}	U30	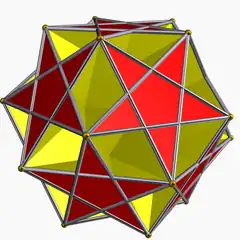U41	U47
小斜方截半二十面体	U33	U39	U58
小斜方截半二十面体	U55
小斜方截半二十面体	U31	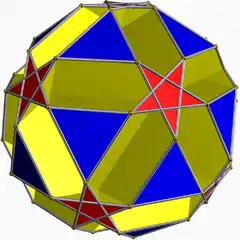U43	U50	U66
小斜方截半二十面体	U75	U64	斯基林圖形
大斜方截半二十面体	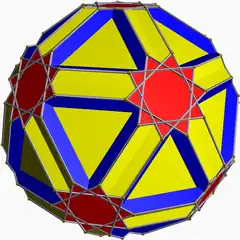U45
大斜方截半二十面体	U59
大斜方截半二十面体	U68
扭稜十二面体	U40	U46	U57	U69	U60	U74

參見

星形多面體

參考文獻

. quantimegroup.com. [2019-09-27]. （原始内容存档于2018-08-31）.
Gérard P. Michon, Ph.D. . [2019-09-27]. （原始内容存档于2020-09-23）.
Coxeter, H. S. M. . Philosophical Transactions of the Royal Society of London. Series A, Mathematical and Physical Sciences. May 13, 1954, 246 (916): 401–450. doi:10.1098/rsta.1954.0003.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.