大斜方十二面體
大斜方十二面體是一種星形均勻多面體,由30個正方形和12個正十角星組成[6],索引為U73,對偶多面體為大菱形十二面六十面體,其外觀與大十二面截半二十面體類似,差別只在正五角星面和三角形面被替換為正方形面,[7]:168並且可以視為是大十二面截半二十面體的刻面多面體[8][9]。
 | ||||
| 類別 | 均勻星形多面體 | |||
|---|---|---|---|---|
| 對偶多面體 | 大菱形十二面六十面體 | |||
| 識別 | ||||
| 名稱 | 大斜方十二面體 great rhombidodecahedron | |||
| 參考索引 | U73, C89, W109 | |||
| 鮑爾斯縮寫 | gird | |||
| 數學表示法 | ||||
| 威佐夫符號 | 2 5/3 (3/2 5/4) | [1] 3/2 5/3 2 |[2][3][4][5] | |||
| 性質 | ||||
| 面 | 42 | |||
| 邊 | 120 | |||
| 頂點 | 60 | |||
| 歐拉特徵數 | F=42, E=120, V=60 (χ=-18) | |||
| 組成與佈局 | ||||
| 面的種類 | 30個正方形(15個{4}和15個{4/3})[5] 12個正十角星(6個{10/3}和6個{10/7})[5] | |||
| 頂點圖 | 4.10/3.4/3.10/7 | |||
| 對稱性 | ||||
| 對稱群 | Ih, [5,3], *532 | |||
| 圖像 | ||||
| ||||
外觀
大斜方十二面體外觀與大十二面截半二十面體類似,其有與大十二面截半二十面體相同的十角星面,只是五角星面和三角形面被替換為正方形面 [7]:168。大斜方十二面體的這些正方形面在對應於大十二面截半二十面體中兩個浮雕五角星的相交處以及三角形面相交有如玫瑰花結的地方有更深的孔[7]:168。在大斜方十二面體的中對應於大十二面截半二十面體中兩個浮雕五角星的相交處有外觀如六面狀的凹陷,這個凹陷處的四個側面為大斜方十二面體的正方形面、底部為兩個大斜方十二面體的十角星面的局部,漏出的部份分別為十角星面中36度和72度的變種等腰三角形[7]:168。
 大斜方十二面體 |
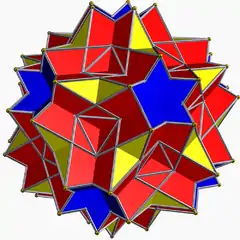 大十二面截半二十面體 |
性質
大斜方十二面體共由42個面、120條邊和60個頂點組成[2][10]。在其42個面中,有30個正方形面和12個十角星面,在這30個正方形面中,有15個是一般的正方形面(施萊夫利符號:{4})和15個是反向相接的正方形面(施萊夫利符號:{4/3});在12個十角星面中,有6個是一般的十角星面(施萊夫利符號:{10/3})和6個是反向相接的十角星面(施萊夫利符號:{10/7})[5]。在其60個頂點中,每個頂點都是2個十角星和2個正方形的公共頂點,且這些面依照十角星、正方形、反向相接的十角星和反向相接的正方形的順序排列,在頂點圖中可以用(10/3.4.10/7.4/3)來表示[11][12]。若將大斜方十二面體作為一個簡單多面體,也就是將自相交的部分分離開來,則這個立體會有612個外部面[12]。大斜方十二面體在威佐夫記號中可以表示為[1]、 2 5/3 (3/2 5/4) |、 3/2 5/3 2 |[2][3][4][5][13]。
相關多面體
大斜方十二面體與截角大十二面體以及6和12複合五角柱共用相同的頂點佈局。同時,其亦與非凸大斜方截半二十面體和大十二面截半二十面體共用相同的邊佈局。[8]
 非凸大斜方截半二十面體 |
 大十二面截半二十面體 |
 大斜方十二面體 |
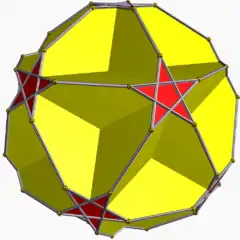 截角大十二面體 |
 六複合五角柱 |
 十二複合五角柱 |
圖像
 傳統填充 |
 相交偶數次為外部 |
參見
- 均勻多面體列表
參考文獻
- Eric W. Weisstein. . archive.lib.msu.edu. 1999-05-25 [2022-08-21]. (原始内容存档于2021-12-05).
- Maeder, Roman. . MathConsult. [2022-08-21]. (原始内容存档于2022-08-21).
- Paul Bourke. . Math Consult AG. October 2004 [2019-09-27]. (原始内容存档于2013-09-02).
- Klitzing, Richard. (PDF). tic. 2002, 2 (4): 3 [2022-08-21]. (原始内容存档 (PDF)于2022-08-14).
- Zvi Har'El. . harel.org.il. 2006-11-14 [2022-08-14]. (原始内容存档于2022-08-23).
- David I. McCooey. . [2022-08-21]. (原始内容存档于2021-09-11).
- Wenninger, M.J. . Cambridge University Press. 1974 [2021-09-05]. ISBN 9780521098595. LCCN 69010200. (原始内容存档于2021-08-31).
- Richard Klitzing. . bendwavy.org. [2022-08-21]. (原始内容存档于2021-11-29).
- Richard Klitzing. . bendwavy.org. [2022-08-21]. (原始内容存档于2022-08-21).
- V.Bulatov. . [2022-08-21]. (原始内容存档于2021-02-28).
- Kovič, J. (PDF). Int. J. Open Problems Compt. Math. 2012, 5 (4) [2022-08-21]. (原始内容存档 (PDF)于2022-08-14).
- Robert Webb. . software3d.com. [2022-08-21]. (原始内容存档于2021-05-11).
- George W. Hart. . [2022-08-21]. (原始内容存档于2018-09-19).
- Weisstein, Eric W. (编). . at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. (英语).
- David I. McCooey. . [2022-08-21]. (原始内容存档于2017-04-20).


