大雙三斜三十二面體

在幾何學中，大雙三斜三十二面體是非凸均勻多面體中的一種星形多面體，其索引編號在均勻多面體中為U47、溫尼爾的多面體模型中為W87[1][2]。大雙三斜三十二面體的對偶多面體為大三角六邊形二十面體[3][4]。

大雙三斜三十二面體
大雙三斜三十二面體
類別均勻星形多面體
對偶多面體大三角六邊形二十面體在维基数据编辑
識別
名稱大雙三斜三十二面體
參考索引U47, C61, W87
鮑爾斯縮寫
gidtid在维基数据编辑
數學表示法
威佐夫符號
3/2 | 3 5
3 | 3/2 5
3 | 3 5/4
3/2 | 3/2 5/4
性質
面32
邊60
頂點20
歐拉特徵數F=32, E=60, V=20 （χ=-8）
組成與佈局
面的種類20個正三角形{3}
12個正五邊形{5}
面的佈局
20{3}+12{5}
頂點圖((3.5)3)/2
對稱性
對稱群Ih, [5,3], *532
圖像

((3.5)3)/2
（頂點圖）

大三角六邊形二十面體
（對偶多面體）

性質

大雙三斜三十二面體共有32個面、60條邊和20個頂點[5][6]，其32個面中包括了20個三角形和12個五邊形。每個頂點都是3個三角形和3個五邊形的公共頂點。

其外接球半徑為倍的邊長[7]，巧合地，立方體的外接球半徑也是倍的邊長。

在施萊夫利符號的擴充表示法中，大雙三斜三十二面體可以用 a{5/2,3} 或c{3,5/2}來表示。在考克斯特記號中也能用label5-4 branch_10ru split2 node 或node_h3 5-2 node 3 node 來表示，其中label5-4 branch_10ru split2 node 與node_h3 5-2 node 3 node 是等價的。

相關多面體
a{5,3} a{5/2,3} b{5,5/2}
label5-2 branch_10ru split2 node  = node_h3 5 node 3 node  label5-4 branch_10ru split2 node  = node_h3 5-2 node 3 node  node 5 node_h3 5-2 node 

小雙三斜三十二面體
大雙三斜三十二面體
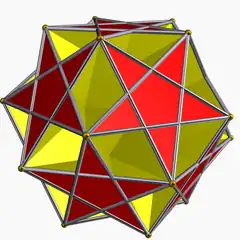雙三斜十二面體

正十二面體 （凸包）
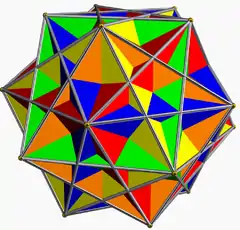五複合立方體

對偶複合體

大三角六邊形二十面體與其對偶的複合體為複合大雙三斜三十二面體大三角六邊形二十面體。其共有52個面、120條邊和52個頂點，其尤拉示性數為-16，虧格為9，有20個非凸面，在威佐夫記號中以(3/2 | 3 5)表示[8]。

參見

參考文獻
  1. Wenninger, Magnus. . Cambridge University Press. 1974. ISBN 0-521-09859-9.
  2. . colinspics.org. [2016-09-01]. （原始内容存档于2016-09-01）.
  3. Eric W. Weisstein. . 密西根州立大學圖書館. [2016-09-01]. （原始内容存档于2014-07-11）.
  4. Weisstein, Eric W. (编). . at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. （英语）.
  5. . bulatov.org. [2016-09-01]. （原始内容存档于2016-03-26）.
  6. . mathconsult. [2016-09-01]. （原始内容存档于2016-03-28）.
  7. Weisstein, Eric W, , Boca Raton: Chapman & Hall/CRC, 2003, ISBN 1-58488-347-2
  8. . bulatov.org. [2016-09-01]. （原始内容存档于2016-03-04）.

外部連結
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.