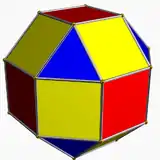
小斜方立方體
小斜方立方體是一種均勻多面體[1],由12個正方形和6個八邊形組成[2],其外觀與小立方立方八面體十分相似,差別在小立方立方八面體的凹陷處在小斜方立方體中是面,而小立方立方八面體的面在小斜方立方體中是凹陷處。[3]:134小斜方立方體最早出現在1881年由亞伯特·巴杜羅()描述的6種半擬正多面體(Versi-Quasi-Regular Polyhedra)中[4]。後來又被考克斯特和米勒於1930年到1932年間發現並命名。[5]此外,小斜方立方體可以視為小斜方截半立方体經過刻面後的結果[6],同時,其凸包也為小斜方截半立方体。[7]
 | ||||
| 類別 | 均勻星形多面體 | |||
|---|---|---|---|---|
| 對偶多面體 | 小反平行四邊形二十四面體 | |||
| 識別 | ||||
| 名稱 | 小斜方立方體 Small rhombihexahedron | |||
| 別名 | 小斜方六面體 | |||
| 參考索引 | U18, C60, W86 | |||
| 鮑爾斯縮寫 | sroh | |||
| 數學表示法 | ||||
| 威佐夫符號 | 2 4 (3/2 4/2) | | |||
| 性質 | ||||
| 面 | 18 | |||
| 邊 | 48 | |||
| 頂點 | 24 | |||
| 歐拉特徵數 | F=18, E=48, V=24 (χ=-6) | |||
| 組成與佈局 | ||||
| 面的種類 | 12個正方形 6個八邊形 | |||
| 頂點圖 | 4.8.4/3.8/7 | |||
| 對稱性 | ||||
| 對稱群 | Oh, [4,3], (*432) | |||
| 圖像 | ||||
| ||||
命名
在名稱中,小斜方立方體的「斜方」(Rhombi-)是指菱形,表示這個多面體有12個面分別與菱形十二面體的12個面平行,這12個面為正方形;小斜方立方體的立方體(-hexahedron)則代表這個立體有6個面分別與立方體(又稱六面體)的6個面平行,這6個面在小斜方立方體中為正八邊形。[8]
性質
小斜方立方體由18個面、48條邊和24個頂點組成[8][2][9],其中24個頂點互相交叉連結交,沒有交叉連結的部分構成了小斜方立方體的12個正方形面,[10]並且這12個正方形面分別與菱形十二面體的12個菱形面平行[8];剩下的交叉連結的頂點構成了6個八邊形,這6個八邊形面分別與立方體的6個正方形面平行。[8]同時,這24個頂點具有點可遞的特性,這意味著,這立體上的任意兩個頂角A和B,透過旋轉或鏡射這個立體,使A移動到B原來的位置時,其頂角以及其二面角仍然佔據了相同的空間區域[11],也代表著這個立體是一個等角立體。小斜方立方體每個頂點都是2個八邊形和2個正方形的公共頂點,並具有交叉梯形的頂點圖[11]在頂點布局中,可以用{8, 4, 8/7, 4/3}來表示[9][12]。若將這個立體視為簡單多面體,則其由66個面組成[8]
相關多面體
小斜方立方體與星形截角立方體共用相同的頂點布局[14],其亦與大斜方立方體、小立方立方八面體和小斜方截半立方体有著相同的稜布局。[7]

 小斜方立方體
小斜方立方體 星形截角立方體
星形截角立方體
小斜方立方體與大斜方立方體拓樸同構,其可以透過替換八邊形與八角星來轉變為另一個立體。[7][15]
 小斜方立方體
小斜方立方體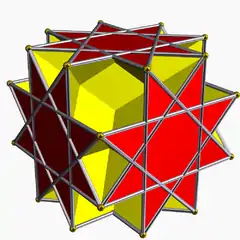
參見
參考文獻
- Wolfram, Stephen. . from Wolfram Alpha: Computational Knowledge Engine, Wolfram Research (英语).
- Vladimir Bulatov. . Polyhedra Collection. [2021-09-12]. (原始内容存档于2021-09-03).
- Wenninger, M.J. . Cambridge University Press. 1974 [2021-09-05]. ISBN 9780521098595. LCCN 69010200. (原始内容存档于2021-08-31).
- Jean Paul Albert Badoureau. . Journal de l'École polytechnique. 1881, (49): 47-172.
- H. S. M. Coxeter; M. S. Longuet-Higgins; J. C. P. Miller. . Philosophical Transactions of the Royal Society of London. Series A. Mathematical and Physical Sciences. 1954, 246: 401–450.
- Weisstein, Eric W. (编). . at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. (英语).
- Klitzing, Richard. . bendwavy.org. [2021-09-12]. (原始内容存档于2021-08-09).
- Robert Webb. . software3d.com. [2021-09-12]. (原始内容存档于2021-03-02).
- Roman E. Maeder. . mathconsult.ch. 1997 [2021-09-12]. (原始内容存档于2020-02-17).
- Wenge Qiu, Jason A. Perman, Łukasz Wojtas, Mohamed Eddaoudi, Michael J. Zaworotko. . Chemical Communications. 2010, 46 (46): 8734 [2021-09-12]. ISSN 1359-7345. doi:10.1039/c0cc03270k (英语).
- David I. McCooey. . dmccooey.com. [2021-09-05]. (原始内容存档于2020-06-18).
- Paul Bourke. . paulbourke.net. October 2004 [2021-09-12]. (原始内容存档于2013-09-02).
- David I. McCooey. . dmccooey.com. [2021-09-05]. (原始内容存档于2021-09-03).
- Klitzing, Richard. . bendwavy.org. [2021-09-12]. (原始内容存档于2021-08-09).
- Klitzing, Richard. . bendwavy.org. [2021-09-05]. (原始内容存档于2021-08-09).


