矛盾
在傳統邏輯學中,如果一個命題與自身或既定事實相衝突,則稱之為矛盾(英語:,又稱恆假)。這種情況經常用來發現人們的不誠實信念或偏見。亞里士多德提出的無矛盾律,進一步說明了應用邏輯的普遍原則,即一件事物不可能在同一時間對於相同的對象同時為是與非[1]。
在當代的形式邏輯和類型論領域,「矛盾」一詞專指某個特定的命題,通常使用偽符號()來表示。根據邏輯規則,如果一個命題能導出「假」,則該命題被視為矛盾,亦即它是一個永遠不成立的命題(也就是說,自我矛盾的論述)[2][3]。這個概念可以延伸應用到一系列的論述上,這時可以說這一系列論述中「包含有」矛盾。
词源
汉语辞源出自《韩非子》中《难一》所述故事:
| 楚人有鬻盾与矛者,誉之曰:“吾盾之坚,物莫能陷之。”以誉其矛曰:“吾矛之利,于物无不陷也。”或曰:“以子之矛陷子之盾,何如?”其人弗能应也。夫不可陷之盾与无不陷之矛,不可同世而立。 |
白話文大意為:有一位賣盾牌和賣矛的楚國人,他讚譽自己賣的盾牌說:“我的盾牌堅固無比,任何物件都無法刺穿它。”又誇讚自己賣的矛說:“我的矛鋒利無比,於任何物件都可以刺穿。”有人問他說:“用你的矛来試著刺你的盾,將會如何?”其人一句話都無法回應。不能被刺穿的盾牌和能刺穿一切的矛,是不可以同时存在。
邏輯學上的矛盾
逻辑学上,矛盾、自相矛盾或牴觸(contradiction)被更加特殊化的定义为同时断言一个命題和它的否定。这个想法基于亚里士多德的无矛盾律,它声称「你不能同时声称某事物在同一方面既是又不是」。
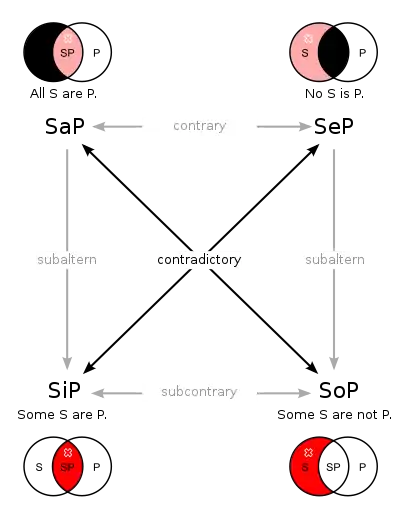
當我們說命題S與P矛盾時,意思是二者相當於A和非A的關係,也就是S與P不能同時為真、亦不能同時為假。
舉例來說:「所有學生都用功」和「有些學生不用功」就是在邏輯上矛盾;另一個例子是「死刑已被廢除,嚴格禁止包括謀殺在內的任何罪行使用死刑;但為了受害者著想及平衡各方意見,若謀殺受害者家屬強烈主張兇手必須以死謝罪,政府有義務協助受害者家屬以最快的速度讓罪犯接受死亡」,在其中「死刑已被廢除」代表的就是「這個國家沒有死刑」,而「若謀殺受害者家屬強烈主張兇手必須以死謝罪,政府有義務協助受害者家屬以最快的速度讓罪犯接受死亡」則指向「這個國家有死刑」這點,顯然一個國家或地區不可能同時有死刑又沒有死刑,此種法律是自相矛盾。
習慣上說的矛盾其實是指邏輯學上的不一致,矛盾必然不一致,然而不一致不必然矛盾。
利用矛盾的证明
在演绎逻辑和数学中,矛盾通常作为有什么东西错误了的迹象,你需要折回你的推理的步骤并"检查你的前提"。这在数学中的反证法中发挥了巨大的作用:因为矛盾永远不能为真,所以它永远不能是有着全部为真的前提的有效论证的结论。要构造一个利用矛盾的证明,你需要从一组前提构造一个有效的论证,得出是逻辑矛盾的一个结论。因为结论为假,并且论证是有效的,唯一的可能性是一个或多个前提为假。在很多关键的数学证明中使用了这种方法,比如欧几里得对没有最大素数的证明,和康托尔对在0和1之间有不可数個实数的对角线证明。
涉及矛盾的悖论
矛盾同许多有名的悖论有关。其中之一是在一阶谓词演算中从矛盾中可以推导出任何命题(也叫陈述)。换句话说,依据谓词演算,不管P和Q意味着什么,如果P和¬P都为真的,则Q为真。在这个事实的表达中,矛盾被称为在一阶逻辑中的"逻辑爆炸"。
例如,下列论证是严格有效,就是说前提在逻辑上蕴涵结论:
下面的论证也是有效的:
- 前提: 5既是偶数又是奇数。(就是P ∧ ¬P)。
- 结论:神不存在。(就是¬Q)。
注意这两个论证共有的前提是错误的;5是奇数而不是偶数。所以此等论证都不是可靠,这意味着它们都没有为信赖它的结论给出一个逻辑基础。
可能大多数人认为这是怪异的,如果5既是偶数又是奇数,就能够在逻辑上得出明显的不相关的任何事情比如 神的存在性的结论。更加怪异的是,这个悖论还蕴涵了,如果一个人有是矛盾的任何两个信仰,则这个人在逻辑上证实任何可想像到的信仰。