数学模型

首先必須明白問題的本質，才能將之轉換成操作定義和數學符號。根據已知資訊的多寡，模型可以分為三類：

1. 白箱模型：指那些内部规律比较清楚的模型。如力学、热学、电学以及相关的工程技术问题[5]。
2. 灰箱模型：指那些内部规律尚不十分清楚，在建立和改善模型方面都还不同程度地有许多工作要做的问题。如气象学、生态学、经济学等领域的模型[6]。
3. 黑箱模型：指一些其内部规律还很少为人们所知的现象。如生命科学、社会科学等方面的问题。但由于因素众多、关系复杂，也可简化为灰箱模型来研究[7]。

模型描述的是理想化的情境，如 George E. P. Box 所言：「所有的模型都是錯的，但有些很有用」。判斷哪些核心部件必須保留、哪些可以簡化是建模的重要步驟。如果所有的細節都包含在內，模型和真實世界是一樣的，則沒有使用模型的意義。

物理中常用的若干简化模型包括无质量的绳子、点粒子、理想氣體以及無限深方形阱[8]。用简单方程表示的物理定律有牛顿定律、馬克士威方程組和薛定谔方程等[9]。这些定律都是建立在实际情况的数学模型基础上的。许多实际情况是非常复杂的，因此要用电脑进行模拟，计算可行的模型是建立在基本定律或基本定律的近似模型上的。例如，分子可以用薛定谔方程的近似解分子轨道模型进行模拟。在工程中，物理模型通常运用的数学方法如有限元分析[10]。不同数学模型使用不同的几何学，但所使用的不一定是描述宇宙最准确的几何学。欧几里得几何多用在经典物理学中，而狭义相对论和廣義相對論都是不使用欧几里得几何的理论[11]。

在數理生物學中，哈溫定律描述一個無限大的族群、裡面隨機交配、沒有天擇或突變。族群遺傳學模型常假設固定的族群大小。計量遺傳學模型則假設連續性狀。

決定实际问题中的各种因素，轉換為变量表示。接著應分析这些变量之间的关系，哪些是相互依存的，哪些是独立的，他们具有什么样的关系，用合理的數學式表示這些關係。根据实际问题选用合适的数学框架（典型的有优化问题，配置问题等等），并具体的应用问题在这个数学框架下表出，並用合适的算法求解数学框架下表出的问题。在這個過程中可能用到计算机模拟和编程，常用的数学工具软件包括MATLAB和Mathematica。

最後使用计算结果解释实际问题，并且分析结果的可靠性。這時常需用到各種信息可視化的技巧。

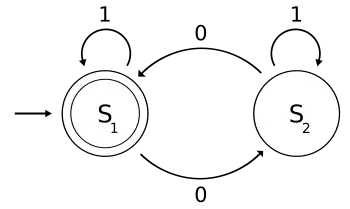
• 计算机科学中的一个常见模型是各种自动机，如用抽象数学概念定义的确定有限状态自动机（DFA），但是由于DFA的确定性性质，可以用硬件或软件来实现以解决各种具体问题。
• 许多日常活动都暗含着数学模型的运用。把地球的一个区域投影在小的地图平面上就是一个模型，[15] 该模型可以用来规划旅行。
• 人口增長：一個簡單（但粗略）的人口增長模型為马尔萨斯增长模式；另一個較理想且被大量使用的人口增長模型為逻辑函数和其延伸[5]。
• 位能場中的粒子模型：在此模型中，粒子被視為一個質量為m的點，其軌跡為一將時間映射至其空間座標的函數x : R → R³，位能場由一函數V:R³ → R給定，則其軌跡為如下微分方程的解：

${\displaystyle -{\frac {\mathrm {d} ^{2}\mathbf {r} (t)}{\mathrm {d} t^{2}}}m={\frac {\partial V[\mathbf {r} (t)]}{\partial x}}\mathbf {\hat {x}} +{\frac {\partial V[\mathbf {r} (t)]}{\partial y}}\mathbf {\hat {y}} +{\frac {\partial V[\mathbf {r} (t)]}{\partial z}}\mathbf {\hat {z}} ,}$

也可以写作

${\displaystyle m{\frac {\mathrm {d} ^{2}\mathbf {r} (t)}{\mathrm {d} t^{2}}}=-\nabla V[\mathbf {r} (t)].}$

需注意此模型假定粒子為一質點，但這在許多情形之下是錯誤的，如行星運動的模型之類。

• 邻居遥感模型解释了从最初的混沌真菌网络形成蘑菇的过程。
• 计算机科学：计算机网络模型，数据模型，表面模型等。
• 力学：火箭模型运动等。

MCM/ICM是Mathematical Contest in Modeling和Interdisciplinary Contest in Modeling的缩写，即“数学建模竞赛”和“交叉学科建模竞赛”。MCM始于1985年，ICM始于2000年，由COMAP（the Consortium for Mathematics and Its Application，美国数学及其应用联合会）主办，得到了SIAM，NSA，INFORMS等多个组织的赞助。MCM/ICM与其他著名数学竞赛（如Putnam数学竞赛）的区别在于其着重强调研究问题、解决方案的原创性、团队合作、交流以及结果的合理性。竞赛以三人（本科生）为一组，在四天时间内，就指定的问题完成从建立模型、求解、验证到论文撰写的全部工作。竞赛每年都吸引大量著名高校参赛。2008年MCM/ICM有超过2000个队伍参加，遍及五大洲。MCM/ICM已经成为最著名的国际大学生竞赛之一。

全国大学生数学建模竞赛创办于1992年，每年一届，是首批列入“高校学科竞赛排行榜”的19项竞赛之一。2020年，来自全国及美国、英国、马来西亚的1470所院校/校区、45680队(本科41826队、专科3854队)、13万多人报名参赛[16]。

• Aris, Rutherford [ 1978 ] ( 1994 ). Mathematical Modelling Techniques, New York: Dover. ISBN 978-0-486-68131-3
• Bender, E.A. [ 1978 ] ( 2000 ). An Introduction to Mathematical Modeling, New York: Dover. ISBN 978-0-486-41180-4
• Gershenfeld, N. (1998) The Nature of Mathematical Modeling, Cambridge University Press ISBN 978-0-521-57095-4 .
• Lin, C.C. & Segel, L.A. ( 1988 ). Mathematics Applied to Deterministic Problems in the Natural Sciences, Philadelphia: SIAM. ISBN 978-0-89871-229-2