正多邊形多面體
正多邊形多面體又稱為正多邊形面多面體()是指所有面皆由正多邊形組成的多面體,其每面的邊數不一定相等,也不一定點可遞,也無對稱要求,因此正多邊形多面體不一定有外接球。 所有側面為正方形的棱柱體和側面為正三角形的反棱柱都屬於正多邊形多面體,在正多邊形多面體的研究通常都是探討棱柱體和反棱柱等柱狀均勻多面體以外的正多邊形多面體。 凸正多邊形多面體包括柏拉圖立體、半正多面體和詹森多面體,非凸正多邊形多面體除了包括星形正多面體、星形均勻多面體、星形柱狀均勻多面體外,還包括無窮多種可能的多面體組合和一些自相交的多面體,如側錐七角柱和魯洛夫斯的星形三十面體。
| 部分的正多邊形多面體 | |
|---|---|
 正十二面體 |
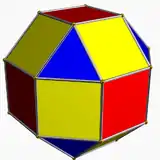 小斜方截半立方体 |
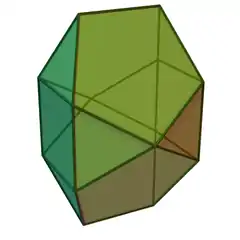 雙新月雙罩帳 |
 五角星柱 |
分類
正多邊形多面體可粗略分成下列幾類:[1]
| 凸多面體 | 等面[註 2] | 等角 | 種類 | 數量 |
|---|---|---|---|---|
| 是 | 是 | 是 | 凸正多面體(柏拉圖立體) | 5 |
| 是 | 是 | 否 | 凸正三角面多面體(正四面體、正八面體、正二十面體除外,因為此三者為柏拉圖立體,是等角圖形) | 5(凸正三角面多面體有8個[2],但是扣掉3個[註 3]) |
| 是 | 否 | 是 | 正角柱、正反角柱 | ∞ |
| 阿基米德立體 | 13 | |||
| 是 | 否 | 否 | 詹森多面體(J12、J13、J17、J51、J84除外,此五者為三角面多面體,所有面全等[註 2]) | 87(詹森多面體有92個,但是扣掉5個[註 4]) |
| 否 | 是 | 是 | 星形正多面體(克卜勒-龐索立體) | 4 |
| 否 | 是 | 否 | 非凸正三角面多面體(含多連正四面體)、多連立方體(正方形面不共面的情況)、多連正十二面體 | ∞ |
| 否 | 否 | 是 | 正星形柱、正星形反柱(皆屬於柱狀均勻多面體) | ∞ |
| 星形均勻多面體 | 53[3] | |||
| 否 | 否 | 否 | 其他由正多邊形組成的非凸多面體(例如側錐七角柱) | ∞ |
凸正多邊形多面體
凸正多邊形多面體是指所有面皆由正多邊形組成的凸多面體,包括了無窮多種的棱柱體和反棱柱、柏拉圖立體、阿基米德立體和詹森多面體。一般對於凸正多邊形多面體的研究通常不討論無窮集合的棱柱體和反棱柱,不包括棱柱體和反棱柱的話,凸正多邊形多面體共有110個[4],若嚴格不計棱柱體與反棱柱,則立方體(正四角柱)和正八面體(正三角反棱柱)不算,共108個[4];有些文獻會將除了柏拉圖立體、阿基米德立體和詹森多面體外的邊數最少之棱柱體和反棱柱也列入(正三角柱和正四角反棱柱)共有112個。[5]柏拉圖立體與阿基米德立體早在公元前就已發現,而詹森多面體則發現得較晚,由諾曼·詹森在1966年發現並命名,並由維克托·查加勒在1969年證明諾曼·詹森所列出的立體是完整的,沒其其他更多立體有此特性,至此,嚴格凸的正多邊形多面體研究已算完備。[4]
有n面的凸正多邊形多面體的個數為(從n=1開始):
- 0、0、0、1、2、3、2、7、3、6、4、7、3、13、2、5、4、6、1、9、2、6、1、4、1、8、4、2、1、3、1、10、1、3、1、2、4、3、1、2、1、9、1、2、1、2、2、2、1、2、1、9、1、2、1、2、1、2、1、2、1、9、1、2、... (OEIS數列A180916)
有n個頂點的凸正多邊形多面體的個數為(從n=1開始):
非嚴格凸正多邊形多面體
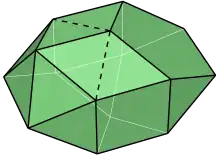
非嚴格凸正多邊形多面體則表示該多面體可能有相共面的面。若未予任何限制條件,則這類立體有無限多種;但若限制所有頂點都要嚴格位於邊界頂角處,不得位於面的邊上或內部,則滿足條件的立體還有78個。這78個的前6個由B·A·伊万諾夫()[6]和普里亞欣·尤·A()[7]分別於1971年和1973年發現,而亞歷克斯·多斯基()[8]、羅傑·考夫曼()和史蒂夫·沃特曼()[9]在2006年發現了另外70個這類立體,完整的這些立體由維克多·扎加勒()[10]和阿列克謝·維克多羅維奇·蒂莫芬科()[11]獨立列出,並由蒂莫芬科於2010年證明這列表完整[11][12][13]。
而無此條件限制的立體雖有無限多種,但仍可加以分類,並可分類成有限種類別。[14]這些分類由蒂莫芬科和他的學生完成[15][4]。
非凸正多邊形多面體
非凸正多邊形多面體有無限多種,其中經常研究探討星形均勻多面體,所有星形均勻多面體皆是非凸正多邊形多面體,但星形均勻多面體通常有自相交的面。無自相交面的非凸正多邊形多面體亦有無限多種,目前尚未有系統分類。邦妮·斯圖爾特(Bonnie Stewart)在其著作《環形體歷險記》(Adventures among the Toroids)中探討了關於環形多面體的非凸正多邊形多面體。[16][4]
相關幾何體
凸正多邊形多胞體
凸正多邊形多胞體(convex regular-faced polytope,簡稱CRF polytope)是指所有二維面都是正多邊形的多胞體[17],可以視為是凸正多邊形多面體在高維空間的類比。[18]
布蘭德多胞形
布蘭德多胞形是指所有胞都是正多胞形的正多胞形,也可以視為凸正多邊形多面體在高維空間的類比,由羅絲薇莎·布蘭德於1979年提出。[19]
註釋
參考文獻
- Tom Gettys. . comcast.net. [2022-07-17]. (原始内容存档于2014-04-18).
- Freudenthal, H; van der Waerden, B. L., , Simon Stevin, 1947, 25: 115–128 (荷兰语)(其表明只有8個凸正三角面多面體)
- . quantimegroup.com. [2019-09-27]. (原始内容存档于2018-08-31).
- Robert R Tupelo-Schneck. . [2023-02-04]. (原始内容存档于2022-11-14).
- Martin Berman. . Journal of the Franklin Institute. 1971-05, 291 (5): 329–336 [2023-02-04]. doi:10.1016/0016-0032(71)90071-8. (原始内容存档于2018-06-24) (英语).
- Ivanov, B. A. . Ukrainskiĭ Geometricheskiĭ Sbornik. 1971, 10: 20–34. ISSN 0135-6992 (俄语).
- Prjahin, Ju. A. . Ukrainskiĭ Geometricheskiĭ Sbornik. 1973, (No. 14): 83–88 (俄语).
- Alex Doskey. . [2023-02-04]. (原始内容存档于2023-01-31).
- Steve Waterman. . [2023-02-04]. (原始内容存档于2023-01-31).
- Gurin, AM and Zalgaller, VA. . Translations of the American Mathematical Society-Series 2. 2009, 228: 169.
- Timofeenko, Aleksei Victorovich. . Algebra i Analiz (St. Petersburg Department of Steklov Institute of Mathematics, Russian~…). 2009, 21 (3): 165–209.
- Timofeenko, Aleksei Victorovich. . St. Petersburg Mathematical Journal. 2012-08-01, 23 (4): 779–780 [2023-01-31]. ISSN 1061-0022. doi:10.1090/S1061-0022-2012-01217-3 (英语).
- Robert R Tupelo-Schneck. . [2023-02-04]. (原始内容存档于2021-08-18).
- Yu. A. Pryakhin. . Journal of Soviet Mathematics. 1978-09, 10 (3): 486–487 [2023-02-04]. ISSN 0090-4104. doi:10.1007/BF01476855 (英语).
- A. V. Timofeenko. . Doklady Mathematics. 2009-10, 80 (2): 720–723 [2023-02-04]. ISSN 1064-5624. doi:10.1134/S1064562409050238 (英语).
- Bonnie M. Stewart. 2nd. 1980.
- Richard Klitzing. . bendwavy.org. [2023-02-04]. (原始内容存档于2023-04-11).
- . qfbox.info. [2023-02-04]. (原始内容存档于2023-03-19).
- Richard Klitzing. . bendwavy.org. [2023-02-04]. (原始内容存档于2023-04-11).