注意力机制

假设我们有一个以索引${\displaystyle i}$排列的标记（token）序列。对于每一个标记${\displaystyle i}$，神经网络计算出一个相应的满足${\displaystyle \sum _{i}w_{i}=1}$的非负软权重${\displaystyle w_{i}}$。每个标记都对应一个由词嵌入得到的向量${\displaystyle v_{i}}$。加权平均${\displaystyle \sum _{i}w_{i}v_{i}}$即是注意力机制的输出结果。

可以使用查询-键机制（query-key mechanism）计算软权重。从每个标记的词嵌入，我们计算其对应的查询向量${\displaystyle q_{i}}$和键向量${\displaystyle k_{i}}$。再计算点积${\displaystyle q_{i}k_{j}}$的softmax函数便可以得到对应的权重，其中${\displaystyle i}$代表当前标记、${\displaystyle j}$表示与当前标记产生注意力关系的标记。

某些架构中会采用多头注意力机制（multi-head attention），其中每一部分都有独立的查询（query）、键（key）和值（value）。

下图展示了将英语翻译成法语的机器，其基本架构为编码器-解码器结构，另外再加上了一个注意力单元。在图示的简单情况下，注意力单元只是循环层状态的点积计算，并不需要训练。但在实践中，注意力单元由需要训练的三个完全连接的神经网络层组成。这 三层分别被称为查询（query）、键（key）和值（value）。

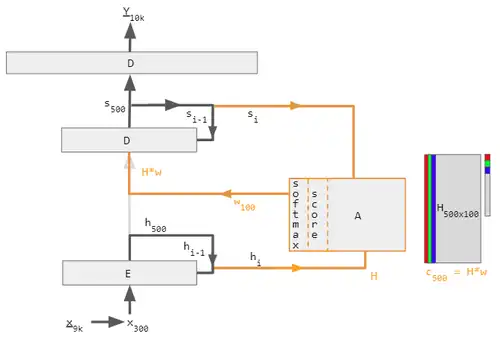加入注意力机制的编码器-解码器架构。图中使用具体的数值表示向量的大小，使其更为直观。左侧黑色箭头表示的是编码器-解码器，中间橘色箭头表示的是注意力单元，右侧灰色与彩色方块表示的是计算的数据。矩阵H与向量w中的灰色区域表示零值。数值下标表示向量大小。字母下标i与i-1表示计算步。

图例 标签 描述 100 语句最大长度 300 嵌入尺寸（词维度） 500 隐向量长度 9k, 10k 输入、输出语言的词典大小 x, Y 大小为9k与10k的独热词典向量。x → x以查找表实现。Y是解码器D线性输出的argmax值。 x 大小为300的词嵌入向量，通常使用GloVe或word2vec等模型预先计算得到的结果。 h 大小为500的编码器隐向量。对于每一计算步，该向量包含了之前所有出现过的词语的信息。最终得到的h可以被看作是一个“句”向量，杰弗里·辛顿则称之为“思维向量”（thought vector）。 s 大小为500的解码器隐向量。 E 500个神经元的循环神经网络编码器。输出大小为500。输入大小为800，其中300为词嵌入维度，500为循环连接。编码器仅在初始化时直接连接到解码器，故箭头以淡灰色表示。 D 两层解码器。循环层有500个神经元，线性全连接层则有10k个神经元（目标词典大小）。[7]单线性层就包含500万（500×10k）个参数，约为循环层参数的10倍。 score 大小为100的对准分数 w 大小为100的注意力权重向量。这些权重为“软”权重，即可以在前向传播时改变，而非只在训练阶段改变的神经元权重。 A 注意力模块，可以是循环状态的点积，也可以是查询-键-值全连接层。输出是大小为100的向量w。 H 500×100的矩阵，即100个隐向量h连接而成的矩阵。 c 大小为500的上下文向量 = H * w，即以w对所有h向量取加权平均。

下表是每一步计算的示例。为清楚起见，表中使用了具体的数值或图形而非字母表示向量与矩阵。嵌套的图形代表了每个h都包含之前所有单词的历史记录。在这里，我们引入注意力分数以得到所需的注意力权重。

步	x	h, H = 编码器输出 大小为500×1的向量，以图形表示	s = 解码器提供给注意力单元的输入	对准分数	w = 注意力权重 = softmax(分数)	c = 上下文向量 = H*w	y = 解码器输出
1	I	= “I”的向量编码	-	-	-	-	-
2	love	= “I love”的向量编码	-	-	-	-	-
3	you	= “I love you”的向量编码	-	-	-	-	-
4	-	-	解码器尚未初始化，故使用编码器输出h3对其初始化	[.63 -3.2 -2.5 .5 .5 ...]	[.94 .02 .04 0 0 ...]	.94 * + .02 * + .04 *	je
5	-	-	s4	[-1.5 -3.9 .57 .5 .5 ...]	[.11 .01 .88 0 0 ...]	.11 * + .01 * + .88 *	t'
6	-	-	s5	[-2.8 .64 -3.2 .5 .5 ...]	[.03 .95 .02 0 0 ...]	.03 * + .95 * + .02 *	aime

以矩阵展示的注意力权重表现了网络如何根据上下文调整其关注点。

对注意力权重的这种展现方式回应了人们经常用来批评神经网络的可解释性问题。对于一个只作逐字翻译而不考虑词序的网络，其注意力权重矩阵会是一个对角占优矩阵。这里非对角占优的特性表明注意力机制能捕捉到更为细微的特征。在第一次通过解码器时，94%的注意力权重在第一个英文单词“I”上，因此网络的输出为对应的法语单词“je”（我）。而在第二次通过解码器时，此时88%的注意力权重在第三个英文单词“you”上，因此网络输出了对应的法语“t'”（你）。最后一遍时，95%的注意力权重在第二个英文单词“love”上，所以网络最后输出的是法语单词“aime”（爱）。

注意力机制有许多变体：点积注意力(dot-product attention）、QKV注意力（query-key-value attention）、强注意力（hard attention）、软注意力（soft attention）、自注意力（self attention）、交叉注意力（cross attention）、Luong注意力、Bahdanau注意力等。这些变体重新组合编码器端的输入，以将注意力效果重新分配到每个目标输出。通常而言，由点积得到的相关式矩阵提供了重新加权系数（参见图例）。

1. 编码器-解码器点积	2. 编解码器QKV	3. 编码器点积	4. 编码器QKV	5. Pytorch示例
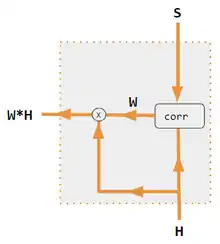同时需要编码器与解码器来计算注意力。[8]	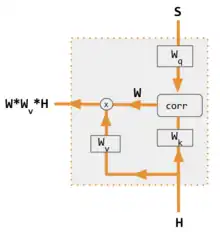同时需要编码器与解码器来计算注意力。[9]	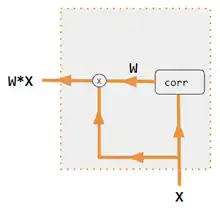解码器不用于计算注意力。因为只有一个输入，W是自相关点积，即w ij = x i * x j。[10]	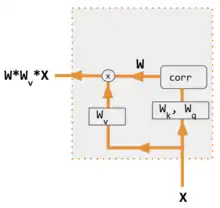解码器不用于计算注意力。[11]	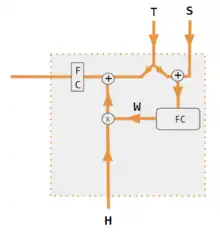使用FC层而非相关性点积计算注意力。[12]