光速

光速，指光在真空中的速率，是一個物理常數，一般記作c，精確值為299792458m/s（有时会取为3.00×108 m/s）。這一數值之所以是精確值，是因為公尺的定義本身就是基於光速和國際時間標準的[1]，任何对光速更精确的测定，都不会改变光速的精确值，相反地，将会使得人们对一米的定义更为精确。

圖中所示：太陽與地球間距離為1.5億公里，此為近似的平均值。示意圖按比例繪出。
光從離開太陽表面算起，需大約8分17秒就能到達地球。
精確值
米每秒299792458
普朗克長度每普朗克時間
（即普朗克單位制）		1
近似值（準確至三個有效位數）
公里每小時10.80亿（1.08×109）[注 1]
英里每秒186000
英里每小時6.71亿（6.71×108）
天文單位每天173[注 2]
光信號傳遞時間近似值
長度時間
1英尺1.0 ns
1米3.3 ns
從地球靜止軌道至地球119 ms
地球赤道長度134 ms
從月球至地球1.3 s
從太陽至地球（1 AU）8.3 分鐘
1光年1.0年
1秒差距3.26年
從最近恒星至太陽（1.3 pc）4.2年
從最近星系（大犬座矮星系）至地球25000 年
橫跨銀河系100000 年
從仙女座星系至地球250萬年
從地球至可見宇宙的邊緣465億年

根據狹義相對論，光速是宇宙中所有的物質運動、訊息傳播的速度上限，也是所有無質量粒子及對應的場波動在真空中運行的速度。這一速度獨立於射源運動以及觀測者所身處的慣性參考系。

數值、記法及單位

真空中的光速通常以小寫c表示，即英文中「」（恒等、常數）或拉丁文「」（迅捷）的首字母。最初，人們曾以詹姆斯·克拉克·馬克士威於1865年使用的符號V表示光速。1856年，威廉·愛德華·韋伯和魯道夫·科爾勞施曾使用c代表另一個常數。該常數後來被證明為光速的倍。1894年，保羅·德汝德重新將c定義為光速。阿爾伯特·愛因斯坦在1905年發表有關狹義相對論的最早德文論文中使用V，但在1907年便轉用當時已通用的符號c。[2][3]

在某些情況下，c表示任何媒介中波傳播的速度，而c0則表示光在真空中的速度[4]。這種使用下標的記法受SI官方出版物認可[5]，且與其它相關常數的記法相符，包括真空磁導率μ0、真空電容率ε0（又稱電常數）以及自由空間阻抗Z0。本條目以c代表真空中的光速。

自1983年起，國際單位制（）將米定義為1⁄299792458秒內光在真空中所運行的距離。因此，光速的精確值等於299792458 m/s[6][7][8]。光速是一個具有量綱的物理常數，因此c的數值取決於所用的單位制[注 3]。在相對論等經常用到c的物理學範疇中，不少文獻會使用自然單位制或幾何化單位制。在這些單位制中，c = 1[10][11]。這樣，公式和計算當中就不會出現c，因為乘以或者除以1並不會對結果有任何的影響。

在物理學中的基礎地位
参见：狹義相對論入門和狹義相對論

光在真空中的傳播速度獨立於波源的運動及觀測者的慣性參考系。[注 4]1865年，詹姆斯·克拉克·馬克士威提出光是一種電磁波，因此必須以他的電磁理論中所出現的速度c傳播。在麥克斯韋電磁理論的推進下，再加上無法證明以太的存在，愛因斯坦於1905年首次提出「光速不變」這一公設。[12][13]他從這一點推導出狹義相對論，並證明常數c在光和電磁波的範疇以外也有舉足輕重的地位。但是實驗只能驗證「雙向光速」（如：從光源至一面鏡子，再回到光源）是獨立於參考系的，但若要測量「單向光速」（如：從光源至某個遙遠的探測器），就必須先設定光源和探測器時鐘之間的同步化規則。如果選用愛因斯坦同步化規則，單向光速就會按照定義等同於雙向光速。[14][15]狹義相對論就是基於光速不變原理所得出的理論。它的另一個公設為：所有慣性參考系都擁有相同的物理定律。[16][17]其中一項結果，就是所有無質量粒子和相對應的波在真空中都以這一速度c運行和傳播，這也包括光波。

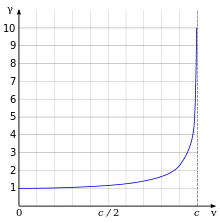
當v等於零時，γ等於1，然後γ隨著v的上升而上升，直至v趨近c時隨垂直漸近線趨向無限大。
勞侖茲因子γ作為速率v的函數。因子從1開始，並隨著v趨向c而趨向無限大。

狹義相對論有著不少有悖常理，卻有實驗證明的結果，[18]例如質能等價（E = mc2）、長度收縮（運動中的物體長度會縮小）[注 5]和時間膨脹（運動中的時鐘走得更慢）等。長度縮減及時間加長的比率γ稱為勞侖茲因子，其定義為γ = (1 − v2/c2)−1/2，其中v是物體的運動速度。在速度v比c小很多的情況下（包括大部份日常所見的慢速運動），γ很接近1。這時狹義相對論就可以近似為經典力學中的伽利略相對性。然而在v非常接近c時，γ趨向無限大，相對論性現象也就會呈現出來了。

要表述狹義相對論的各項結果，可以把時間和空間視為一種綜合的結構，即所謂的時空。狹義相對論還要求，所有物理理論均須遵守一種稱為勞侖茲協變性的特殊對稱性條件。無論是要結合時間和空間，還是要表達這種對稱性，在數學公式中都需要c這一常數。[21]勞侖茲協變性已幾乎成了現今物理理論的必需假設，這些現代理論包括量子電動力學、量子色動力學、粒子物理學標準模型及廣義相對論等。故此，c已成為現代物理學中無處不在的常數，出現在許多與光不相關的領域中。例如，廣義相對論預測，c也是引力波的傳播速度。[22][23]在非慣性參考系中（如受引力扭曲的時空和加速參考系等），「局部」光速是不變的並且等於c，但在有限長度內光的運行速度不一定等於c，且要視乎該參考系中距離和時間的具體定義。[24]

人們一般假設，諸如c等基礎常數在整個時空中都具有相同的數值，亦即它不會隨地點或時間而變動。（這種「不變性」不同於上文所述的各慣性參考系之間的光速不變性。）不過，有各種理論提倡，光速會隨時間改變。[25][26]目前尚未有確切證據證明光速可變，但對此的研究仍在繼續發展。[27][28]

人們同樣假設光速具有各向同性，也就是獨立於測量的方向。科學家在不同方向的磁場內對原子核的核能級發射光譜進行測量（對鐘實驗），又對旋轉光共振器進行觀測（見邁克生－莫立實驗），所得結果已對光速的各向異性設下了非常嚴格的上限。[29][30]

速度上限

根據狹義相對論，一個靜止質量為m、速度為v的物體含有能量γmc2，其中γ為上文定義的勞侖茲因子。當v為零的時候，γ等於1，這就得出廣為人知的質能等價公式E = mc2。當v接近c時，γ因子趨向無限大，所以需要無限大的能量才能把該物體加速到光速。光速也就是具有質量的物體的速度上限。這已經得到了眾多相對論能量動量實驗的證實。[31]

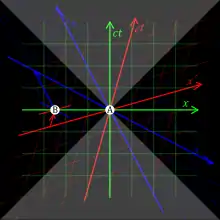
圖中共有三組座標，原點均位於A點。綠色座標中，橫軸為x，縱軸為ct；紅色座標中，x′軸稍稍向上偏斜，ct′軸則稍稍向右偏斜；藍色座標中，x′′軸稍稍向下偏斜，ct′′軸則稍稍向左偏斜。B點在綠色座標中位於A點的左邊，其ct值為零，ct′值大於零，且ct′′值小於零。
在紅色參考系中，事件A發生在事件B之前；在綠色參考系中，兩者同時發生；在藍色參考系中，A發生在B之後。

在正常情況下，訊息和能量的傳遞速度都不可能高於c。其中一個論證的方法來自於狹義相對論中「同時」的相對性。這一違反直覺的效應指出，如果事件甲和事件乙之間的距離大於兩者的時間間隔乘以c（即任何低於光速的訊息都無法把兩個事件聯繫起來），那麼就存在著甲乙發生先後次序不同的三個參考系：一個會測得甲發生在乙之前，一個測得兩者同時發生，一個則測得甲發生在乙之後。因此，一旦訊息在某個慣性參考系中的傳遞速度超過c，另一個參考系便會觀測到它倒著時間逆行，這將會違反因果關係。[注 6][33]在這樣的參考系裡，某「作用」會在其「起因」之前發生。如此的情況從未被觀察到，[15]若發生的話則會引致類似快子電話等的悖論。[34]

超光速觀測與實驗
条目：超光速
更多：超光速運動

有時候，物質、能量或訊息似乎會超光速運行，但這只是一種錯覺。例如，下文將會講述一些波在媒介中的速度可超過c。X射線的相速度在大部份玻璃中都高於c，[35]但這一速率並不是波傳遞訊息的速率。[36]

如果把激光束快速掃過一個遙遠的物體，這一光點的移動速度可以高於c。然而，真正在移動的物體只有激光器和它所發出的光子，而這些光子從激光器離開後，以光速射向遠處物體的各個部位。同樣，落在遙遠物體上的陰影也可以超光速移動。[37]在這些情況下，物質、能量和訊息都沒有超光速運行。[38]

如果有兩個物體都在相對某個參考系移動，它們之間距離的改變速率可以超過c。但在任何參考系中，單個物體的速度並沒有超過c。[38]

一些量子效應顯得可以超光速瞬時傳遞，如爱因斯坦-波多尔斯基-罗森佯谬。兩個粒子的量子態可以纏結起來。在任一個粒子被觀測之前，兩者的量子態都分別處於疊加的狀態。如果把兩個粒子分離開來，再對其中一個的量子態進行測量，就可立刻知道另一個粒子的量子態。有關第二個粒子量子態的訊息似乎以超過光速的速度抵達觀測者。不過，由於無法在一開始控制第一個粒子的量子態，所以還是沒有辦法利用這一現象來超光速傳遞訊息。[38][39]

哈特曼效應（）也是一種預測超光速運動的量子效應：在特定條件下，一個虛粒子進行量子穿隧的時間會獨立於障壁厚度。[40][41]這時，只要障壁的厚度足夠大，虛粒子就能超光速越過這一障礙。但同樣地，這一現象是無法用來傳遞訊息的。[42]

在天文觀測上，一些天體的視運動速度會超過光速，[43]如射電星系和類星體的相對論性噴流。不過，這類噴流的實際運動速度並沒有超過光速：當天體接近光速運行，且其運動方向與視線的夾角小的時候，就會在視覺上產生超光速運動的效果。噴流一開始所發出的光需時更久才到達地球，而稍後發出的光則需時較短。因此在地球觀測這兩束光的時間間隔比它們實際發出的時間間隔更短，噴流的速度也就顯得更高。[44]

在描述宇宙膨脹的模型中，星系之間的距離越大，相互遠離的速率亦越高。如果兩個星系相隔足夠遠，它們遠離對方的速度就可以超過光速。例如，星系退離地球的速度與它的距離成正比。在所謂的哈伯球邊緣以外，天體的退離速度會比光速更高。[45]但是，這種遠離的現象並不是因為天體在相對於空間運動，而是空間自身的膨脹所致。[38]

光的傳播

在古典物理學中，光是一種電磁波。電磁場的經典物理性質由麥克斯韋方程組所描述，其中電磁波在真空中就以速度c傳播。常數c與電常數ε0和磁常數μ0有以下的關係：c = 1/√ε0μ0。[46]在現代量子物理學中，電磁場由量子電動力學（QED）描述。QED理論中的光是電磁場中的最基本激發態（量子），又稱光子。光子不具質量，因此根據狹義相對論，它們在真空中必須以光速運行。

QED的一些延伸理論主張光子具有非零的質量。其運行速度取決於光的頻率，而狹義相對論的常數c就是光子在真空中運行的速度上限。[24]嚴謹的實驗從未探測出光的速度隨頻率的變化，[47][48][49]這為光子的質量設下了嚴格的質量上限。這一上限的具體數值要視乎所用的模型：若帶質量光子是由普洛卡理論（）描述的，[50]實驗所得的質量上限就是10−57克；[51]若用於描述的是希格斯機制，上限就會較為寬鬆：m ≤ 10−14 eV/c2[50]（約2 × 10−47 g）。

另一個提倡光速隨頻率改變的原因是，狹義相對論無法像某些量子引力理論推測的那樣，能應用到任意小的尺度上。2009年，科學家在測量了GRB 090510伽瑪射線暴的光譜之後，並沒有發現不同能量的光子有不同的速度。這意味著，勞侖茲不變性至少準確至普朗克長度（lP = √ħG/c3 ≈ 1.6163×10−35 米）除以1.2。[52]

参见：折射率

在媒介中，光的傳播速度一般都小于c，光在不同介质中会有不同的传播速度，这取决于該介質的折射率n（n = c / v）。例如，玻璃在可見光波段的折射率約為1.5，意味著光在玻璃中的速度為c / 1.5 ≈ 200000km/s；空氣在可見光波段的折射率約為1.0003，所以光在空氣中的速度約為299700km/s，比c慢90km/s。

不同類型的光波也會以不同的速度傳播。平面波（充斥整個空間，並只有一個頻率）的單個波峰和波谷的前進速度稱為相速度vp。實際的有限訊號（光脈衝）則會以不同的速度傳播。脈衝的最大部份以群速度vg前進，而脈衝的最前部份則以波前速度vf前進。

藍點隨著單個波峰和波谷移動（相速度），綠點隨波的包絡最大位置移動（群速度），紅點則隨脈衝的最前端移動（波前速度）
調製波從左至右移動。沿著波曲線移動的共有三點：藍點位於波的其中一個節點，綠點位於包絡的最大位置，紅點則位於包絡的最前端。

相速度會決定光如何穿過一個媒介，或如何從一個媒介跨越到另一個媒介中。這一速度通常以所謂的折射率來表示：一個媒介的折射率是c與相速度vp之比。折射率越高，相速度就越低。單一物質的折射率可受光的頻率、強度、偏振、傳播方向等的影響，不過通常可以假設折射率是一個只取決於物質屬性的常數。空氣的折射率約為1.0003。[53]密度更高的介質則具有更高的折射率：液態水、[54]玻璃和[55]鑽石[56]的折射率分別為1.3、1.5和2.4（可見光頻段）。在奇異材料中，例如接近絕對零度的玻色–愛因斯坦凝聚，光可以降速至每秒數米的速度。然而，光在媒介中的降速，純粹是因為光在原子間被吸收後再輻射的延時效果所造成的。以下是一個更極端的「光降速」的例子。美國麻省劍橋的兩個物理小組獨立研究，兩者都利用銣的玻色–愛因斯坦凝聚使光在其中「完全停止」。不過，在這一現象中，光只是被暫時儲存在原子的激發態中，在另一激光脈衝的激發下，隨時可重新發射出來。在被停頓的那一段時間內，原來的光並不處於光的狀態。所有透明材料使光降速的現象，在微觀尺度下的原理都和以上的例子相似。[57]

透明材料的折射率一般高於1，代表相速度低於c。但某些頻率的光在某些材料中的折射率可以低於1，有時甚至可低於零（負折射率）。[58]然而正如上文所述，因果關係是不可違反的，所以任何物質的介電常數的實部和虛部──分別對應於折射率和衰減係數──必須遵守克拉莫-克若尼關係式。[59]簡單地來說，如果材料的折射率低於1，波就會在其中被迅速吸收，使得訊息不可能以超過c的速度傳遞。

如果組成脈衝的各個頻率有不同的相速度，那麼脈衝的相速度和群速度就會不同，而且會隨時間攤開變平，這一現象稱為色散。一些材料的光波群速度特別低（甚至等於零），這種情況稱為慢光。許多實驗都能夠證實這種現象的發生。[60][61][62][63]另一方面，也有實驗證明相反現象的存在：群速度超過c。[64]理論上，群速度甚至有可能無限大，即脈衝瞬時傳播；或是負數，即脈衝隨時間反向行進。[65]


粒子在介質中的運動速度可以超過光在其中的相速度（但仍低於c）。當帶電粒子在介電質中的運動速度超過光的相速度，它就會發射出類似激波的切倫科夫輻射。[66]

光速有限在應用上的影響

光速有限在通訊方面有重要的意義：單向及來回通訊延遲時間不為零。它的影響範圍小至電子學，大至天文學。另一方面，光速不變的性質可以用來測量距離。

小尺度

光速為超級電腦中處理器之間數據傳輸的速度設下限制。如果處理器的時脈為1GHz，那麼在一個時鐘週期內，訊號的傳送距離就只有大約30cm。必須縮減處理器之間的距離，才可避免通訊延遲，但這又會使冷卻更為困難。不斷提升的時脈最終甚至會限制單個晶片的內部設計。[67]

地球上的通訊

地球赤道周長為40075 km，而c大約等於300000000 m/s，所以資訊沿著地球表面需時67毫秒才能行進半個地球的距離。光在光纖中的實際傳遞時間則會更長，因為光纖內的光速比c慢大約35%，具體數值同折射率n相關。[68]更甚者，全球性通訊很少用到兩點之間的最短距離，而且訊號在通過電開關和訊號再生器時還會加入額外的延時。[69]

航天與天文學
動畫中，月球的直徑約為地球的四分之一，兩者相距約30個地球直徑。從地球離開的光束到達月球需時約1.3秒。
動畫顯示一束光離開地球，以有限的速度射向月球。假設地月平均距離，光束從地球表面到月球表面需時1.255秒。圖中地月系統的相對大小和距離均依照實際比例繪出。

地球與航天器之間的通訊無法瞬時傳遞。有限光速所帶來的訊號延時會隨著距離的增大而變得更明顯。當阿波羅8號成為首艘進入月球軌道的載人飛船時，它與地面任務控制中心的通訊就有明顯的延時：從地面發出的提問至少要等3秒才會得到回覆。[70]地球和火星之間的通訊延時介乎5到20分鐘，具體數字要看當時兩者的相對位置。若位於火星表面的機械人遇到問題，地面的控制人員要等5到20分鐘才會收到消息，接著發出的指令又要等待5到20分鐘才會抵達火星。地面與木星探測器的通訊延時高達數小時。一旦發生導航錯誤並須要人為干預，會有錯過時機的危險。

來自其他遙遠天體的光和訊號需要長得多的時間才能到達地球。例如，哈勃超深空影像中來自極遠星系的光，在被探測之前已經過了130億（13×109）年的飛行時間。[71][72]這些圖片所捕捉到的，是這些星系130億年前的樣子，當時的宇宙年齡還不到10億年。[71]有限的光速使得天文學家能夠觀察遠處天體更年輕時的樣貌，從而研究恒星、星系和宇宙的演化。

天文距離有時會以光年作單位，特別是在科普作品和媒體報導之中。[73]一光年等於光在一年的時間內所行進的距離，約等於9.461兆（萬億）公里，又等於0.3066秒差距。比鄰星是除太陽以外最接近地球的恒星，其距離地球約4.2光年。[74]

距離測量

雷達系統通過發出無線電波，並測量電波從目標反射回來後的總時間，從而計算目標的距離。目標的距離是來回飛行時間的一半，乘以光速。全球定位系統（）接收器通過測量來自各個衛星的電波訊號的抵達時間，計算它與這些衛星的距離，再推算接收器在地球上的位置。由於光在一秒內能行進30萬公里，所以這些時間的測量必須非常精准。月球激光測距實驗、射電天文學和深空網絡利用來回飛行時間，分別量度月球、[75]各大行星[76]及航天器[77]的距離。

高頻交易

光速在高頻交易當中有重要的意義。交易者為了在進行交易時快人一步，已開始在在各交易中心之間使用微波通訊，因為光纖內的光速比c慢30%至40%，而微波在大氣層中的速度則非常接近c。[78]

測定

奧勒·羅默於1676年首次測定光速。他通過研究木衛一的視運動，判斷出光的傳播速度是有限的，而非無限。 光速c的測量方法有若干種。最直接的方法是量度光波行進的實際速度，不同的天文和地面設備都可以這樣測定光速。不過，還可以通過測量其他物理常數，再利用物理定律來推算出c，例如用ε0和μ0與c的關係。在歷史上，最準確的光速測量方法是分別量度光束的頻率和波長，兩者相乘後得出c。

在一般情況下，光以及其他電磁波都似乎能夠從甲點瞬間達到乙點，但只要甲乙兩點相隔距離大，再加上精度極高的測量儀器，就可测得到光的傳播速度所呈現的各種現象。在与遙遠的空間探測器通訊的時候，從地球發出的訊號需數分鐘甚至數小時的時間才可抵達探測器，反之亦然。同樣，來自遙遠星體的光經過許多年才到達地球，因此科學家可通過觀測這些星體來研究宇宙久遠的歷史。光速還可以用在所謂的「飛行時間」測量法中，以高精確度量度兩個相距較遠的點之間的距離。

1983年，國際單位制將米重新定義為「1⁄299792458秒內光在真空中行進的距離」，[79]從此把光速的準確數值設為299792458 m/s（詳見下文）。因此，更準確地測量光速將不再提高c數值的精度，而是會使「一米」的定義更加準確。

天文測量法
通過觀察木星掩食木衛一的時間來判斷光速

外太空是測定光速的理想場地，因為它空間大，又處於近乎真空的狀態。一般人們會量度光走過太陽系內某個基準距離所需的時間，例如地球軌道半徑。過去人們用這種方法測量的光速數值可以較為準確地表達成常用單位，但實際準確度要視乎基準距離的準確度。這樣得出的光速通常以天文單位（）每天的單位表示。

奧勒·羅默於1676年用天文方法首次對光速進行測定。[80][81]從地球觀測，衛星圍繞行星公轉的週期在地球向其靠近時會縮短，在地球遠離它的時候則會加長。光從彼方到達地球所需的時間，在地球距離該行星（及其衛星）最近時，比兩者相距最遠時更短，此二距離只差就是地球繞日軌道的直徑。光運行時間的差異，就會導致衛星公轉週期在觀測上的差異。羅默在木星和木衛一系統中觀察到這種現象，並依此推斷光橫跨地球軌道直徑需要22分鐘的時間。

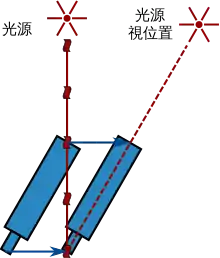
一顆恒星發出的光束落在望遠鏡的物鏡上。光在望遠鏡內向目鏡行進的同時，望遠鏡向右移動。要使光束沿著望遠鏡內部行進，望遠鏡就要向右傾斜，使光源的影像位於實際位置的右邊。
光行差：由於光速有限，來自遠處的光會因望遠鏡的移動而產生視覺上位移。

另一個方法是測量光行差。詹姆斯·布拉德雷於18世紀發現並描述這一現象。[82]光行差現象是來自遙遠光源的光束速度與觀測者速度的向量和所致。對於移動中的觀測者來說，光源的位置會偏離其實際位置。由於地球繞日公轉的速度是連續變化的，所以光行差會使恒星的視位置來回移動。根據恒星在天球上位置的最大角度差（最多達20.5弧秒），[83]可以推算出光速和地球公轉速率之間的關係。利用一年的已知時長，就可以換算出光從太陽抵達地球所需時間。1729年，布拉德雷用光行差算出，光速比地球公轉速率快10,210倍（實際為10,066倍）。[82]

天文單位

一個天文單位（）約等於地日平均距離。2012年，國際單位制將天文單位定義為準確值149597870700 米。[84][85]此前，天文單位的定位基礎並不是國際單位制，而是在經典力學框架下以太陽所施的引力來表示。[注 7]目前的定義則用到舊定義時所測量出、以米作為單位的數值。[84]對天文單位的重新定義，和對米的重新定義有相同的意義：從此光速就有了「天文單位每秒」的準確數值（從「米每秒」的準確數值換算出）。

在重新定義之前，c的倒數，即「秒每天文單位」，可以通過對比無線電訊號抵達太陽系各處航天器所需的時間推算而得。用多個數據點繪圖，便可得出光運行單位長度所需時間的最佳擬合數值。在2009年，經國際天文聯會認可的最佳估值為：[87][88]

光運行單位長度需時：499.004783836(10) s
c = 0.00200398880410(4) AU/秒 = 173.144632674(3) AU/天。

以上數值的相對不確定性為10億分之0.02（2×10−11），相等於在地球表面使用干涉測量術測量距離的不確定性。[89]由於米已被定義為光在特定時間內行進的距離，所以在舊定義下以天文單位來表達光速，相當於以米單位來測量天文單位（舊定義）的長度。[注 8]

飛行時間法
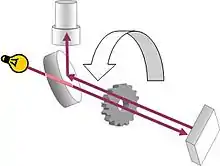
光束橫向穿過半透鏡和旋轉嵌齒輪，由鏡子反射，再穿過嵌齒輪，最後由半透鏡反射到單筒鏡中。
斐索-傅科儀示意圖

另一種測定光速的方法是在已知距離外放下一面鏡子，再量度光到達鏡子反射回來的時間。這是阿曼德·斐索和萊昂·傅科發明的斐索-傅科儀的原理。

斐索把一束光射向8公里以外的一面鏡子。在光束的路徑上有一個旋轉的嵌齒輪。在特定的轉速下，光束出去時穿過齒輪的縫隙，回來時又會穿過另一個縫隙。但一旦轉速稍微不同，回來的光束就會被輪齒擋住，不能通過。只要知道嵌齒輪和鏡子間的距離、輪齒數目及轉速，就可計算出光速。[90]

傅科的做法則是用旋轉的鏡子代替嵌齒輪。由於光在兩個方向運行的時候中間的鏡子會繼續旋轉，所以光在出去時和回來時會以不同的角度被中間的鏡子反射。只要知道角度之差、鏡子的轉速和遠處鏡子的距離，就可算出光速。[91]

今天，利用時間分辨率小於1納秒的示波器，可以直接量度激光或LED光從鏡子反射回來的延時。這種方法的精確度比其他現代測量法低（誤差在1%的數量級），但有時會在大學物理課上作演示之用。[92][93][94]

電磁常數

麥克斯韋電磁理論將c與真空電容率ε0和真空磁導率μ0聯繫起來：c2 = 1/(ε0μ0)。真空電容率可以通過測量已知大小電容器的電容所得；由於安培單位的定義，真空磁導率的準確值被固定在4π×10−7 H*m-1。Rosa和Dorsey在1907年用這種方法得出的光速值為299710±22 km/s。[95][96]

諧振腔
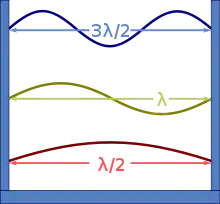
一個盒子內有三個波，最上方的在盒內共有一個半波長，中間的有一個波長，最下方的有半個波長。
空腔內的電磁駐波

光速還可以通過分別測量光在真空中的頻率f和波長λ而得。兩者相乘後就可得出c的數值：c = fλ。其中一種方法是測量空腔諧振器的頻率。如果同時亦知道諧振腔的尺寸，就可以算出波長。1946年，路易斯·艾森（）和A·C·戈登-史密斯（）測量了各種微波正交模在已知尺寸的微波諧振腔內的頻率。他們所用的標準尺寸是用干涉法校準的，所量得的諧振腔尺寸準確至約±0.8 μm。[95]運用電磁學理論，可以從諧振腔的形狀推算出模態的波長。這就足以算出光速的數值了。[95][97]

艾森和戈登-史密斯所取得的數值299792±9 km/s比此前用光學方法取得的要準確得多。[95]艾森重複進行測量，到了1950年得出的數值為299792.5±3.0 km/s。[98]

這種方法可以用家居微波爐和棉花糖或牛油等食物來示範。如果把轉盤拿走，食物就不會在爐內轉動。這時食物在反節點（波幅最高處）的煮熟時間最短，這可以通過觀察它的融化過程來判斷。兩個反節點之間的距離等於波長的一半。若將波長乘以微波的頻率（一般在微波爐背部標示，通常是2450 MHz），就可算出光速，誤差可以在5%以下。[99][100]

干涉法
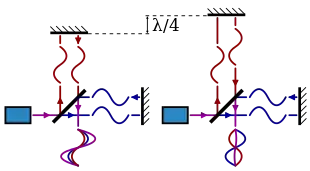
邁克生干涉儀原理示意圖
干涉測量法的原理。左：相長干涉；右：相消干涉

干涉測量法也是一種量度光波波長的方法。[101]一束已知頻率（f）的相干光（如激光）在被分開行走不同路徑後重新結合起來。在調整路徑長度的同時觀察干涉圖樣，又對路徑長度作非常準確的測量，就可以得出波長（λ）。計算光速的公式同上：c = λf。

在激光科技的發明之前，科學家曾使用無線電波進行干涉法來測定光速。[102]然而，波長越長，干涉法所得出的波長數值就越不準確，因此較早取得的數值準確度受到了無線電波長（約0.4 cm）的限制。通過降低電磁波的波長，可以增加準確度，但就增加了直接測量頻率的難度。一個解決方法是，先從頻率能夠準確測得的低頻訊號開始，再在低頻訊號的基礎上建立更高頻訊號。這時可以把激光鎖定到這一頻率，激光的波長就可以用干涉儀得出了。[103]此方法是美國國家標準局（今國家標準技術研究所）的一個小組所發明的。他們在1972年測量光速的不確定性分數為3.5×10−9。[103][104]

歷史
光速測量年表
年份測定者方法數值（km/s） 相對於1983年標準值誤差
1675羅默和惠更斯木星衛星220000[81][105] -26.6%
1729詹姆斯·布拉德雷光行差301000[90] +0.403%
1849阿曼德·斐索旋轉嵌齒輪315000[90] +5.07%
1862萊昂·傅科旋轉鏡子298000±500[90] -0.598%
1907Rosa和Dorsey電磁常數299710±30[95][96] -0.0275%
1926阿爾伯特·邁克生旋轉鏡子299796±4[106] +0.00118%
1950艾森和戈登-史密斯諧振腔299792.5±3.0[98] +0.0000140%
1958K.D. Froome無線電干涉法299792.50±0.10[102] +0.0000140%
1972Evenson等人激光干涉法299792.4562±0.0011[104] -0.00000000601%
1983第17屆國際度量衡大會對米重新定義299792.458（準確值）[79]

直到近代以前，人們都不知道光是瞬間傳遞，還是以極快的有限速度傳遞。對這一問題有記載的最早研究是在古希臘時期。古希臘、伊斯蘭世界以及歐洲古典學者都對此進行了長期的討論，直到羅默首次測出光速，並得出了結論。到了20世紀，愛因斯坦的狹義相對論指出，光的速度無論在任何參考系中都是一樣的。自此，科學家對光速的測量數值越來越準確，直到1983年國際單位制對米的重新定義把光速固定為一個準確值。

早期歷史

恩培多克勒（前490－前430年）是歷史記載中第一個宣稱光速有限的人。[107]他相信光是一種運動的東西，所以運行需要時間。亞里士多德卻認為，「光是因某物存在所致，而不是一種運動的東西」。[108]歐幾里得和托勒密繼續發展了恩培多克勒的「發射理論」，即視覺是眼睛發射光線所產生的。根據這一理論，亞歷山大港的希羅推論光速一定是無限的，因為睜開眼睛的那一剎那就可以看到遙遠的物體。

早期伊斯蘭哲學思想和亞里士多德理論一樣相信光速無限。1021年，海什木的著作《光學》闡述了一連串推翻發射理論、支持「進入理論」的論據，也就是主張來自物體的光線進入眼睛，產生視覺。[109]海什木因此提出光必定以有限的速度傳播，[108][110][111]而且光速是可變的──它在密度高的物質內的速度較慢。[111][112]他又推論，光是一種物質，傳遞是需要時間的，儘管我們在感官上無法觀察得到。[113]同樣在11世紀的阿布·拉伊汗·穆罕默德·本·艾哈邁德·比魯尼也認為光速有限，而且觀察到光速比音速快得多。[114]

13世紀的英國科學家羅吉爾·培根在海什木和亞里士多德著作的基礎上論述，光在空氣中的速度不是無限的。[115][116]1270年代，波蘭科學家威特羅（）認為，光有可能在真空中以無限的速度傳遞，要在具有密度的物體中才會降速。[117]

17世紀初，德國科學家約翰內斯·開普勒相信光速是無限的，因為一無所有的空間裡沒有任何阻礙光線前進的東西。勒內·笛卡兒則論述，如果光速是有限的，太陽、地球和月球在月食之時就會有明顯的錯位。由於人們從沒有觀察到這樣的錯位現象，所以光速是無限的。他甚至認為，如果發現光速是有限的話，他的整套哲學系統可能會因此崩潰。[108]儘管光速是無限的，笛卡兒在對斯涅爾定律的推導當中仍然假設，材料密度較高，其中的光速就越高。[118]皮埃爾·德·費馬則支持光速有限的說法，並且在推導斯涅爾定律時用到與笛卡兒相反的假設：介質密度越高，光線的速度就越低。[119]

最早的測定

1629年，荷蘭科學家以撒·貝克曼（）提出用肉眼觀測大炮的閃光在大約一英里（1.6公里）外一面鏡子反射回來，從而計算光速。1638年，意大利科學家伽利略·伽利萊提出一項他聲稱曾經做過的實驗，當中的一方遮掩一盞燈，另一方在一段距離外觀察這一動作的延時，再立即遮掩另一盞燈示意。他無法以此辨別光速是有限還是無限的，但他得出的結論是，就算光速是有限的，它也肯定快到不可思議的程度。[120][121]意大利佛羅倫斯的實驗學會（）於1667年進行了伽利略的實驗。在兩盞燈相距約一英里的情況下，沒有觀察到任何的延時。用今天的已知光速計算，當時的延時只有11微秒。

木衛一掩食示意圖：地球和木星繞太陽公轉，木衛一則繞木星公轉。圖中繪出木星的陰影。
羅默從地球觀測木衛一被木星掩食

奧勒·羅默於1676年首次對光速進行測定。[80][81]他觀察到，木衛一繞木星的公轉週期在地球靠近木星的時候，比地球遠離木星時更短。他從這一點推論光速一定以有限的速度傳播，並估算光橫跨地球的公轉軌道直徑需時22分鐘。克里斯蒂安·惠更斯利用這一數據，加上對地球軌道直徑的估值，計算出光速大約為220000 km/s，比實際數值低了26%。[105]

艾薩克·牛頓在1704年著作《光學》中描述了羅默對光速的計算，並算出光從太陽到達地球需時「七至八分鐘」（實際數值為8分鐘19秒）。[122]牛頓問道羅默所觀察到的掩食陰影有沒有顏色，並在得知否定的答案後，得出「不同顏色的光之速度相同」的結論。1729年，詹姆斯·布拉德雷發現恒星光行差的現象。[82]他以此算出，光速比地球公轉速度快10,210倍（實際數值為10,066倍），相等於光從太陽到達地球需時8分鐘12秒。[82]

與電磁學的關係
参见：狭义相对论发现史

德國數學家黎曼於1858年提交給哥廷根科學學會的論文中，提出光的電磁理論：

阿曼德·斐索在19世紀發明了在地球上進行的「飛行時間測量法」，並得出315000 km/s的光速數值。萊昂·傅科進一步完善了斐索的方法，在1862年所得出的數值為298000 km/s。[90]1856年，威廉·愛德華·韋伯和魯道夫·科爾勞施通過萊頓瓶的放電測量出電磁單位荷和靜電單位荷之比（1/√ε0μ0），並發現這與斐索此前所測得的光速非常接近。翌年，古斯塔夫·基爾霍夫算出電訊號在無電阻導體中的傳遞速度也等於此數值。[125]1860年代初，麥克斯韋在發展電磁理論的時候證明，電磁波在真空中的傳播速度[126][127][128]相等於韋伯和科爾勞施得出的比值。由於比值和斐索的光速非常相近，麥克斯韋因此提出，光其實是一種電磁波。[129]

以太
亨德里克·勞侖茲（右）和阿爾伯特·愛因斯坦（左）合照

20世紀以前的物理學家曾以為空間充斥著一種稱為「以太」的介質，電磁波就在其中傳播。一些物理學家把以太視為「絕對靜止」的參考系，所以理論上可以通過記錄光速的變化來測量地球相對於以太的運動。從1880年代起曾進行了不少旨在探測這種運動的實驗，其中最廣為人知的要數1887年的邁克生－莫立實驗了。[130]結果顯示，相對以太的運動總是比觀測不確定性小。更近期的實驗指出，雙向光速的各向異性（即隨觀測方向而變化）不大於6納米每秒。[131]亨德里克·勞侖茲根據這一點，提出儀器在以太中的運動會導致它的自身長度沿著運動方向的收縮，而且移動系統所測量的時間也會隨之改變（「局部時間」），這就發展出勞侖茲變換。在勞侖茲以太理論的基礎上，昂利·龐加萊於1900年證明，這一局部時間（一階近似）可以由相對以太移動中的時鐘表示，而時鐘是在光速不變的假設下同步化的。1904年，他猜測一旦勞侖茲的理論得到證實，光速就有可能是力學上的速度極限。1905年，龐加萊證明勞侖茲以太理論在觀測上和相對性原理完全相符。[132][133]

狹義相對論

1905年，阿爾伯特·愛因斯坦設想，非加速觀測者所測得的光速獨立於光源及觀測者自身的運動。以此作為公設，他繼而建立起整套狹義相對論。理論中，真空中的光速c是一個基礎常數，出現的地方也不僅限於光的傳播。物理定律不再需要一個絕對靜止的參考系，因此這一舉動完全淘汰了當時勞侖茲和龐加萊仍然堅持的以太理論，也大大革新了人們對空間和時間的觀念。[134][135]


光速精確度的提升與米和秒的重新定義

20世紀下半葉，光速的測量準確度隨著諧振腔和激光干涉儀的發展而不斷地提升。另一方面，更精確的米和秒的定義也陸續被認可。1950年，路易斯·艾森用諧振腔所得出的光速值為299792.5±1 km/s。這在1957年的第12屆無線電學聯合會大會上得到採納。1960年，米被重新定義，基礎是氪-86的某個譜線的波長。1967年，秒也被重新定義，基礎是銫-133基態的超精細躍遷頻率。

1972年，位於美國科羅拉多州波德的國家標準技術研究所利用激光干涉法測定光速，得出c = 299792456.2±1.1 m/s，其精度比之前的測量高100倍。剩餘的不確定性主要來自米定義上的不確定性。[注 9][104]由於類似的實驗也得出相近的光速值，所以1975年的第15屆國際度量衡大會建議把299792458 m/s作為光速的數值。[138]

明確固定光速的數值

1983年的第17屆國際度量衡大會結果發現，通過測量頻率並固定某一特定光速值所得出的波長比此前的長度單位定義更具有可重複性。大會保留了1967年的秒定義，使銫的超精細頻率成為秒和米兩個單位的定義基礎。米的定義改為：「1⁄299792458秒內光在真空中所運行的距離。」[79]在這一定義下，光速的準確值就會固定在299792458 m/s，[139][140]光速也成了國際單位制所定義的常數之一。[8]在重新定義之前，更準確的測量會使光速值變得更為精確；但在1983年以後，對氪-86以及其他光源的更準確測量不會再改變現有的光速值，而是會增加米單位的精確度。[141][142]

度量衡大會在2011年表示，整個國際單位制中的七個基本單位都會通過所謂的「明確常數制定方法」來重新定義：「每一個單位都會以明確固定某個廣泛認可的基礎常數來間接地定義」，也就是米的定義與光速之間的關係。在該提議下，米有了本質完全相同但措辭不同的定義：「米，符號m，是長度的單位；定義為光速在SI單位m s−1下的數值固定為299792458後，所設定的值。」[143]這將成為國際單位制的新修訂內容之一。

参見

備註
  1. 精確值：
    (299792458×3600/1000)
  2. 精確值：
    (299792458×60×60×24/149597870700) AU/天
  3. 在英制單位和美制單位中，一英寸的定義為2.54 cm，所以光速的精確值為186,282英里698碼2呎5+21/127吋每秒。[9]
  4. 不過，光的頻率卻取決於波源和觀測者之間的相對運動，即所謂的多普勒效應。
  5. 運動物體的長度在測量上會變短，但同時在視覺觀測上還會有額外的旋轉。這一效應是光從物體的各部位到達觀測者需時差異所致，稱為特雷爾轉動。[19][20]
  6. 沙恩霍斯特效應（）可能能夠使訊號傳播的速度稍超過c，但該效應所需的特殊條件會防止因果關係被違反。[32]
  7. 天文單位的舊定義為：一個無限小質量以每天0.01720209895弧度（約佔公轉一週的1⁄365.256898）的角頻率圍繞太陽作無攝動牛頓圓軌道公轉時的軌道半徑。[86]
  8. 當然，在精度如此高的情況下，必須考慮到廣義相對論的效應。米是量度原長的單位，而天文單位卻通常是量度給定座標系所觀測到的長度。以上給出的數值符合後者，且與質心力學時間（）相容。[88]
  9. 在1960年和1983年間，米的定義為：「氪-86原子中2p10和5d5能級之間躍遷所發出的輻射在真空中的波長乘以1650763.73。」[136]到了1970年代，人們發現該譜線並不是對稱的。因此在這一定義下，干涉法對米單位的測定就有了精確度上的極限。[137]

參考資料
  1. Penrose, R. . Vintage Books. 2004: 410–1. ISBN 978-0-679-77631-4. ... the most accurate standard for the metre is conveniently defined so that there are exactly 299,792,458 of them to the distance travelled by light in a standard second, giving a value for the metre that very accurately matches the now inadequately precise standard metre rule in Paris.
  2. Gibbs, P. . Usenet Physics FAQ. University of California, Riverside. 2004 [1997] [2009-11-16]. （原始内容存档于2009-11-17）.
  3. Mendelson, KS. . American Journal of Physics. 2006, 74 (11): 995–997. Bibcode:2006AmJPh..74..995M. doi:10.1119/1.2238887.
  4. 請見：
    • Lide, DR. . CRC Press. 2004: 2–9. ISBN 0-8493-0485-7.
    • Harris, JW; et al. . Springer. 2002: 499. ISBN 0-387-95269-1.
    • Whitaker, JC. . CRC Press. 2005: 235. ISBN 0-8493-1889-0.
    • Cohen, ER; et al. 3rd. Royal Society of Chemistry. 2007: 184. ISBN 0-85404-433-7.
  5. International Bureau of Weights and Measures, (PDF) 8th: 112, 2006, ISBN 92-822-2213-6 （英语）
  6. Sydenham, PH. . Boyes, W (编). 3rd. Butterworth–Heinemann. 2003: 56 [2015-05-23]. ISBN 0-7506-7123-8. （原始内容存档于2014-09-21）. ... if the speed of light is defined as a fixed number then, in principle, the time standard will serve as the length standard ...
  7. . The NIST reference on Constants, Units, and Uncertainty. NIST. [2009-08-21]. （原始内容存档于2017-06-25）.
  8. Jespersen, J; Fitz-Randolph, J; Robb, J. Reprint of National Bureau of Standards 1977, 2nd. Courier Dover. 1999: 280. ISBN 0-486-40913-9.
  9. Savard, J. . John Savard's Home Page. [2009-11-14]. （原始内容存档于2009-11-14）.
  10. Lawrie, ID. . 2nd. CRC Press. 2002: 540 [2015-05-23]. ISBN 0-7503-0604-1. （原始内容存档于2014-09-21）.
  11. Hsu, L. . 2nd. World Scientific. 2006: 427–8 [2015-05-23]. ISBN 981-256-651-1. （原始内容存档于2014-09-21）.
  12. Stachel, JJ. . Springer. 2002: 226 [2012-08-06]. ISBN 0-8176-4143-2. （原始内容存档于2013-06-23）.
  13. Einstein, A. . Annalen der Physik. 1905, 17: 890–921. Bibcode:1905AnP...322..891E. doi:10.1002/andp.19053221004 （德语）.英文翻譯：Perrett, W; Jeffery, GB (tr.); Walker, J (ed.). . Fourmilab. [2009-11-27]. （原始内容存档于2011-04-25）.
  14. Hsu, J-P; Zhang, YZ. . Advanced Series on Theoretical Physical Science 8. World Scientific. 2001: 543ff. ISBN 981-02-4721-4.
  15. Zhang, YZ. . Advanced Series on Theoretical Physical Science 4. World Scientific. 1997: 172–3 [2015-05-23]. ISBN 981-02-2749-3. （原始内容存档于2012-05-19）.
  16. d'Inverno, R. . Oxford University Press. 1992: 19–20. ISBN 0-19-859686-3.
  17. Sriranjan, B. . . PHI Learning Pvt. Ltd. 2004: 20 ff [2015-05-23]. ISBN 81-203-1963-X. （原始内容存档于2015-03-20）.
  18. Roberts, T; Schleif, S; Dlugosz, JM (ed.). . Usenet Physics FAQ. University of California, Riverside. 2007 [2009-11-27]. （原始内容存档于2009-10-15）.
  19. Terrell, J. . Physical Review. 1959, 116 (4): 1041–5. Bibcode:1959PhRv..116.1041T. doi:10.1103/PhysRev.116.1041.
  20. Penrose, R. . Proceedings of the Cambridge Philosophical Society. 1959, 55 (01): 137–9. Bibcode:1959PCPS...55..137P. doi:10.1017/S0305004100033776.
  21. Hartle, JB. . Addison-Wesley. 2003: 52–9. ISBN 981-02-2749-3.
  22. Hartle, JB. . Addison-Wesley. 2003: 332. ISBN 981-02-2749-3.
  23. 一些科學家對通過觀測雙星系統來推算出引力的傳播速度持懷疑的態度，所以這一點在實驗驗證上仍無定論。見：Schäfer, G; Brügmann, MH. . Dittus, H; Lämmerzahl, C; Turyshev, SG (编). . Springer. 2008. ISBN 3-540-34376-8.
  24. Gibbs, P. Carlip, S , 编. . Usenet Physics FAQ. University of California, Riverside. 1997 [1996] [2009-11-26]. （原始内容存档于2009-11-17）.
  25. Ellis, GFR; Uzan, J-P. . American Journal of Physics. 2005, 73 (3): 240–7. Bibcode:2005AmJPh..73..240E. arXiv:gr-qc/0305099 可免费查阅. doi:10.1119/1.1819929. The possibility that the fundamental constants may vary during the evolution of the universe offers an exceptional window onto higher dimensional theories and is probably linked with the nature of the dark energy that makes the universe accelerate today.
  26. 請見以下論文中的概述：Mota, DF. . 2006. arXiv:astro-ph/0401631 可免费查阅 |class=被忽略 (帮助).
  27. Uzan, J-P. . Reviews of Modern Physics. 2003, 75 (2): 403. Bibcode:2003RvMP...75..403U. arXiv:hep-ph/0205340 可免费查阅. doi:10.1103/RevModPhys.75.403.
  28. Amelino-Camelia, G. . 2008. arXiv:0806.0339 可免费查阅 [gr-qc].
  29. Herrmann, S; et al. . Physical Review D. 2009, 80 (100): 105011. Bibcode:2009PhRvD..80j5011H. arXiv:1002.1284 可免费查阅. doi:10.1103/PhysRevD.80.105011.
  30. Lang, KR. 3rd. Birkhäuser. 1999: 152. ISBN 3-540-29692-1.
  31. Fowler, M. (PDF). University of Virginia: 56. March 2008 [2010-05-07]. （原始内容存档 (PDF)于2013-02-01）.
  32. Liberati, S; Sonego, S; Visser, M. . Annals of Physics. 2002, 298 (1): 167–85. Bibcode:2002AnPhy.298..167L. arXiv:gr-qc/0107091 可免费查阅. doi:10.1006/aphy.2002.6233.
  33. Taylor, EF; Wheeler, JA. . W. H. Freeman. 1992: 74–5. ISBN 0-7167-2327-1.
  34. Tolman, RC. . Reprint. BiblioLife. 2009: 54 [1917]. ISBN 978-1-103-17233-7.
  35. Hecht, E. 2nd. Addison-Wesley. 1987: 62. ISBN 0-201-11609-X.
  36. Quimby, RS. . John Wiley and Sons. 2006: 9 [2015-05-23]. ISBN 978-0-471-71974-8. （原始内容存档于2014-09-21）.
  37. Wertheim, M. . The New York Times. 2007-06-20 [2009-08-21]. （原始内容存档于2013-05-10）.
  38. Gibbs, P. . Usenet Physics FAQ. University of California, Riverside. 1997 [2008-08-20]. （原始内容存档于2009-11-17）.
  39. Sakurai, JJ. T, S , 编. Revised. Addison-Wesley. 1994: 231–232. ISBN 0-201-53929-2.
  40. Muga, JG; Mayato, RS; Egusquiza, IL, eds. . Springer. 2007: 48. ISBN 3-540-73472-4.
  41. Hernández-Figueroa, HE; Zamboni-Rached, M; Recami, E. . Wiley Interscience. 2007: 26. ISBN 0-470-10885-1.
  42. Wynne, K. (PDF). Optics Communications. 2002, 209 (1–3): 84–100. Bibcode:2002OptCo.209...85W. doi:10.1016/S0030-4018(02)01638-3. archive
  43. Rees, M. . Nature. 1966, 211 (5048): 468. Bibcode:1966Natur.211..468R. doi:10.1038/211468a0.
  44. Chase, IP. . Usenet Physics FAQ. University of California, Riverside. [2009-11-26]. （原始内容存档于2010-04-16）.
  45. Harrison, ER. . Cambridge University Press. 2003: 206. ISBN 0-521-77351-2.
  46. Panofsky, WKH; Phillips, M. . Addison-Wesley. 1962: 182. ISBN 978-0-201-05702-7.
  47. Schaefer, BE. . Physical Review Letters. 1999, 82 (25): 4964–6. Bibcode:1999PhRvL..82.4964S. arXiv:astro-ph/9810479 可免费查阅. doi:10.1103/PhysRevLett.82.4964.
  48. Ellis, J; Mavromatos, NE; Nanopoulos, DV; Sakharov, AS. . Astronomy & Astrophysics. 2003, 402 (2): 409–24. Bibcode:2003A&A...402..409E. arXiv:astro-ph/0210124 可免费查阅. doi:10.1051/0004-6361:20030263.
  49. Füllekrug, M. . Physical Review Letters. 2004, 93 (4): 043901. Bibcode:2004PhRvL..93d3901F. doi:10.1103/PhysRevLett.93.043901.
  50. Adelberger, E; Dvali, G; Gruzinov, A. . Physical Review Letters. 2007, 98 (1): 010402. Bibcode:2007PhRvL..98a0402A. PMID 17358459. arXiv:hep-ph/0306245 可免费查阅. doi:10.1103/PhysRevLett.98.010402.
  51. Sidharth, BG. . World Scientific. 2008: 134. ISBN 981-281-234-2.
  52. Amelino-Camelia, G. . Nature. 2009, 462 (7271): 291–292. Bibcode:2009Natur.462..291A. PMID 19924200. doi:10.1038/462291a. （原始内容存档于2015-03-26） 使用|archiveurl=需要含有|url= (帮助). 简明摘要 – Nature (19 November 2009).
  53. de Podesta, M. . CRC Press. 2002: 131. ISBN 0-415-25788-3.
  54. . refractiveindex.info. Mikhail Polyanskiy. [2010-03-14]. （原始内容存档于2010-03-25）.
  55. . refractiveindex.info. Mikhail Polyanskiy. [2010-03-14]. （原始内容存档于2010-04-12）.
  56. . refractiveindex.info. Mikhail Polyanskiy. [2010-03-14]. （原始内容存档于2010-05-03）.
  57. Harvard News Office. . News.harvard.edu. 2001-01-24 [2011-11-08]. （原始内容存档于2011-10-28）.
  58. Milonni, PW. . CRC Press. 2004: 25. ISBN 0-7503-0926-1.
  59. Toll, JS. . Physical Review. 1956, 104 (6): 1760–1770. Bibcode:1956PhRv..104.1760T. doi:10.1103/PhysRev.104.1760.
  60. Hau, LV; Harris, SE; Dutton, Z; Behroozi, CH. (PDF). Nature. 1999, 397 (6720): 594–598 [2015-05-23]. Bibcode:1999Natur.397..594V. doi:10.1038/17561. （原始内容存档 (PDF)于2012-11-02）.
  61. Liu, C; Dutton, Z; Behroozi, CH; Hau, LV. (PDF). Nature. 2001, 409 (6819): 490–493 [2015-05-23]. Bibcode:2001Natur.409..490L. PMID 11206540. doi:10.1038/35054017. （原始内容存档 (PDF)于2016-04-13）.
  62. Bajcsy, M; Zibrov, AS; Lukin, MD. . Nature. 2003, 426 (6967): 638–41. Bibcode:2003Natur.426..638B. PMID 14668857. arXiv:quant-ph/0311092 可免费查阅. doi:10.1038/nature02176.
  63. Dumé, B. . Physics World. Institute of Physics. 2003 [2008-12-08]. （原始内容存档于2008-12-05）.
  64. Whitehouse, D. . BBC News. 19 July 2000 [2008-12-08]. （原始内容存档于2009-02-21）.
  65. Milonni, PW. . . CRC Press. 2004. ISBN 0-7503-0926-1.
  66. Cherenkov, Pavel A. [Visible emission of clean liquids by action of γ radiation]. Doklady Akademii Nauk SSSR. 1934, 2: 451 （俄语）. Reprinted in Usp. Fiz. Nauk 93 (1967) 385 （页面存档备份，存于）, and in "Pavel Alekseyevich Čerenkov: Chelovek i Otkrytie" A. N. Gorbunov, E. P. Čerenkova (eds.), Moscow, Nauka (1999) pp. 149–153.
  67. Parhami, B. . Plenum Press. 1999: 5. ISBN 978-0-306-45970-2. and Imbs, D; Raynal, Michel. Malyshkin, V , 编. . 10th International Conference, PaCT 2009, Novosibirsk, Russia, August 31 – September 4, 2009. Springer: 26. 2009 [2015-05-23]. ISBN 978-3-642-03274-5. （原始内容存档于2014-09-21）.
  68. 普通光纖的折射率在1.518和1.538之間：Midwinter, JE. 2nd. Krieger Publishing Company. 1991. ISBN 0-89464-595-1.
  69. . Royal Pingdom. Pingdom. June 2007 [2010-05-05]. （原始内容存档于2010-09-02）.
  70. . The Apollo 8 Flight Journal. NASA. [2010-12-16]. （原始内容存档于2011-01-04）.
  71. (新闻稿). Space Telescope Science Institute. 5 January 2010 [2015-05-23]. （原始内容存档于2015-07-25）.
  72. (PDF). NASA. [2010-02-04]. （原始内容存档 (PDF)于2010-02-18）.
  73. . International Astronomical Union. [2010-10-11]. （原始内容存档于2013-06-05）.
  74. 進一步討論請見：. StarChild. NASA. 2000 [2009-08-22]. （原始内容存档于2014-01-29）.
  75. Dickey, JO; et al. . Science. July 1994, 265 (5171): 482–490. Bibcode:1994Sci...265..482D. PMID 17781305. doi:10.1126/science.265.5171.482.
  76. Standish, EM. . Celestial Mechanics. February 1982, 26 (2): 181–186. Bibcode:1982CeMec..26..181S. doi:10.1007/BF01230883.
  77. Berner, JB; Bryant, SH; Kinman, PW. . Proceedings of the IEEE. November 2007, 95 (11): 2202–2214. doi:10.1109/JPROC.2007.905128.
  78. . Financial Times. 10 May 2013 [25 April 2014]. （原始内容存档于2015-05-27）.
  79. . BIPM. 1983 [2009-08-23]. （原始内容存档于2018-06-18）.
  80. Cohen, IB. . Isis. 1940, 31 (2): 327–79. doi:10.1086/347594.
  81. (PDF). Journal des sçavans. 1676: 233–36 [2015-05-23]. （原始内容 (PDF)存档于2011-07-21） （法语）.
    英文譯文：. Philosophical Transactions of the Royal Society. 1677, 12 (136): 893–95. doi:10.1098/rstl.1677.0024.（轉載於Hutton, C; Shaw, G; Pearson, R eds. . 2. London: C. & R. Baldwin. 1809: 397–98.）
    《》中記載的實驗建基於羅默於1676年11月呈交法國科學院的一份報告(Cohen, 1940, p. 346)。
  82. Bradley, J. . Philosophical Transactions. 1729, 35: 637–660 [2015-05-23]. （原始内容存档于2016-02-15）.
  83. Duffett-Smith, P. . Cambridge University Press. 1988: 62. ISBN 0-521-35699-7., Extract of page 62 （页面存档备份，存于）
  84. (PDF). International Astronomical Union. 2012 [2015-05-23]. （原始内容存档 (PDF)于2015-05-01）.
  85. (PDF). International Bureau of Weights and Measures: 14. 2014 [2015-05-23]. （原始内容存档 (PDF)于2015-09-23）.
  86. International Bureau of Weights and Measures, (PDF) 8th: 126, 2006, ISBN 92-822-2213-6 （英语）
  87. Pitjeva, EV; Standish, EM. . Celestial Mechanics and Dynamical Astronomy. 2009, 103 (4): 365–372. Bibcode:2009CeMDA.103..365P. doi:10.1007/s10569-009-9203-8.
  88. IAU Working Group on Numerical Standards for Fundamental Astronomy. . US Naval Observatory. [2009-09-25]. （原始内容存档于2009-12-08）.
  89. . UK National Physical Laboratory. [2009-10-28]. （原始内容存档于2010-08-31）.
  90. Gibbs, P. . Usenet Physics FAQ. University of California, Riverside. 1997 [2010-01-13]. （原始内容存档于2015-08-21）.
  91. Fowler, M. . University of Virginia. [2010-04-21]. （原始内容存档于2015-08-17）.
  92. Cooke, J; Martin, M; McCartney, H; Wilf, B. . American Journal of Physics. 1968, 36 (9): 847. Bibcode:1968AmJPh..36..847C. doi:10.1119/1.1975166.
  93. Aoki, K; Mitsui, T. . American Journal of Physics. 2008, 76 (9): 812–815. Bibcode:2008AmJPh..76..812A. arXiv:0705.3996 可免费查阅. doi:10.1119/1.2919743.
  94. James, MB; Ormond, RB; Stasch, AJ. . American Journal of Physics. 1999, 67 (8): 681–714. Bibcode:1999AmJPh..67..681J. doi:10.1119/1.19352.
  95. Essen, L; Gordon-Smith, AC. . Proceedings of the Royal Society of London A. 1948, 194 (1038): 348–361. Bibcode:1948RSPSA.194..348E. JSTOR 98293. doi:10.1098/rspa.1948.0085.
  96. Rosa, EB; Dorsey, NE. . Bulletin of the Bureau of Standards. 1907, 3 (6): 433. Bibcode:1906PhRvI..22..367R. doi:10.1103/PhysRevSeriesI.22.367.
  97. Essen, L. . Nature. 1947, 159 (4044): 611–612. Bibcode:1947Natur.159..611E. doi:10.1038/159611a0.
  98. Essen, L. . Proceedings of the Royal Society of London A. 1950, 204 (1077): 260–277. Bibcode:1950RSPSA.204..260E. JSTOR 98433. doi:10.1098/rspa.1950.0172.
  99. Stauffer, RH. . The Physics Teacher (American Association of Physics Teachers). April 1997, 35 (4): 231 [2010-02-15]. Bibcode:1997PhTea..35..231S. doi:10.1119/1.2344657. （原始内容存档于2010-02-17）.
  100. . BBC Norfolk website. BBC. [2010-02-15]. （原始内容存档于2007-08-23）.
  101. 有關用干涉法測量光速的詳細討論請見：Vaughan, JM. . CRC Press. 1989: 47, pp. 384–391. ISBN 0-85274-138-3.
  102. Froome, KD. . Proceedings of the Royal Society of London. Series A, Mathematical and Physical Sciences, (The Royal Society). 1958, 247 (1248): 109–122. Bibcode:1958RSPSA.247..109F. JSTOR 100591. doi:10.1098/rspa.1958.0172.
  103. Sullivan, DB. . Lide, DR (编). (PDF). CRC Press. 2001: 191–193. ISBN 0-8493-1247-7. （原始内容 (PDF)存档于2009-08-13）.
  104. Evenson, KM; et al. . Physical Review Letters. 1972, 29 (19): 1346–49. Bibcode:1972PhRvL..29.1346E. doi:10.1103/PhysRevLett.29.1346.
  105. Huygens, C. . Pierre van der Aa. 1690: 8–9 （法语）.
  106. A. A. Michelson. . The Astrophysical Journal. January 1927, 65: 1 [2018-04-02]. ISSN 0004-637X. doi:10.1086/143021. （原始内容存档于2017-09-10） （英语）.
  107. Sarton, G. . Courier Dover. 1993: 248. ISBN 0-486-27495-0.
  108. MacKay, RH; Oldford, RW. . Statistical Science. 2000, 15 (3): 254–78 [2015-05-23]. doi:10.1214/ss/1009212817. （原始内容存档于2016-03-04）.（請點擊目錄中的「Historical background」一章）
  109. Gross, CG. . Neuroscientist. 1999, 5: 58–49. doi:10.1177/107385849900500108.
  110. Hamarneh, S. . Isis. 1972, 63 (1): 119. doi:10.1086/350861.
  111. Lester, PM. . Thomson Wadsworth. 2005: 10–11. ISBN 0-534-63720-5.
  112. O'Connor, JJ; Robertson, EF. . MacTutor History of Mathematics archive. University of St Andrews. [2010-01-12]. （原始内容存档于2009-04-19）.
  113. Lauginie, P. (PDF). . 2005 [2008-07-18]. （原始内容 (PDF)存档于2012-05-27）.
  114. O'Connor, JJ; Robertson, EF. . MacTutor History of Mathematics archive. University of St Andrews. [2010-01-12]. （原始内容存档于2016-05-29）.
  115. Lindberg, DC. . Oxford University Press. 1996: 143. ISBN 0-19-823992-0.
  116. Lindberg, DC. . Edward Grant (编). . Harvard University Press. 1974: 396. ISBN 978-0-674-82360-0.
  117. Marshall, P. . Isis. 1981, 72 (3): 357–74 [367–74]. doi:10.1086/352787.
  118. Florian Cajori, A History of Physics in its Elementary Branches: Including the Evolution of Physical Laboratories （页面存档备份，存于） (1922)
  119. Carl Benjamin Boyer, The Rainbow: From Myth to Mathematics (1959)
  120. Boyer, CB. . Isis. 1941, 33 (1): 24. doi:10.1086/358523.
  121. Galilei, G. . Crew, H; de Salvio A (trans.). Dover Publications. 1954: 43 [1638] [2015-05-23]. ISBN 0-486-60099-8. （原始内容存档于2014-02-03）.
  122. Newton, I. . . 1704 [2015-05-23]. （原始内容存档于2016-02-15）.命題十一的文本在1704年的第一版和1719年的第二版中相同。
  123. Bernhard Riemann, 黎曼全集(第一卷)（簡體書）. . 高等教育出版社. 2016/04/01: 415. ISBN 9787040442618.
  124. Bernhard Riemann. . Annalen der Physik und Chemie. 1867: 237-243.
  125. Graneau, P; Assis, AKT. (PDF). Apeiron. 1994, 19: 19–25 [2010-10-21].
  126. Giordano, Nicholas J. . Cengage Learning. 2009: 787 [2015-05-23]. ISBN 0-534-42471-6. （原始内容存档于2014-09-21）., Extract of page 787 （页面存档备份，存于）
  127. Bergmann, Peter Gabriel. . Courier Dover Publications. 1992: 17 [2015-05-23]. ISBN 0-486-27378-4. （原始内容存档于2014-09-21）., Extract of page 17 （页面存档备份，存于）
  128. Bais, Sander. . Harvard University Press. 2005: 40 [2015-05-23]. ISBN 0-674-01967-9. （原始内容存档于2014-09-21）., Extract of page 40 （页面存档备份，存于）
  129. O'Connor, JJ; Robertson, EF. . School of Mathematics and Statistics, University of St Andrews. November 1997 [2010-10-13]. （原始内容存档于2011-01-28）.
  130. Michelson, AA; Morley, EW. . American Journal of Science. 1887, 34: 333–345. doi:10.2475/ajs.s3-34.203.333.
  131. French, AP. . Van Nostrand Reinhold. 1983: 51–57. ISBN 0-442-30782-9.
  132. Darrigol, O. . Clarendon Press. 2000. ISBN 0-19-850594-9.
  133. Galison, P. . W.W. Norton. 2003. ISBN 0-393-32604-7.
  134. Miller, AI. . Addison–Wesley. 1981. ISBN 0-201-04679-2.
  135. Pais, A. . Oxford University Press. 1982. ISBN 0-19-520438-7.
  136. . BIPM. 1967 [2010-10-13]. （原始内容存档于2011-01-10）.
  137. R.L. Barger, J.L. Hall. . Applied Physics Letters: 196–199. [2018-04-02]. doi:10.1063/1.1654608. （原始内容存档于2022-01-11）.
  138. . BIPM. 1975 [2009-09-09]. （原始内容存档于2008-10-07）.
  139. Taylor, EF; Wheeler, JA. 2nd. Macmillan. 1992. ISBN 0-7167-2327-1.
  140. Penzes, WB. (PDF). NIST. 2009 [2010-01-11]. （原始内容存档 (PDF)于2011-10-19）.
  141. Adams, S. . CRC Press. 1997: 140. ISBN 0-7484-0621-2. One peculiar consequence of this system of definitions is that any future refinement in our ability to measure c will not change the speed of light (which is a defined number), but will change the length of the meter!
  142. Rindler, W. 2nd. Oxford University Press. 2006: 41. ISBN 0-19-856731-6. Note that [...] improvements in experimental accuracy will modify the meter relative to atomic wavelengths, but not the value of the speed of light!
  143. The "explicit-constant" formulation 的存檔，存档日期2014-08-11., BIPM 2011

延伸閱讀

歷史文獻

現代文獻
  • Brillouin, L. . Academic Press. 1960.
  • Jackson, JD. 2nd. John Wiley & Sons. 1975. ISBN 0-471-30932-X.
  • Keiser, G. 3rd. McGraw-Hill. 2000: 32. ISBN 0-07-232101-6.
  • Ng, YJ. . Amelino-Camelia, G; Kowalski-Glikman, J (编). . Springer. 2004: 321ff. ISBN 3-540-25263-0.
  • Helmcke, J; Riehle, F. . Quinn, TJ; Leschiutta, S; Tavella, P (编). . IOS Press. 2001: 453. ISBN 1-58603-167-8.
  • Duff, MJ. . 2004. arXiv:hep-th/0208093 可免费查阅.

外部連結
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.