角動量圖

單一粒子帶有總角動量量子數j與總磁量子數m = j, j − 1, ..., −j + 1, −j，其量子態向量以狄拉克符號的右矢（Ket）標記為|j, m⟩，其圖形則為單箭頭的箭號。有一相對應的左矢（Bra）為⟨j, m|，其圖形為雙箭頭的箭號，指向與右矢相反。

例子中

• 量子數j、m常標記在箭頭附近，以表示特定的角動量量子態，
• 箭頭常在線段的中間
• 等號"="置於等價的圖樣之間，如同相應的代數運算。

最基本的左矢與右矢圖形符號為：

右矢 |j, m⟩

左矢 ⟨j, m|

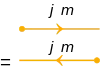
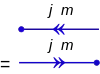
箭號指向頂點或從頂點指出，分別為

• 標準表象（standard representation）以一條離開頂點的指向線段表示，
• 反標準表象（contrastandard representation）則是以一條進入頂點的指向線段表示。

箭號一個一個相接續。在反標準表象中，採用時間反轉算符T。T算符是么正的，也就是其厄米伴算符T^†等於其反算符T⁻¹，即T^† = T⁻¹。其作用在位置算符時，結果保持不變：

${\displaystyle T{\hat {\mathbf {x} }}T^{\dagger }={\hat {\mathbf {x} }}}$

線動量算符則變為負值：

${\displaystyle T{\hat {\mathbf {p} }}T^{\dagger }=-{\hat {\mathbf {p} }}}$

自旋算符也變為負值：

${\displaystyle T{\hat {\mathbf {S} }}T^{\dagger }=-{\hat {\mathbf {S} }}}$

既然軌域角動量算符L = x × p，在T算符作用後也會變為負值：

${\displaystyle T{\hat {\mathbf {L} }}T^{\dagger }=-{\hat {\mathbf {L} }}}$

也因此總角動量算符J = L + S也變為負值：

${\displaystyle T{\hat {\mathbf {J} }}T^{\dagger }=-{\hat {\mathbf {J} }}}$

作用在角動量算符本徵態|j, m⟩，可得：（見註釋）

${\displaystyle T\left|j,m\right\rangle \equiv \left|T(j,m)\right\rangle ={(-1)}^{j-m}\left|j,-m\right\rangle }$

時間反轉的圖形符號為：

時間反轉右矢|j, m⟩.

時間反轉左矢⟨j, m|.

將頂點標記在正確位置相當重要，否則正向時間與反向時間的算符會相互混淆。

狀態|j₁, m₁⟩與狀態|j₂, m₂⟩的內積：

${\displaystyle \langle j_{2},m_{2}|j_{1},m_{1}\rangle =\delta _{j_{1}j_{2}}\delta _{m_{1}m_{2}}}$

相應的圖形符號為：

|j₁, m₁⟩與|j₂, m₂⟩的內積，亦即⟨j₂, m₂|j₁, m₁⟩

時間反轉等價

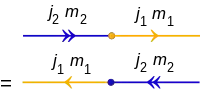
將內積加總，也就是縮併的計算：

${\displaystyle \sum _{m}\langle j,m|j,m\rangle =2j+1}$

習慣上會以一封閉圓來表示，並且標上j：

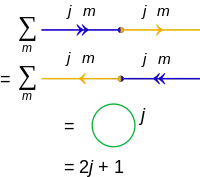內積縮併計算

狀態|j₁, m₁⟩與狀態|j₂, m₂⟩的外積是一算符：

${\displaystyle \left|j_{2},m_{2}\right\rangle \left\langle j_{1},m_{1}\right|}$

相對應的圖形符號為：

|j₁, m₁⟩與|j₂, m₂⟩的外積，亦即|j₂, m₂⟩⟨j₁, m₁|

時間反轉等價

將外積加總，也就是縮併的計算：

${\displaystyle {\begin{aligned}\sum _{m}|j,m\rangle \langle j,m|&=\sum _{m}|j,-m\rangle \langle j,-m|\\&=\sum _{m}{(-1)}^{2(j-m)}|j,-m\rangle \langle j,-m|\\&=\sum _{m}{(-1)}^{j-m}|j,-m\rangle \langle j,-m|{(-1)}^{j-m}\\&=\sum _{m}T|j,m\rangle \langle j,m|T^{\dagger }\end{aligned}}}$

時間反轉算符T的結果可見於上式T|j, m⟩。對外積縮併計算來縮，正向時間與反向時間沒有差別，因此圖形符號表示是相同的，皆為一無指向的線段，其上僅標示j：

外積縮併計算

n狀態|j₁, m₁⟩, |j₂, m₂⟩, ... |j_n, m_n⟩的張量積⊗可寫為：

${\displaystyle {\begin{aligned}\left|j_{1},m_{1},j_{2},m_{2},...j_{n},m_{n}\right\rangle &\equiv \left|j_{1},m_{1}\right\rangle \otimes \left|j_{2},m_{2}\right\rangle \otimes \cdots \otimes \left|j_{n},m_{n}\right\rangle \\&\equiv \left|j_{1},m_{1}\right\rangle \left|j_{2},m_{2}\right\rangle \cdots \left|j_{n},m_{n}\right\rangle \end{aligned}}}$

圖形符號則呈扇形——n項個別態的線段匯聚於一共同頂點。

頂點附近標有一正負號，以表示張量積的順序：

• 負號(−)表示順序為順時針走向${\displaystyle \circlearrowright }$，
• 正號(+)表示順序為逆時針走向${\displaystyle \circlearrowleft }$.

有時候會在正負號之外，加上彎箭頭來表示上述的走向。

|j₁, m₁⟩, |j₂, m₂⟩, |j₃, m₃⟩的張量積，亦即|j₁, m₁⟩|j₂, m₂⟩|j₃, m₃⟩ = |j₁, m₁, j₂, m₂, j₃, m₃⟩

時間反轉等價

兩張量積態的內積：

${\displaystyle {\begin{aligned}&\left\langle j'_{n},m'_{n},...,j'_{2},m'_{2},j'_{1},m'_{1}|j_{1},m_{1},j_{2},m_{2},...j_{n},m_{n}\right\rangle \\=&\langle j'_{n},m'_{n}|...\langle j'_{2},m'_{2}|\langle j'_{1},m'_{1}||j_{1},m_{1}\rangle |j_{2},m_{2}\rangle ...|j_{n},m_{n}\rangle \\=&\prod _{k=1}^{n}\left\langle j'_{k},m'_{k}|j_{k},m_{k}\right\rangle \end{aligned}}}$

|j′₁, m′₁, j′₂, m′₂, j′₃, m′₃⟩與|j₁, m₁, j₂, m₂, j₃, m₃⟩的內積，亦即⟨j′₃, m′₃, j′₂, m′₂, j′₁, m′₁|j₁, m₁, j₂, m₂, j₃, m₃⟩

時間反轉等價

• P.E.S. Wormer, J. Paldus. 51. Elsevier. 2006: 59–124 [2015-03-18]. ISSN 0065-3276. doi:10.1016/S0065-3276(06)51002-0. （原始内容存档于2019-04-11）. |journal=被忽略 (帮助) These authors use the theta variant ϑ for the time reversal operator, here we use T.

• I. Lindgren, J. Morrison. . Chemical Physics 13 2nd. Springer-Verlag. 1986 [2015-03-18]. ISBN 3-540-166-491. （原始内容存档于2015-04-02）.

• G.W.F. Drake. 2nd. springer. 2006: 60 [2015-03-18]. ISBN 0-3872-6308-X. （原始内容存档于2015-04-09）.

• U. Kaldor, S. Wilson. . Progress in Theoretical Chemistry and Physics 11. springer. 2003: 183 [2015-03-18]. ISBN 1-4020-1371-X. （原始内容存档于2015-04-11）.

• E.J. Brändas, P.O. Löwdin, E. Brändas, E.S. Kryachko. 3. Springer. 2004: 385 [2015-03-18]. ISBN 1-402-025-831. （原始内容存档于2015-04-07）.

• P. Schwerdtfeger. . Theoretical and Computational Chemistry 14. Elsevier. 2004: 97 [2015-03-18]. ISBN 008-054-047-3. （原始内容存档于2015-04-07）.

• M. Barysz, Y. Ishikawa. . Challenges and advances in computational chemistry and physics 10. Springer. 2010: 311 [2015-03-18]. ISBN 1-402-099-754. （原始内容存档于2015-04-06）.

• G.H.F. Diercksen, S. Wilson. . Nato Science Series C 113. Springer. 1983 [2015-03-18]. ISBN 9-027-716-382. （原始内容存档于2015-04-10）.

• Zenonas Rudzikas. . . Cambridge Monographs on Atomic, Molecular and Chemical Physics 7. University of Chicago: Cambridge University Press. 2007 [2015-03-18]. ISBN 0-521-026-229. （原始内容存档于2015-04-05）.

• Lietuvos Fizikų draugija. 44. University of Chicago: Draugija. 2004 [2015-03-18]. （原始内容存档于2014-08-19）.

• P.E.T. Jorgensen. . University of Chicago: Elsevier. 1987 [2015-03-18]. ISBN 008-087-258-1. （原始内容存档于2015-04-10）.