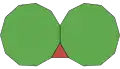
部分截角截四階角五角二十四面體
在幾何學中,部分截角截四階角五角化二十四面體又稱一又二分之一截角五角化二十四面體()是一種凸多面體,具有86個面、228個邊和144個頂點[1],56個等腰三角形、6 正方形和24個十一邊形所組成。其可經由五角二十四面體經過切去四個相鄰面之頂點之後再進行類似截角八面體變換成部分截半截角八面體的操作而構成,是一個八面體群的多面體[2],與其他由五角二十四面體變換來均勻多面體有相同的對稱性[3]。
 | |||||
| 類別 | 擬詹森多面體 | ||||
|---|---|---|---|---|---|
| 對偶多面體 | 會合半截四階角五角化二十四面體 | ||||
| 數學表示法 | |||||
| 施萊夫利符號 | (t)t4g{4,3} | ||||
| 康威表示法 | (t)t4gC | ||||
| 性質 | |||||
| 面 | 86 | ||||
| 邊 | 228 | ||||
| 頂點 | 144 | ||||
| 歐拉特徵數 | F=86, E=228, V=144 (χ=2) | ||||
| 組成與佈局 | |||||
| 面的佈局 | 56個{ }∨() 等腰三角 6個{4} 正方形 24個近似{11} 正十一邊形 | ||||
| 頂點圖 | 3.11.11 3.4.3.11 | ||||
| 對稱性 | |||||
| 對稱群 | O, ½BC3, [4,3]+, 432 | ||||
| 旋轉對稱群 | O, [4,3]+, (432) | ||||
| 特性 | |||||
| 凸 | |||||
| 圖像 | |||||
| |||||
此多面體由56個等腰三角形、6正方形和24個非常接近正十一邊形的十一邊形所組成,其中若等腰三角形和十一邊形換成正三角形和正十一邊形時仍可拼成一個多面體,但會存在十分微小的空隙,在物理上幾乎可以忽略[4][5],類似於拼圖悖論[6],因此此多面體也可以被歸類為擬詹森多面體[7][8][9]。
對偶多面體
部分截角截四階角五角化二十四面體的對偶多面體類似於三角化扭稜立方體,但是其正方形面有類似鳶形多面體截頂截下來之立體的特徵。
| 名稱 | 圖像 | 展開圖 |
|---|---|---|
| 部分截角 截四階角 五角化二十四面體 |
 |
 |
| 它的對偶多面體 |  |
 |
部分截角截四階角五角化二十四面體的對偶多面體共有86個面、228個邊和144個頂點,由120個等腰三角形和24個鳶形所組成。
由於其可以利用五角化二十四面體進行截四階角,但只截一半,即截角時邊長不成比例,使得截出的正方形面比較小,截完後進行康威的會合變換——在每個面加入錐體並使錐高能讓椎體與鄰近面之錐體共面而產生的多面體,因此又稱為會合半截四階角五角化二十四面體。
相關多面體
部分截角截四階角五角化二十四面體與截角十二面體有十分相似的外觀,都有交錯的三角形面,和邊數至少十的多邊形,前者為十一邊形,後者為正十邊形。但他們仍然有十分大的差異,包括前者包含正方形而後者沒有,最大的差異是在其對稱群,前者為八面體群、後者為二十面體群[10],以及後者是半正多面體中的阿基米德立體,但前者僅能歸在擬詹森多面體。
| 名稱 | 部分截角 截四階角 五角化二十四面體 |
截角十二面體 |
|---|---|---|
| 圖像 |  |
 |
| 展開圖 |  |
 |
參考文獻
- Model of Uncompleted truncated tetratruncated pentagonal icositetrahedron (页面存档备份,存于) cgl.uwaterloo.ca [2016-1-9]
- John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, The Symmetries of Things 2008, ISBN 978-1-56881-220-5
- Coxeter Regular Polytopes, Third edition, (1973), Dover edition, ISBN 0-486-61480-8 (pp. 145–154 Chapter 8: Truncation)
- Kaplan, Craig S.; Hart, George W., , (PDF), 2001 [2016-01-08], (原始内容存档 (PDF)于2015-09-23).
- Joseph O’Rourke.Computational Geometry in C. Cambridge University Press, 2 edition, 1998.
- Luchins, A. S. (1942). Mechanization in problem solving. Psychological Monographs, 54, No. 248.
- Near Misses (页面存档备份,存于) last one cgl.uwaterloo.ca [2016-1-7]
- Daniele Barbaro. La Pratica Della Perspettiva. 1569. Arnaldo Forni reprint, 1980. [2016-1-8]
- Craig S. Kaplan and George W. Hart. Symmetrohedra: Polyhedra from Symmetric Placement of Regular Polygons (页面存档备份,存于). In Bridges 2001: Mathematical Connections in Art, Music and Science, 2001.
- Sir William Rowan Hamilton, (PDF), Philosophical Magazine, 1856, 12: 446 [2016-01-09], (原始内容存档 (PDF)于2016-03-04)
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.