非线性偏微分方程
非线性偏微分方程是具有非线性项的偏微分方程。起源於各種應用科學中,如固體力學、流體力學、聲學、非線性光學、等離子體物理學、量子場論等學科。它们描述了许多不同的物理系统,并被用于解决数学问题,如庞加莱猜想和卡拉比猜想。它们很难研究:几乎没有通用的技术可以用于所有这样的方程,通常每个单独的方程都必须作为一个单独的问题进行研究。通常,线性和非线性偏微分方程的区别是基于定义偏微分方程本身的算子的属性。
| 微分方程 |
|---|
 |
| 分類 |
| 解 |
函數關係 F(,x_1,X_2..x_n,u,u_x1,u_x2..u_xn,u_x1x2,u_x1x3...)=0 是一個廣義的偏微分方程,如果 u,v 是此微分方程的兩個解,而(au+bv) 也是此微分方程的解,則此偏微分方程稱為線性偏微分方程,否則稱為非線性偏微分方程。[1]
常見的非線性偏微分方程
| Equation | 中文 | 方程 | 图 | ||
|---|---|---|---|---|---|
| BBM | 班傑明-小野方程 | : | 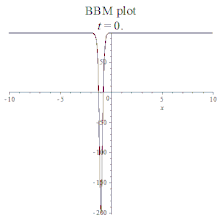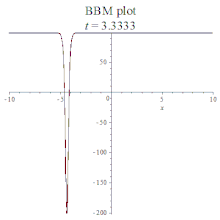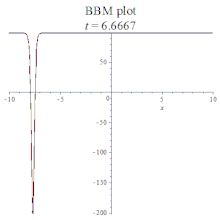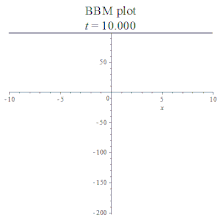 | ||
| Belousov-Zhabotinsky | 别洛乌索夫-扎伯廷斯基方程 | ,
|  | ||
| (Benjamin-Ono equation | 本杰明-小野方程 | 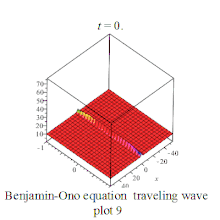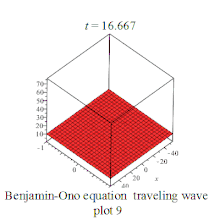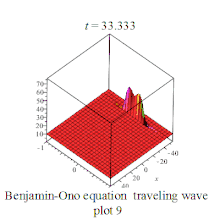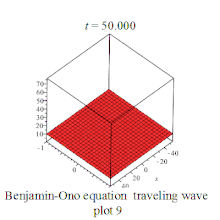 | |||
| Bogoyavlenski-Konoplechenko | 波格雅夫连斯基-科譳普勒琛科方程 |  | |||
| Born-Infeld | 玻恩-英费尔德方程 |  | |||
| Boussinesq | 博欣内斯克方程 |  | |||
| Boussinesa type | 博欣内斯克型方程 |  | |||
| Unnormalized Boussinesq | 非规范博欣内斯克方程 |  | |||
| Broer-Kaup | 布罗尔-库普方程组 |
|  | ||
| Burgers | 伯格斯方程 |  | |||
| Burgers-Fisher | 伯格斯-费希尔 方程 | : |  | ||
| Modified Burgers | 变形伯格斯方程 |  | |||
| Unnormalized Burgers | 非规范伯格斯方程 |  | |||
| Generalized Burgers | 广义伯格斯方程 | ||||
| Burgers-Huxley | 伯格斯-赫胥黎方程 |  | |||
| Bretherton | 布雷瑟顿方程 | 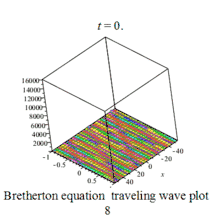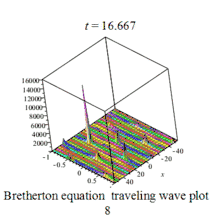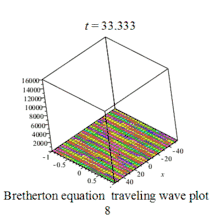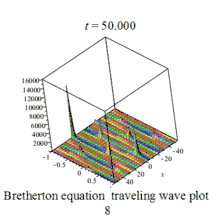 | |||
| Cahn-Hilliard | 卡恩-希利亚德方程 | ||||
| Cassama-Holm | 卡马萨-霍尔姆方程 | : | 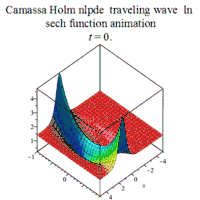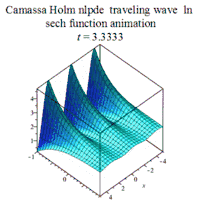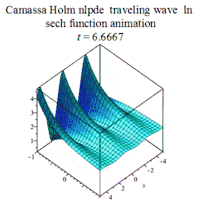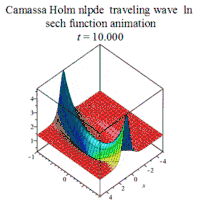 | ||
| Chaffee-Infante | 查菲 - 堙方特方程 |  | |||
| Chaplygin | 查普里金方程 | 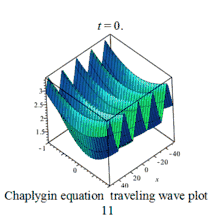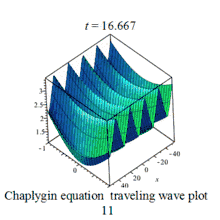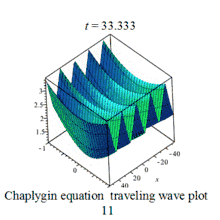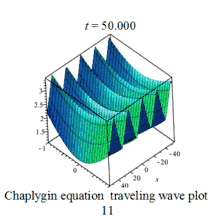 | |||
| Davey–Stewartson | 戴维-斯图尔森方程组 | :
| 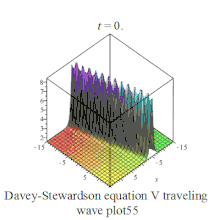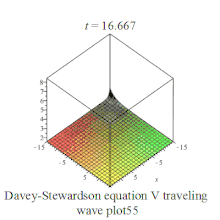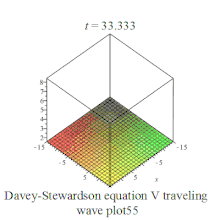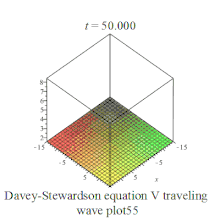 | ||
| Degasperis-Procesi | DP 方程 |  | |||
| Drinfeld-Solokov-Wilson | DSW 方程 |
|
 | ||
| Dodd-Bullough-Mikhailov | 多德-布洛-米哈伊洛夫方程 | [[ |  | ||
| Nonlinear Diffusion | 非线性扩散方程 |  | |||
| Harry Dym | 迪姆方程 | : | 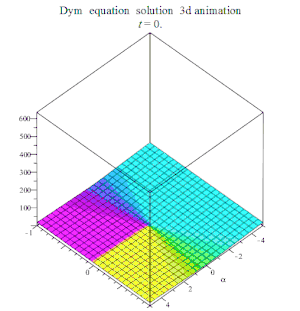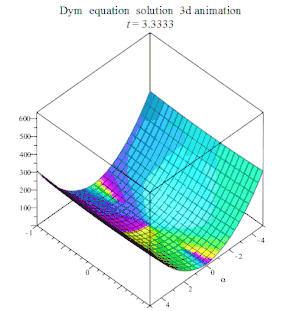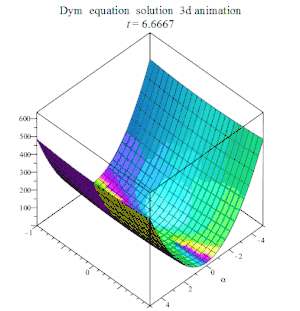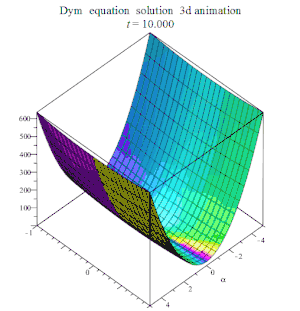 | ||
| Eckhaus | 艾克豪斯方程 |
|
 | ||
| Eikonal | 程函方程 | 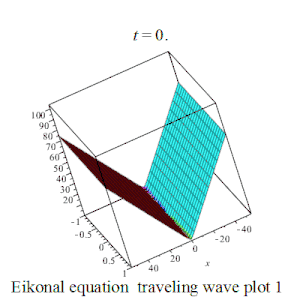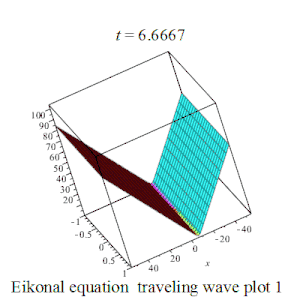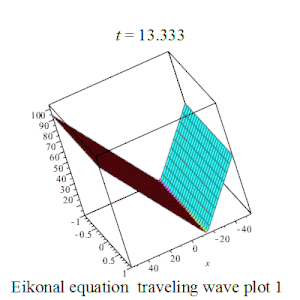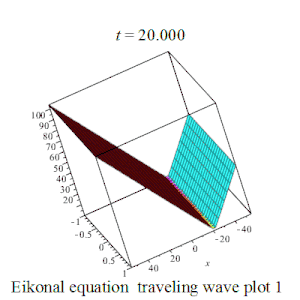 | |||
| Estevez-Mansfield-Clarkson | 埃斯特韦斯-曼斯菲尔德-克拉克森方程 |  | |||
| Fitzhugh-Nagumo | 菲茨休 - 南云方程 | 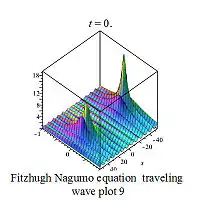 | |||
| Fisher | 费希尔方程 | 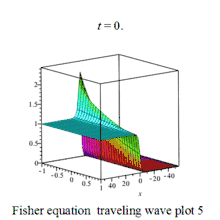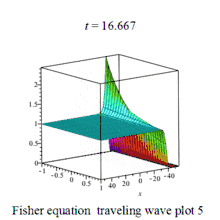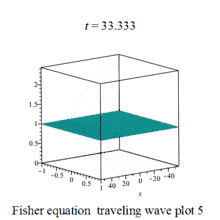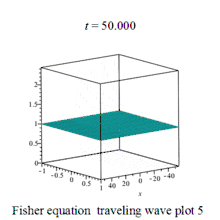 | |||
| Fisher-Kolmogorov | 费希尔-柯尔莫哥洛夫方程 | :: |  | ||
| Fujita-Storm | 藤田-斯托姆方程 |  | |||
| Gardner | 加德纳方程 |  | |||
| Gibbons-Tsarev | 吉本斯-查理夫方程 |  | |||
| Ginzburg-Landau | 金兹堡-朗道方程 |  | |||
| Hirota Satsuma | 广田-萨摩方程组 | :
|
 | ||
| Hunt-Saxton | 亨特 - 萨克斯顿方程 | : |  | ||
| Ito | 伊藤方程 |  | |||
| KdV | KdV方程 | : |  | ||
| Modified KdV | MKdV方程 |  | |||
| KdV-mKdV | KdV-mKdV方程 |  | |||
| KdV-Burgers | KdV-Burgers方程 | 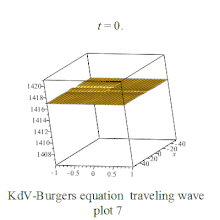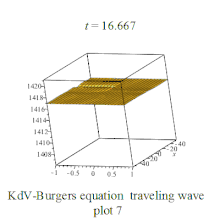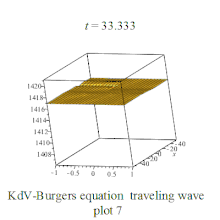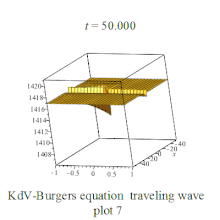 | |||
| Modified KdV-Burgers | 变形KdV-Burgers方程 | 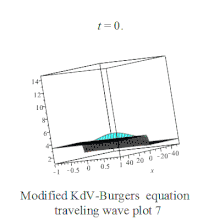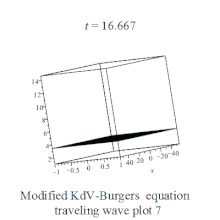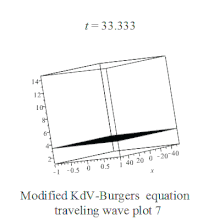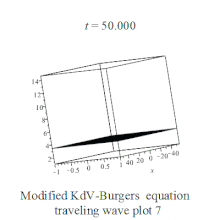 | |||
| Fifth order KdV | 五阶KdV方程 |  | |||
| Fifth order dispersion KdV | 五阶色散KdV方程 |  | |||
| Seventh order KdV | 七阶KdV方程 | 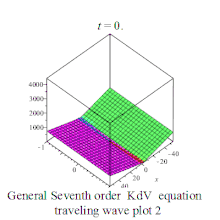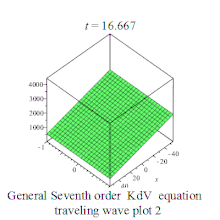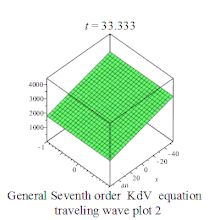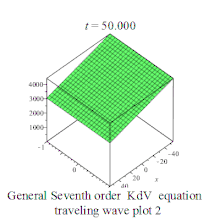 | |||
| Nineth order KdV | 九阶KdV方程 | 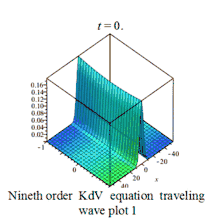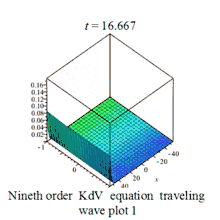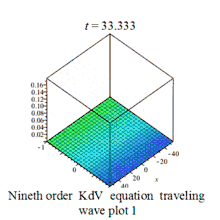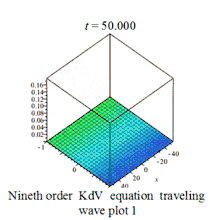 | |||
| Unnormalized KdV equation | 非规范KdV方程 |  | |||
| Generalized Burgers-KdV | 广义伯格斯-KdV方程 |  | |||
| Unnormalized modified KdV | 非规范变形KdV方程 |  | |||
| von Karman | 冯·卡门方程 |
|  |
參考文獻
- Inna Shingareva Carlos Lizarrga Celaya, Solving Nonlinear Partial Differential Equations with Maple and Mathematica, Springer, ISBN 9783709105160
- *谷超豪 《孤立子理论中的达布变换及其几何应用》 上海科学技术出版社
- *阎振亚著 《复杂非线性波的构造性理论及其应用》 科学出版社 2007年
- 李志斌编著 《非线性数学物理方程的行波解》 科学出版社
- 王东明著 《消去法及其应用》 科学出版社 2002
- *何青 王丽芬编著 《Maple 教程》 科学出版社 2010 ISBN 9787030177445
- Andrei D. Polyanin,Valentin F. Zaitsev, HANDBOOK OF NONLINEAR PARTIAL DIFFERENTIAL EQUATIONS, SECOND EDITION CRC PRESS
- Graham W. Griffiths William E.Shiesser Traveling Wave Analysis of Partial Differential p135 Equations Academy Press
- Richard H. Enns George C. McCGuire, Nonlinear Physics Birkhauser,1997
- Inna Shingareva, Carlos Lizárraga-Celaya,Solving Nonlinear Partial Differential Equations with Maple Springer.
- Eryk Infeld and George Rowlands,Nonlinear Waves,Solitons and Chaos,Cambridge 2000
- Saber Elaydi,An Introduction to Difference Equationns, Springer 2000
- Dongming Wang, Elimination Practice,Imperial College Press 2004
- David Betounes, Partial Differential Equations for Computational Science: With Maple and Vector Analysis Springer, 1998 ISBN 9780387983004
- T.Roubicek: Nonlinear Partial Differential Equations with Applications, 2nd ed., Birkhäuser, Basel, 2013, ISBN 978-3-0348-0512-4.
- George Articolo Partial Differential Equations & Boundary Value Problems with Maple V Academic Press 1998 ISBN 9780120644759
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.