AdS/CFT对偶

人們現時對重力的理解基於阿爾伯特·愛因斯坦的廣義相對論[6]。於1915年成形的廣義相對論，用時間與空間（即時空）的幾何來解釋重力。它所用的語言是古典物理學[7]，是由艾薩克·牛頓及詹姆斯·麥克斯韋等物理學家所開發的。而其他非重力的作用力則由量子力學的框架來解釋。量子力學是在二十世紀前半葉由许多位物理學家建立的，用概率來描述物理現象，與之前的經典物理學完全不一樣[8]。

探索如何使用量子力學原則來描述重力的物理學分支就是量子重力。現時，最受關注的量子重力的方法是弦理論[9]，弦理論不使用零維的點粒子，而改用一維物體──弦來作为基本粒子的模型。在對偶中，通常考虑的是从弦理论或其现代延伸M理论导出的量子引理[10]。

人們日常生活中所熟悉的空間有三維（上下、左右及前後），還有一維時間。因此用現代科學的語言，會說時空是四維的[11]。弦理論和M理論有一個很奇怪的特點，就是時空需要額外的維度，以保证數學上的一致性：在弦理論中時空有10維，而在M理論中則有11維[12]。在AdS/CFT对应中，量子引力理论通常是从弦理论和M理论中通过紧致化的过程得到的。緊化能夠減低理論的有效時空维數，將多餘的維度“卷曲”成圓圈[13]。

緊緻化可以通過考慮多維物件來解釋，如橡膠水管。如果從足夠距離外看橡膠水管的話，它看起來就只有一維，就是長度。然而，向水管靠近的話，就會發現它的第二維圓周。因此在橡膠水管中爬行的螞蟻能在两个维度上移动[14]。

一些物體具有時間空間範圍，如電磁場等，而應用在這些物體上的量子力學就是量子場論[15]。量子場論是粒子物理學研究基本粒子的基礎理論，而其中這些粒子由基本場的激發所描述。而凝聚態物理學也會使用量子場論來模擬類似於粒子的準粒子[16]。

使用對偶時，除了要考慮量子重力理論外，還需要考慮某一種叫共形場論的量子場論。它是一種對稱性強且数学性质良好的量子場論[17]。這種理論包括兩種應用，一是弦理論，用於描述弦傳播時所掃出的表面；二是統計力學，用於处在熱力學臨界點的系统的模型[18]。

在對偶中要考慮的是在反德西特背景上的弦理論或M理論。亦即是說其空間幾何是由愛因斯坦方程的一種真空解所描述，称为反德西特空间。

用简单的话来说，反德西特空間是时空的一种數學模型，其中點與點間的距離概念（度規），與通常的歐幾里德幾何中的距離概念不一樣。反德西特空間與双曲空间有着密切的關係，而雙曲空間可用右圖的圓盤表示[19]。右圖為由三角形和正方形所組成的密鋪。用某種方式可以為點間的距離下定義，使得所有三角形和正方形都是一樣大小的，並且圓周的外邊界與其內部任一點的距離為無限[20]。

現在想像一疊雙曲圓盤，其中每一片圓盤代表某時間的宇宙態。而由此形成的幾何物體就是三维反德西特空間[19]。它看起來像實心的圓柱體，其中每一片截面都是雙曲圓盤。下圖中垂直方向代表時間。這个圓柱體的表面在對偶中有着重要的角色。反德西特空間跟雙曲平面一樣，它的彎曲方式使得內部任何一點與邊界面的距離為無限遠[21]。

三維的反德西特空間就像是一疊雙曲圓盤，每一片圓盤代表某時間的宇宙態。而由此形成的時空看起來就像一个实心圓柱體。

這樣的結構雖然描述了只有二維空間加一維時間的假想宇宙，但是可以推廣至任何維數。雙曲空間實際上是可以超過二維的，把這些雙曲空間疊起來就能形成反德特空間的高維度模型[19]。

反德西特空間的重要特點在於其邊界（三維德西特空間的邊界看起來像圓柱體）。這種邊界有一個特性，就是在任何點的局部範圍都和閔考斯基時空很像，而閔考斯基時空就是非重力物理所用的時空模型[22]。

因此可以構建一套“時空”就是反德西特空間的邊界的輔助理論。而這項觀察正是對偶的出发点，因為對偶把反德西特空間的邊界視為共形場論的“時空”。對偶主張共形場論等价于反德西特空間中的重力理論，也就是說兩者可以像有“字典”的那樣把一个理论中的计算翻译为另一个理论中的计算。一套理論中的每一个对象在另一套理論中都有對應。比方說，重力理論中的單一粒子可能對應邊界理論中的某堆粒子。此外，兩套理論的预测在数量上也是相等的，例如說重力理論中兩個粒子碰撞的概率是40%，那麼共形場論的對應粒子堆碰撞概率也會是40%[23]。

圖為一幅二維全息圖，當中儲存了所代表物體的三維信息。上下兩幅圖畫為從不同角度拍攝的同一張全息圖。

要注意的是，反德西特空間邊界的維度比反德西特空間本身的要低。比方說，上文的三維例子，其邊界為二維表面。由於兩理論間的關係就像三維物件與全息圖形象的關係，所以對偶是一種“全息對偶”[24]。雖然全息圖是二維的，但是它儲存了所代表物體的三維信息編碼。對偶也是一樣，雖然它所聯繫的兩套理論存在於不同維數的時空，但是對偶假定它們是完全等价的。共形場論就像是全息圖，捕捉了較高維數的量子重力理論信息[20]。

自1997年馬爾達西那發表了他的洞察以來，理論物理學家發現了不少對偶的各种实例。它們把各種共形場論與各種維數的弦理論和M理論的緊緻化聯繫起來。儘管一般來說要使用這些理論來模擬真實世界並不可行，但是它們卻具有一些對解決量子場論和量子重力難題有用的特點，例如所含有的粒子和高度的對稱性[25]。

對偶最有名的例子，就是積空間${\displaystyle AdS_{5}\times S^{5}}$上的IIB型弦理論等价于於四維邊界上的N=4超对称杨-米尔斯理论[26]在這個例子中，引力理論所處的時空實際上為五維（因此標記為${\displaystyle AdS_{5}}$），还有五个额外的紧致维度（由因子${\displaystyle S_{5}}$所代表）。至少在宏觀角度上，真實世界中的時空為四維，因此這個版本的對偶並不能真實地模擬重力。同樣地，由於對偶理論假定大量的超對稱性，因此也不適合模擬任何的真實世界系統。然而，如下文所解釋，這種邊界理論的一些特徵與強相互作用的基礎理論量子色動力學一致。其所描述的粒子與量子色動力學的膠子類似，同時還描述了某些費米子[9]。因此，這種理論能應用於核物理，尤其是用於研究夸克-膠子漿[27][28]。

這項對偶的另一種实现，為${\displaystyle AdS_{7}\times S^{4}}$上的M理論等价于六維時空上的(2,0)理论[2]。在這個例子中，重力理論的時空實際上為七維。出現在此對偶一端的(2,0)理論，其存在由超共形场论的分類所預測。由於(2,0)理論是一種沒有經典極限的量子力學理論，所以物理學家對它仍然缺乏理解[29]。儘管研究這種理論有其固有的難度，但是從數學與物理的各種理由出發，它還是一個相當有意思的研究課題[30][31]。

這項對偶的又一種實踐，為${\displaystyle AdS_{4}\times S^{7}}$上的M理論等价於三維的ABJM超共形场论[32]。這裏的重力理論有四維的非緊化時空，因此這個版本的對偶能提供某程度上比較真實的重力理論[33]。

量子世界裏的相互作用：點粒子的世界線（左）或由弦理論中的閉弦所掃出的世界面（右）。

使用量子場論計算各種物理事件的概率時，一般需要用到微擾理論。微擾量子場論由理查德·費曼及其他物理學家於二十世紀前半葉開發，這項理論使用費曼圖來整理計算。費曼圖所代表的是點粒子的路徑與相互作用[15]。儘管這種體系對於預測而言非常有用，但是這些預測只能在相互作用強度（由耦合常數所描述）足夠小的時候才有效，即微擾理論只能描述弱到近乎不存在的相互作用[34]。

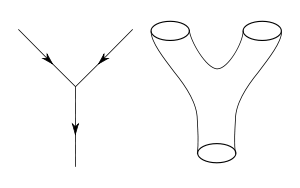
弦理論的出发点在於量子場論的點粒子可由一維的弦所描述。弦的相互作用的定义大多直接由量子場論的微擾理論推廣得到。若從費曼圖的視點出發，則意味着把代表點粒子路徑的一維圖，換成代表弦運動的二維表面（見右圖）。跟量子場論不同的是，弦理論並未有全面的非微擾定義，因此弦理論還是不能解答許多物理學家想問的問題[35]。

研究對偶的其中一個最初動機，就是解決開發弦理論非微擾表述這道難題[36]。如上文所釋，對偶為量子場論的幾種例子提供了等價的反德西特空間弦理論。對於重力場為漸近反德西特的特例（即在無限遠時重力場類似於反德西特空間上的），這種對偶可被視為給出弦論的定義。弦理論中受關注的物理量的定義皆由對偶量子場論的物理量來定義[20]。

史蒂芬·霍金於1975年發表了一份計算，指出黑洞並非全黑，還是會射出暗淡輻射的，而成因則為事件視界附近的量子效應[37]。由於起初霍金的結果指出黑洞會催毀信息，因此成了理論界的難題。更精確地來說，霍金的計算似乎是違反了一條量子力學的基本假设，即物理系統的時間演化需遵守薛定諤方程。這項特性一般被稱為時間演化的么正性。霍金的計算與量子力學么正性假设間的表面衝突，後來被稱為黑洞信息悖論[38]。

對偶在某程度上成功解決了黑洞信息悖論，因為它能表明黑洞的時間演化是如何能在某程度上遵行量子力學。用對偶的內容來考慮黑洞是確實可行的，任何此類黑洞都對應一系列位處反德西特空間邊緣的粒子[39]。這些粒子正常地遵從量子力學的規則，特別是么正性時間演化，因此黑洞也必須符合么正性時間演化，遵守量子力學的規則[40]。霍金於2005年承認悖論以所得的信息守恆告終，並提出了一個黑洞是如何保存信息的具體可行機制[41]。

其中一個用對偶研究過的物理系統就是夸克-膠子漿，它是由粒子加速器所產生的一種奇異物質狀態。當如金或鉛核等重離子在短暫的瞬間以高能量對撞時會產生這種狀態。如此的碰撞使得組成原子核的夸克退禁闭，而退禁閉時溫度約為二萬億開爾文，情況與大霹靂後${\displaystyle 10^{-11}}$秒時相若[42]。

夸克-膠子漿的物理由量子色動力學所支配，但這理論在數學上並不能夠對付夸克-膠子漿的相關難題[43]。譚青山（Đàm Thanh Sơn）與協作者與2005年的一份論文中，成功表明可以使用對偶將難題轉成弦理論的語言，來研究夸克-膠子漿的某些方面[27][28]。譚青山與協作者通過應用對偶，利用五維時空的黑洞來描述夸克-膠子漿。計算中證明了夸克-膠子漿的兩個物理量──剪切黏度${\displaystyle \eta }$和熵的體密度${\displaystyle s}$兩者之間的比值約為某通用常數：

${\displaystyle {\frac {\eta }{s}}\approx {\frac {\hbar }{4\pi k}}}$

其中${\displaystyle \hbar }$為約化普朗克常數，${\displaystyle k}$則為玻耳兹曼常數[44][28]。此外，作者還在論文中推測此通用常數就是多個系統中${\displaystyle \eta /s}$的下界。布魯克黑文國家實驗室的相对论性重离子对撞机於2008年確認了比率的預測值[45]。

夸克-膠子漿的另一重要特點就是在漿中移動的超高能量夸克會在僅僅數飛米的距離內被停止或“冷卻”。此現象由噴流冷卻參數${\displaystyle {\hat {q}}}$所描述，該參數將夸克的能量流失與其漿內運動距離的平方聯繫起來。基於對偶的計算使得理論物理學家能夠估算出${\displaystyle {\hat {q}}}$，並且所得的計算值與參數的測量值大致吻合，因此間接表明對偶可能有助於更深入的研究[44]。

圖為在高溫超導體上懸浮的磁鐵。現在的物理學家有使用對偶來研究高溫超導現象。[46]

研究凝聚態的實驗物理學家在過去的數十年間發現了多種奇異的物質狀態，包括超導體和超流體。儘管這些狀態由量子場論的框架來描述，但使用標準場論技巧還是很難去解釋某些現象。包括蘇比爾·薩克達夫在內的一些凝聚態物理學家期望對偶能讓使用弦理論語言描述這些系統變得可行，從而可以更深入地研究它們的性質[27]。

以弦理論方法描述超流體至絕緣體的過渡至今已取得一定的成果。超流體是一種流動時沒有摩擦力的中性原子系統。這樣的系統一般在實驗室中用液態氦製作，但近年實驗物理學家開發了新的人工超流體製作方式：將數以萬億計的冷原子倒入十字交叉的雷射晶格中。這些原子最初相當於超流體，但當實驗者增大雷射強度時，原子的活動量下降，並突然過渡成絕緣態。原子在過渡途中會出現反常狀態。例如，原子會以一定的速率慢慢停止，而這個速率取決於溫度和普朗克常數，後者為量子力學的基礎參數，並不會出現在其他相的描述中。這樣的表現在近年才從對偶描述中得到解答，在描述中流體的特性以高維度黑洞來描述[47]。

不少物理學家都轉而採用弦理論方法去對付核物理和凝聚態物理學的難題，而一些研究這些領域的理論物理學家則對對偶是否能成為模擬真實世界系統的工具這一點提出質疑。拉里·麥里蘭（）於2006年的夸克物質研討會中[48]，指出對偶中的N=4超對稱楊-米爾斯理論與量子色動力學有顯著差別，因此將這些方法應用於核物理是件難事。據麥里蘭所說：

${\displaystyle {\mathcal {N}}=4}$超楊-米爾斯理論不是量子色動力學……它沒有質量尺度，又具有共形不變性。它既沒有禁閉，也沒有巡行耦合常數。它具有超對稱性。它既沒有手徵對稱破壞，又沒有質量生成機制。它的伴隨表示有六種純量粒子和費米子……修正上述所有或一部份的問題或許是可行的，否則對某些物理問題來說這些相異點是會構成影響的。對於假想是否能保證${\displaystyle {\mathcal {N}}=4}$超楊-米爾斯理論能真實地反映量子色動力學，或存在其他有相同功效的物理現象，到目前為止仍然未有共識，或任何令人信服的證據[48]。

諾貝爾物理學獎得主菲利普·安德森在致《今日物理》雜誌的一封信中，也表達了對於對偶的凝聚態應用的近似憂慮，其中寫道： 在给《今日物理》雜誌的一封信中，诺贝尔物理学奖获得者菲利普·安德森写道：

作為凝聚態理論中的手法有一個非常普遍的問題，我們可以指向那三個告密的英文字母“”──共形場論。凝聚態問題一般來說既不是相對論性，也不是共形的。在臨近量子臨界點時，時間和空間可能會有縮放，但即使如此我們還是有更熟悉的座標系，一般是晶格。有證據顯示奇異金屬左側存在其他線性T相，至於是甚麼就歡迎猜測了，但在這種情況凝聚態問題還是由實驗事實所超定的[49]。

物理學家在很早之前就已經着手研究弦理論與核物理間的關係，而在1997年末的發現就是這方面長年所積累的成果[50]。實際上，弦理論最初在1960年代末至1970年代初被提出時，是用於描述強子的，強子指的是由強相互作用牽引的次原子粒子，如質子和中子。弦理論把每一種的這些粒子視為弦的不同振蕩模式。實驗物理學家在1960年代末就已經發現，強子符合某一類的雷吉軌跡，這種軌跡的能量平方與其角動量成正比；而後來理論物理學家則指出，從旋轉相對論性弦的物理中，會自然地出現如此的關係[51]。

而另一方面，在把強子視作弦的嘗試中發現了多個嚴重的難題。其中一個就是弦理論中包括無質量且自旋為2的粒子，而在強子物理中尚未有對應的粒子[52]。這樣的粒子所傳遞的力會有着重力的特性。喬爾·謝克和约翰·施瓦茨因此於1974年提出弦理論不是理論物理學家以為的核物理理論，而是量子重力理論[53]。與此同時，物理學家發現了強子實際上是由夸克所組成的，因此他們放棄了用弦理論的手法研究強子，而改為採用量子色動力學。

夸克在量子色動力學中有一種荷具有三種類型，叫色荷。傑拉德·特·胡夫特於1974年的論文中，以近似量子色動力學的觀點來研究弦理論與核物理間的關係，當中所用的色荷數為${\displaystyle N}$，而不是三。在這篇論文中，特·胡夫特考慮了當${\displaystyle N}$趨向無限時的某個極限，並表明在這個極限時某些量子場論的計算與弦理論的計算類似[54]。

史蒂芬·霍金於1975年預測黑洞會因量子效應而射出輻射。

史蒂芬·霍金於1975年發表了一份計算，指出黑洞並非全黑，還是會射出暗淡輻射的，而成因則為事件視界附近的量子效應[37]。之前雅各布·貝肯斯坦在研究就指出過黑洞熵的定義良好[55]，而霍金的研究正是這份研究的後續。霍金的結果最初看起來違反了量子力學的基本假想，即時間演進的么正性。么正性假想直覺上所說的是，量子系統並不會因為態與態之間的演進而將信息毀滅。因此，這項表面上的衝突被稱為黑洞信息悖論[38]。

李奧納特·蘇士侃對開發量子重力中全息原理的初期作出過貢獻。

傑拉德·特·胡夫特在後來的1993年撰寫了一篇具猜想性的論文，其中以量子重力的觀點，重新檢視霍金的黑洞熱力學研究，結論為圍繞黑洞的時空自由度總數與視界的表面積成正比[56]。這個概念被李奧納特·蘇士侃改良及提倡，成就了現時的全息原理[57]。全息原理及其通過在弦理論中的實踐，不單對闡明由霍金的研究延伸出的黑洞奧秘有重大作用，而且也為黑洞信息悖論提供了一個讓專家信服的可能解答[58]。霍金於2004年承認黑洞確實不違反量子力學[59]，他同時亦提出了一個黑洞是如何保存信息的具體可行機制[41]。

胡安·馬爾達西那於1997年末發表了一篇具里程碑意義的論文，就此觸發了這一個研究領域[2]。據亞歷山大·泊里雅科夫的說法，那篇論文就是“開啟水閘的研究”[60]。這個猜想馬上就引發了弦理論研究界的濃厚興趣[40]，不久後就有兩篇認真檢視這個對偶的論文，一篇史蒂芬·格布瑟、伊戈爾·克列巴諾夫和亞歷山大·泊里雅科夫合著[3]，另一篇則由愛德華·威滕所撰寫[4]的論文。這兩篇論文使得馬爾達西那的猜想更加明確，並成功證明了對偶中的共形場論是位於反德西特空間的邊界[61]。

胡安·馬爾達西那最早於1997年末提出對偶。

馬爾達西那的對偶中有一項特例，就是${\displaystyle {\mathcal {N}}=4}$超楊-米爾斯理論與五維反德西特空間的弦理論是相等的[32]，而楊-米爾斯理論則是一種與量子色動力學相近的規範場論。這個結果有助於釐清特·胡夫特之前有關弦理論與量子色動力學間關係的研究，並把弦理論帶回以前作為核物理理論的根源[51]。

核物理學家譚青山在1999年開始了在哥倫比亞大學的工作後，就去探望同在紐約的本科時期友人安德烈·斯塔里內特斯（Andrei Starinets），他當時正在紐約大學攻讀弦理論博士學位的[62]。儘管當時二人並沒有合作研究的打算，但是譚青山很快就意識到斯塔里內特斯的計算能釐清夸克-膠子漿的一些性質，而夸克-膠子漿是重離子在高能碰撞下的產物。譚青山在與斯塔里內特斯和帕維爾·柯夫頓（Pavel Kovtun）的合作下，成功使用對偶計算出夸克-膠子漿的一個重要參數[27][28]。譚青山後來憶述時說；“為了計算出夸克-膠子漿的剪切黏度數值，我們完全改變了整個計算……我其中一位研究核物理的朋友開玩笑說，我們的論文是弦理論的第一份實用論文[27]。”

時至今日，物理學家仍繼續在量子場論中為對偶發掘新應用[46][63]。除了由譚青山及同事所提倡的核物理應用，其他如蘇比爾·薩克達夫的凝聚態物理學家已經在使用弦理論方法去研究凝聚態物理學的某些方面。其中一個這方向的重要成果，就是成功經由對偶描述了超流體到絕緣體的過渡[47]。此外還有另一項新興的研究課題：流體/重力對偶，其中使用了對偶來將流體動力學的問題轉譯成廣義相對論的問題[64]。

為了能更清楚瞭解四維宇宙重力的量子效應，有些物理學家對於維度較低的數學模型做研究，其中有兩維空間及一維時間[65]。描述重力場的數學在這樣的設定下變得簡單得多，這樣就可以使用熟悉的量子場論來研究量子重力，也就不需要出動弦理論或其他更尖端的手法來研究四維的量子引力[66]。

始於J·D·布朗和馬克·昂諾在1986年的研究[67]，物理學家意識到三維時空的量子重力與二維的共形場論有着密切的關係。昂諾與同事於1995年更仔細地研究這種關係時，提出反德西特空間的三維重力相等於一種叫劉維爾場論的共形場論[68]。另一項由愛德華·維滕提出的假想指出，反德西特空間的三維重力相等於具怪獸群對稱的共形場論[69]。這些假想就是場論不需要全套弦理論或M理論的證據[70]。

現今宇宙會以愈來愈快的速度膨脹，而反德西特空間則與現今宇宙不一樣──反德西特空間既不會膨脹，也不會收縮。它的大小在任何時間看起來都一樣[19]。用較專門的術語來說，就是反德西特空間對應宇宙學常數為負的宇宙，而現今宇宙的宇宙學常數是一個微小的正數[71]。

儘管在短距離上重力與宇宙學常數的值應該沒有很大的關聯[72]，但是能讓有一個宇宙學常數為正的版本還是一件好事。安德魯·施特罗明格於2001年引入了對偶的新版本，叫dS/CFT對偶[73]。這項對偶的時空模型叫德西特空間，其宇宙學常數為正。從宇宙學的觀點來看，由於許多宇宙學家認為極早期的宇宙與德西特空間相近，因此這樣的對偶是非常有意思的[19]。現今宇宙在遙遠的未來也可能會與德西特空間類似[19]。

儘管對於研究黑洞性質是有用的[74]，但是大部份用對偶所考慮的黑洞在物理上並不現實。實際上就如上文所解釋，大部份的版本都需要用到帶非自然對稱的多維時空模型。

莫妮卡·桂卡（）、托馬斯·哈特曼（）、宋伟（）和安德魯·斯特羅明格於2009年成功證明對偶還是可以用於研究天體物理學的黑洞。這項結果更精確地來說是可用於接近極值克爾黑洞的黑洞，這種黑洞的單位質量角動量是最大的[75]。他們成功證明這種黑洞能用相等的共形場論表示。克爾/CFT對偶後來延伸到角動量較低的黑洞[76]。

對偶與另一對偶有着密切的關係，那個對偶是由伊戈爾·克列巴諾夫和亞歷山大·泊里雅科夫於2002年所推測的[77]。該對偶指出反德西特空間中的某“高自旋規範場論”相等於帶O(N)對稱的共形場論。這理論的本體是一種描述任意高自旋粒子的規範場論。它於弦理論相近，因為弦的激發態可對應高自旋粒子。因此該對偶可能有助於研究對偶的弦理論版本，和甚至可能證明對偶[78]。西蒙尼·瓊比（）和尹希（）於2010年透過計算三點函數獲得了更多該對偶的證據[79]。