三角形數

一定数目的点或圆在等距離的排列下可以形成一个等邊三角形，這樣的數被稱為三角形數。比如10個點可以組成一个等邊三角形，因此10是一個三角形數：

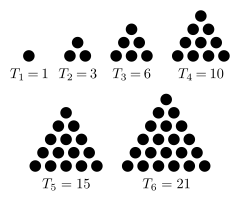
三角形數

頭30個三角形數是1, 3, 6, 10, 15, 21, 28, 36, 45, 55, 66, 78, 91, 105, 120, 136, 153, 171, 190, 210, 231, 253, 276, 300, 325, 351, 378, 406, 435, 465, ...（OEIS數列A000217）。

三角数的二倍的平方根取整，是这个三角数的序数。

性質

第n个三角形數的公式是 ${\frac {n(n+1)}{2}}$ 。
第n个三角形數是從1开始的n个自然数的和。
所有大于3的三角形數都不是质数。
除了0，1，3，21，55以外，三角形數不可能是費波那契數。
开始的n个立方数的和是第n个三角形數的平方（举例：1 + 8 + 27 + 64 = 100 = 10²）
所有三角形數的倒数之和是2。
任何三角形數乘以8再加1是一个平方数。
三角數的個位數字不可能是2、4、7、9，數字根不可能是2、4、5、7、8。
一部分三角形數（3、10、21、36、55、78……）可以用以下这个公式来表示： $n*(2n+1)$ ；而剩下的另一部分（1、6、15、28、45、66……）则可以用 $n*(2n-1)$ 来表示。
一种检验正整数x是否三角形数的方法，是计算：
$n={\frac {{\sqrt {8x+1}}-1}{2}}.$

如果n是整数，那么x就是第n个三角形数。如果n不是整数，那么x不是三角形数。这个检验法是基于恒等式 $8T_{n}+1=S_{2n+1}.$

特殊的三角形數

55、5,050、500,500、50,005,000……都是三角形數。
第11个三角形數（66）、第1111个三角形數（617,716）、第111,111个三角形數（6,172,882,716）、第11,111,111个三角形數（61,728,399,382,716）都是回文式的三角形數，但第111个、第11,111个和第1,111,111个三角形數不是。
同時為三角形數及普洛尼克數的數（不定方程 $x(x+1)={\frac {y(y+1)}{2}}$ ）：最小的幾個為0, 6, 210, 7140, 242556, 8239770,……[1][2]，對應的 $x$ 值分別為0, 2, 14, 84, 492, 2870,……（OEIS數列A053141），對應的 $y$ 值分別為0, 3, 20, 119, 696, 4059,……（OEIS數列A001652）。

它與其他數的關係

是否在相继出现的三角形数之间至少存在一个素数，在9000000以下的数目是正确的。
四面體數是三角形數在立體的推廣。
两个相继的三角形數之和是平方数。
三角平方數是同時為三角形數和平方數的數。
三角形數屬於一種多邊形數。
所有偶完美数都是三角形数。
任何自然数是最多三个三角形數的和。高斯发现了这个规律，他在1796年7月10日在日记中写道：EYPHKA! num = Δ + Δ + Δ

外部連結

Hazewinkel, Michiel (编), , , Springer, 2001, ISBN 978-1-55608-010-4
Triangular numbers（页面存档备份，存于） at cut-the-knot
There exist triangular numbers that are also square（页面存档备份，存于） at cut-the-knot
埃里克·韦斯坦因. . MathWorld.
Triangular numbers via 12 days of Christmas by Vi Hart
Hypertetrahedral Polytopic Roots by Rob Hubbard, including the generalisation to triangular cube roots, some higher dimensions, and some approximate formulae

參考資料

Sloane, N.J.A. (编). . The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
. NUMBERS APLENTY. [2021-02-05]. （原始内容存档于2021-02-25）.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] Sloane, N.J.A. (编). . The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.

[2] . NUMBERS APLENTY. [2021-02-05]. （原始内容存档于2021-02-25）.