| Chamfered square tiling | |
|---|---|
    4 colorings | |
| Symmetry | p4m, [4,4], *442 |
| Rotation symmetry | p4, [4,4]+, 442 |
| Dual | Semikis square tiling |
| Properties | |
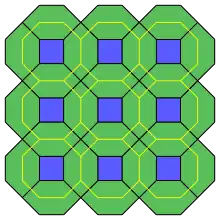
In geometry, the chamfered square tiling or semitruncated square tiling is a tiling of the Euclidean plane. It is a square tiling with each edge chamfered into new hexagonal faces.
It can also be seen as the intersection of two truncated square tilings with offset positions. And its appearance is similar to a truncated square tiling, except only half of the vertices have been truncated, leading to its descriptive name semitruncated square tiling.
Usage and Names in tiling patterns
In floor tiling, this pattern with small squares has been labeled as Metro Broadway Matte and alternate corner square tile.[1]
With large squares it has been called a Dijon tile pattern.[1]
As 3 rows of rectangles, it has been called a basketweave tiling and triple block tile pattern .[2][1]
Variations
Variations can be seen in different degrees of truncation. As well, geometric variations exist within a given symmetry. The second row shows the tilings with a 45 degree rotation which also look a little different.
Lower symmetry forms are related to the cairo pentagonal tiling with axial edges expanded into rectangles.
| *432 symmetry forms | 2*22 symmetry forms | ||||
|---|---|---|---|---|---|
| Shallow (Dijon tile) | Deep (alternate corner square tile) | Flat (Triple block) (Basketweave) | Rectangular | Concave | |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
The chiral forms be seen as two overlapping pythagorean tilings.
| Flat | Shallow | Deep | Skew | Concave |
|---|---|---|---|---|
 |
 |
 |
 |
 |
Semikis square tiling
The dual tiling looks like a square tiling with half of the squares divided into central triangles. It can be called a semikis square tiling, as alternate squares with kis operator applied. It can be seen as 4 sets of parallel lines.


