正八邊形鑲嵌
在幾何學中,正八邊形鑲嵌(英語:)是一種由正八邊形拼合,並且將正八邊形重複排列組合,並讓圖形完全拼合,而且沒有空隙或重疊的幾何構造,每個頂點皆為三個正八邊形的公共頂點,以頂點圖8.8.8或83表示。
 龐加萊圓盤模型 | |||
| 類別 | 雙曲正鑲嵌 雙曲鑲嵌 | ||
|---|---|---|---|
| 對偶多面體 | 八階三角形鑲嵌 | ||
| 識別 | |||
| 鮑爾斯縮寫 | ocat | ||
| 數學表示法 | |||
| 考克斯特符號 | |||
| 施萊夫利符號 | {8,3} t{4,8} | ||
| 威佐夫符號 | 3 | 8 2 2 8 | 4 4 4 4 | | ||
| 組成與佈局 | |||
| 面的種類 | 正八邊形 | ||
| 頂點圖 | 8.8.8 83 | ||
| 對稱性 | |||
| 對稱群 | [8,3], (*832) [8,4], (*842) [(4,4,4)], (*444) | ||
| 旋轉對稱群 | [8,3]+, (832) [8,4]+, (842) [(4,4,4)]+, (444) | ||
| 特性 | |||
| 點可遞 | |||
| 圖像 | |||
| |||
正八邊形鑲嵌是一種雙曲正鑲嵌,在施萊夫利符號中用{8,3}表示。
表面塗色
就如同平面上的正六邊形鑲嵌,正八邊形鑲嵌也具有3種不同的半正表面塗色,都可以由威佐夫結構面對稱構造出来。(h,k)表示一種表面塗色的面周期性重複,以正八邊形距離h、k計數,h在前、k在後。
| 正八邊形鑲嵌 | 截角八階正方形鑲嵌 | 大斜方截半八階正方形鑲嵌 | |
|---|---|---|---|
| 圖像 | 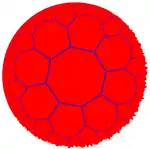 (1,0) {8,3} |
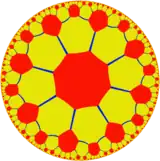 (1,1) t1,2{8,4} |
 (2,0) t0,1,2(4,4,4) |
| (h,k) 施萊夫利符號 考克斯特符號 | |||
| 對偶鑲嵌 | |||
| 圖像 | 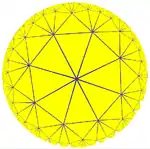 {3,8} |
 |
 f0,1,2(4,4,4) |
相關多面體及鑲嵌
| 多面体 | 欧式镶嵌 | 双曲镶嵌 | ||||||
|---|---|---|---|---|---|---|---|---|
 {2,3} |
 {3,3} |
 {4,3} |
{5,3} |
 {6,3} |
 {7,3} |
 {8,3} |
... |  {∞,3} |
 {8,2} |
 {8,3} |
 {8,4} |
 {8,5} |
 {8,6} |
 {8,7} |
 {8,8} |
... |  {8,∞} |
| 對稱群:[8,3], (*832) | [8,3]+ (832) |
[1+,8,3] (*443) |
[8,3+] (3*4) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| {8,3} | t{8,3} | r{8,3} | t{3,8} | {3,8} | rr{8,3} s2{3,8} |
tr{8,3} | sr{8,3} | h{8,3} | h2{8,3} | s{3,8} | |||
 |
 |
  |
  |
 |
 |
 |
 |
  |
  |
  | |||
| 半正對偶 | |||||||||||||
| V83 | V3.16.16 | V3.8.3.8 | V6.6.8 | V38 | V3.4.8.4 | V4.6.16 | V34.8 | V(3.4)3 | V8.6.6 | V35.4 | |||
 |
 |
 |
 |
 |
 |
 |
 |
 |
 | ||||
參考文獻
- John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 (Chapter 19, The Hyperbolic Archimedean Tessellations)
- . . Dover Publications. 1999. ISBN 0-486-40919-8. LCCN 99035678.
外部連結
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.
