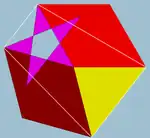
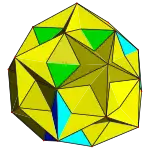
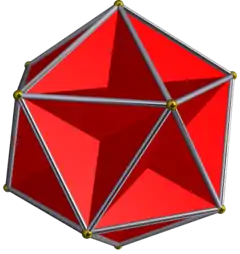
小複雜斜方截半二十面體

在幾何學中，小複雜斜方截半二十面體是一種退化的星形均勻多面體[1]，由20個正三角形、12個五角星和30個正方形組成，其可以視為大二十面體透過離面（Cantellation）或擴展（Expansion）變換而成，其外觀與小雙三斜三十二面體和五複合立方體所形成的複合幾何形狀相同[2]。

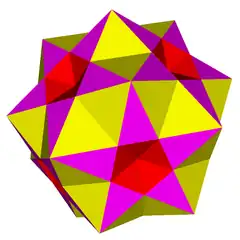小複雜斜方截半二十面體
小複雜斜方截半二十面體
類別退化均勻星形多面體
識別
名稱小複雜斜方截半二十面體
鮑爾斯縮寫
sicdatrid
數學表示法
考克斯特符號
node_1 5 rat d2 node 3 node_1 
施萊夫利符號t0,2{5/2,3}
威佐夫符號
5/2 3 | 2
性質
面62
邊120
頂點20
歐拉特徵數F=62, E=120, V=20 （χ=-38）
組成與佈局
面的種類20個正三角形
12個五角星
30個正方形
面的佈局
20{3}+12{5/2}+30{4}
頂點圖3(3.4.5/2.4)
對稱性
對稱群Ih, [5,3], *532
圖像

3(3.4.5/2.4)
（頂點圖）

性質

小複雜斜方截半二十面體是一種退化的均勻多面體，共有62個面、120條邊和20個頂點，其頂點以每三個一組為單位互相重合[2]、其邊為每兩兩一組為單位互相重合[2]。

面的組成

小複雜斜方截半二十面體由20個正三角形、12個五角星和30個正方形組成，且面在頂點周圍的分布為：每個頂點都是五角星、正方形、三角形和另外一個正方形的公共頂點，並且同時有三組相同結構，在頂點圖中可以用3[5/2,4,3,4]表示[2]，其中5/2表示五角星、4表示正方形、3表示正三角形[3]。


構成小複雜斜方截半二十面體的五角星面
構成小複雜斜方截半二十面體的正三角形面
構成小複雜斜方截半二十面體的正方形面
構成小星形截角十二面體的面在頂點周圍的排佈

相關多面體

大複雜斜方截半二十面體
大複雜斜方截半二十面體，互相相交的藍色正方形以中間透明的方式使內部的互相相交紅色五邊形可以被觀察到。

在拓樸學中，小複雜斜方截半二十面體與大複雜斜方截半二十面體拓樸同構。小複雜斜方截半二十面體可以透過將五角星面替換成五邊形面拓樸變形而得。[2][4]大複雜斜方截半二十面體的外觀與大雙三斜三十二面體和五複合立方體所形成的複合幾何形狀相同[4]。

倒角大二十面體

小複雜斜方截半二十面體可以經由大二十面體透過與正二十面體變換成小斜方截半二十面体相同的多面體變換變換而成[5]，該種變換有時稱為離面（Cantellation）或擴展（Expansion）[6]，該變換也可以視為先倒角再截角[7]，因此倒角大二十面體可以視為小複雜斜方截半二十面體截角變換的原像。倒角大二十面體與倒角大二十面體則為與五角星相鄰的面被延伸到相交形成底面為五角星的錐體替換之。


倒角大二十面體
截角的倒角大二十面體
倒角大二十面體的面
青藍色為三角形面
綠色為六邊形面
倒角大二十面體的面
在頂點周圍的排佈

複雜斜方截半大十二面體

除了大複雜斜方截半二十面體外，還有一種退化的小雙三斜三十二面體刻面多面體[8]，其為複雜斜方截半大十二面體[9]，其外觀與雙三斜十二面體和五複合立方體所形成的複合幾何形狀相同[9]。

離面（Cantellation）多面體
小複雜斜方截半二十面體
複雜斜方截半大十二面體
大複雜斜方截半二十面體
關聯多面體
大二十面體
大星形十二面體
大十二面體
小星形十二面體
正十二面體
正二十面體

參見

參考文獻
  1. Jim McNeill. . orchidpalms.com. [2019-10-05]. （原始内容存档于2019-03-11）.
  2. Klitzing, Richard. . bendwavy.org. [2019-10-05]. （原始内容存档于2016-03-25）.
  3. Coxeter, Harold Scott MacDonald; Longuet-Higgins, M. S.; Miller, J. C. P., , Philosophical Transactions of the Royal Society of London. Series A. Mathematical and Physical Sciences, 1954, 246: 401–450, ISSN 0080-4614, JSTOR 91532, MR 0062446, doi:10.1098/rsta.1954.0003
  4. Klitzing, Richard. . bendwavy.org. [2019-10-05]. （原始内容存档于2016-03-24）.
  5. Klitzing, Richard. . bendwavy.org. [2019-10-05]. （原始内容存档于2018-07-07）.
  6. Weisstein, Eric W. (编). . at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. （英语）.
  7. Deza, M. and Grishukhin, V. and Shtogrin, M. . Imperial College Press. 2004. ISBN 9781860944215. LCCN 2004445213.
  8. Klitzing, Richard. . bendwavy.org. [2019-10-05]. （原始内容存档于2016-03-24）.
  9. Klitzing, Richard. . bendwavy.org. [2019-10-05]. （原始内容存档于2016-03-25）.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.