张量代数
在数学中,一个向量空间的张量代数(),记作,是上的(任意阶)张量的代数,其乘法为张量积。张量代数左伴随于从代数到向量空间的遗忘函子,在这种意义下它是上的自由代数;在相应的泛性质的意义下,它是包含的“最一般的代数”(见下)。
张量代数也具有余代数结构。
注:本文中所有代数都假设是有单位的且结合。
构造
设是域上一个向量空间。对任何非负整数,我们定以的次张量积为与自己的次张量积:
- 。
这便是讲,由上所有秩张量组成。习惯上是基域(作为自己的一维向量空间)。
令为所有()的直和:
- 。
中的乘法由典范同构确定:
由张量积给出,然后线性扩张到所有。此乘法表明张量代数自然是一个分次代数,作为次子空间。
此构造可径直推广到任意交换环上的模上。如果是一个非交换环,我们仍然可以对任意- 双模执行这样的构造。(对通常的-模不行,因为没有迭代张量积。)
伴随与泛性质
张量代数也成为向量空间上的自由代数,并具有函子性。像其它自由构造一样,函子左伴随于某个遗忘函子,该函子将每个-代数送到它的底向量空间。
准确地说,张量代数满足如下的泛性质,正式地表明它是包含的最一般的代数:
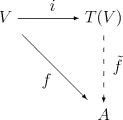
这里是到的典范包含(伴随的单位)。事实上可以定义张量代数为满足这个性质惟一的代数(确切地说,在惟一的一个同构意义下),但仍然要证明满足这个性质的对象存在。
如上泛性质说明张量代数的构造有自然的函子性。就是讲,是从-Vect,上向量空间范畴,到-Alg,-代数范畴,的一个函子。的函子性意味着任何从V到W的线性映射惟一地扩张为从到的代数同态。
非交换多项式
如果为有限维,张量代数的另一个看法是“ 上个非交换变量的多项式代数”。如果我们取的基向量,它们成为中的非交换变量(或不定元),彼此间没有任何约束(除了结合律,分配律以及K-线性)。
注意上的多项式代数不是,而是:上一个(齐次)线性函数是中的一个元素。
余代数结构
张量代数上的余代数结构如下。余积定义为
线性扩张到整个。余单位由的0-次分量。注意到保持分次:
而也与分次相容。
张量代数在这个余积下不是双代数。但下述更复杂的余积确实得到一个余代数:
这里求和取遍所有(p,m-p)-牌序。最后,对极映射为:
线性扩张到整个,这样张量代数成为一个霍普夫代数。
参见
- 对称代数
- 幺半范畴
- Stanisław Lem's Love and Tensor Algebra
参考文献
- 陈维桓. 第二版. 北京: 高等教育出版社. 2001年8月.
- Mac Lane, Saunders. Categories for the Working Mathematician(2nd ed.). GTM5. Spinger, 1998