簡單多胞形
在幾何學中,d維簡單多胞形(或稱簡單d維多胞形)是指頂點恰好只與d條稜(或d個維面)相接的d維多胞形。 d維簡單多胞形的頂點圖為(d−1)維單純形。[1]
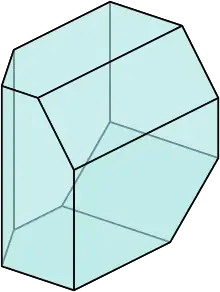
三維關聯多面體。每個頂點都恰好與三個邊、三個面相鄰,因此這是一個簡單多胞形
簡單多胞形在拓樸上的對偶是單純多胞形。同時是單純多胞形又是簡單多胞形的幾何體是單純形或二維多邊形[註 2]。 在這個定義下的三維情形是簡單多面體,這種簡單多面體[註 3]是指每個頂點指與三個面相鄰或每個頂點只與三條稜相接的多面體。這種簡單多面體的對偶多面體為「單純多面體」(即三角面多面體),其所有面都是三角形。[2]
範例
三維空間的簡單多胞形可稱為簡單多面體[註 3],其包括了稜柱(包括立方體)、正四面體和正十二面體,也有包括部分的阿基米德立體:截角四面體、截角立方体、截角八面體、大斜方截半立方体、截角十二面体、截角二十面體和大斜方截半二十面体。 一般來說,任何多面體都可以透過截去分支度為4或更高分支度的頂點來轉換成簡單多面體。 例如截對角偏方面體是截去偏方面體的高分支度頂點構成的,截對角偏方面體也是一種簡單多面體。
四維空間的簡單多胞形包括了正一百二十胞体和超立方體。簡單均勻四維多胞形包括了截角正五胞体、截角超立方體、截角正二十四胞体、截角正一百二十胞体、柱體柱。此外,所有的過截角四維多胞體都是簡單多胞形。
更高維度的簡單多胞形包括了d維單純形、超方形、關聯多面體和排列多面體。
唯一建構
米夏·佩爾斯推測簡單多胞形完全由其一階骨架(1-skeleton)所決定。[3]他的猜想於 1987年被羅斯威莎·布林德和彼得·馬尼·萊維茨卡(Peter Mani-Levitska)證明。後來吉爾卡萊基於唯一沉向理論對此結論提供了更簡潔的證明。[4]
參見
- 單純多胞形
註釋
參考文獻
- Ziegler, Günter M., , Graduate Texts in Mathematics 152, Springer: 8, 2012, ISBN 9780387943657
- Cromwell, Peter R., , Cambridge University Press: 341, 1997, ISBN 0-521-66405-5
- Blind, Roswitha; Mani-Levitska, Peter, , Aequationes Mathematicae, 1987, 34 (2-3): 287–297, MR 0921106, doi:10.1007/BF01830678
- Kalai, Gil, , Journal of Combinatorial Theory, Series A, 1988, 49 (2): 381–383, MR 0964396, doi:10.1016/0097-3165(88)90064-7
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.