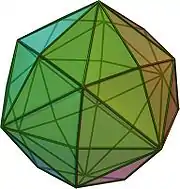
大斜方截半立方体
在幾何學中,大斜方截半立方體,又稱為截角截半立方體,是一種阿基米德立體。這個多面體共由26個面、72條邊和48個頂點所組成,其中,26個面中包含了 12個正方形面、8個正六邊形面以及6個正八邊形面。由於每個面都存在點對稱性質,因此大斜方截半立方體也是一種環帶多面體。
 (點選觀看旋轉模型) | |||||
| 類別 | 半正多面體 | ||||
|---|---|---|---|---|---|
| 對偶多面體 | 四角化菱形十二面體 | ||||
| 識別 | |||||
| 名稱 | 大斜方截半立方體 | ||||
| 參考索引 | U11, C23, W15 | ||||
| 鮑爾斯縮寫 | girco | ||||
| 數學表示法 | |||||
| 考克斯特符號 | |||||
| 施萊夫利符號 | tr{4,3} | ||||
| 威佐夫符號 | 2 3 4 | | ||||
| 康威表示法 | bC taC | ||||
| 性質 | |||||
| 面 | 26 | ||||
| 邊 | 72 | ||||
| 頂點 | 48 | ||||
| 歐拉特徵數 | F=26, E=72, V=48 (χ=2) | ||||
| 組成與佈局 | |||||
| 面的種類 | 正方形 正六邊形 正八邊形 | ||||
| 面的佈局 | 12{4}+8{6}+6{8} | ||||
| 頂點圖 | 4.6.8 | ||||
| 對稱性 | |||||
| 對稱群 | Oh群 | ||||
| 特性 | |||||
| 環帶多面體 | |||||
| 圖像 | |||||
| |||||
其他名稱
這個立體有多種名稱:
- 大斜方截半立方體(英語:[註 1]),由羅伯特·威廉斯命名[1]
- 截角截半立方體(英語:),由約翰尼斯·克卜勒命名[2]
- 斜方截角立方體(英語:),由馬格努斯·文寧格命名[3]
- 大斜方截半立方體(英語:[註 1]),由皮特·克倫威爾命名[4]
- 全截立方體(英語:),由諾曼·約翰遜命名
名稱截角截半立方體(英語:)最初是約翰尼斯·克卜勒命的名稱,但這個名稱有點會引起誤解,因為若將截半立方體進行截角操作的話,即切去截半立方體的所有頂點之後,得到的立體圖形將不會是均勻的形狀,會出現長方形的面,但由於他們可以藉由變形變成半正多面體大斜方截半立方體,因此他們在拓樸學上是一樣的[5]。
性質
大斜方截半立方體是一種阿基米德立體,由於每一個面都是正多邊形,因此也符合托羅爾德戈塞特在1900為給出的半正多面體定義[6][7]。此外,大斜方截半立方體也是一種環帶多面體,並屬於八面體對稱。
面的組成
大斜方截半立方體是一種半正多面體,換言之即其面皆由正多邊形組成。大斜方截半立方體具有26個面,因此也可以稱為半正二十六面體,但半正二十六面體不只一種,小斜方截半立方体也是一個具有26個面的半正多面體。組成大斜方截半立方體的26個面中,其中12個面是正方形面、8個面是正六邊形面以及另外6個正八邊形的面。
作法
構成大斜方截半立方體有多種方法,其中一種是將立方體(或正八面體)的十二條棱切一刀,並且在八個(正八面體為六個)頂點處切一刀,但是要切的薄一點,切的深度與截半相當,就可以得到一個大斜方截半立方體。
拆解
| 虧格 3 | 虧格 5 | 虧格 7 | 虧格 11 |
|---|---|---|---|
 |
 |
 |
 |
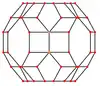
正交投影
| 建立於 | 頂點 | 四邊形-六邊形 交棱 |
四邊形-八邊形 交棱 |
四邊形-八邊形 交棱 |
四邊形-六邊形 交面 |
|---|---|---|---|---|---|
| 圖像 |  |
 |
 |
 |
 |
| 投影對稱性 | [2]+ | [2] | [2] | [2] | [2] |
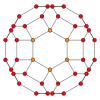
| 建立於 | 正方形面 | 正八邊形面 | 正方形面 | 正六邊形面 | 正八邊形面 |
| 圖像 |  |
 |
 |
 |
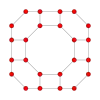 |
| 投影對稱性 | [2] | [2] | [2] | [6] | [8] |
相關多面體及鑲嵌
| 對稱性: [4,3], (*432) | [4,3]+ (432) |
[1+,4,3] = [3,3] (*332) |
[3+,4] (3*2) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| {4,3} | t{4,3} | r{4,3} r{31,1} |
t{3,4} t{31,1} |
{3,4} {31,1} |
rr{4,3} s2{3,4} |
tr{4,3} | c{4,3} | sr{4,3} | h{4,3} {3,3} |
h2{4,3} t{3,3} |
s{3,4} s{31,1} |
= |
= |
= |
|||||||||
| 對偶多面體 | |||||||||||
| V43 | V3.82 | V(3.4)2 | V4.62 | V34 | V3.43 | V4.6.8 | V4.62/63 | V34.4 | V33 | V3.62 | V35 |
參見
註釋
- Great rhombcuboctahedron(大斜方截半立方體)這一名稱和Great rhombicuboctahedron(大斜方截半立方體)差異在前者的rhombcuboctahedron比後者的rhombicuboctahedron少一個「i」字母
參考文獻
- Williams, Robert. . Dover Publications, Inc. 1979. ISBN 0-486-23729-X. (Section 3-9, p. 82)
- Ball, W. W. R. and Coxeter, H. S. M. Mathematical Recreations and Essays, 13th ed. (页面存档备份,存于) New York: Dover, p. 138, 1987.
- Wenninger, Magnus, , Cambridge University Press, 1974, ISBN 978-0-521-09859-5, MR 0467493 (Model 15, p. 29)
- Cromwell, P.; Polyhedra, CUP hbk (1997), pbk. (1999). (p. 82)
- Cundy, H. and Rollett, A. "Great Rhombicuboctahedron or Truncated Cuboctahedron. 4.6 .8." §3.7.6 in Mathematical Models, 3rd ed. Stradbroke, England: Tarquin Pub., p. 106, 1989.
- Thorold Gosset On the Regular and Semi-Regular Figures in Space of n Dimensions, Messenger of Mathematics, Macmillan, 1900
- Coxeter, H.S.M. Regular polytopes, 3rd Edn, Dover (1973)
- Read, R. C.; Wilson, R. J., , Oxford University Press: 269, 1998
- Cromwell, P. . United Kingdom: Cambridge. 1997: 79–86 Archimedean solids. ISBN 0-521-55432-2.
外部連結
- 埃里克·韦斯坦因, 大斜方截半立方体 (參閱阿基米德立體) 於MathWorld(英文)
- Klitzing, Richard. . bendwavy.org.
- Editable printable net of a truncated cuboctahedron with interactive 3D view(页面存档备份,存于)
- The Uniform Polyhedra(页面存档备份,存于)
- Virtual Reality Polyhedra(页面存档备份,存于) The Encyclopedia of Polyhedra
- great Rhombicuboctahedron: paper strips for plaiting(页面存档备份,存于)
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.