立方半八面體
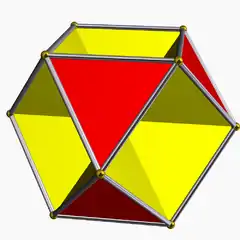
在幾何學中,立方半八面體是一種非凸多面體,屬於星形多面體及均勻多面體,也可以歸類在非凸均勻多面體,其索引在均勻多面中是U15[1]、溫尼爾多面體模型中是W78[2]。立方半八面體外觀看起來像所有三角形面都凹進去的截半立方體。[3]:78立方半八面體由6個正方形和4個正六邊形組成,是一種十面體,且每個頂點對應的角皆相等,因此也可以被歸類為擬正多面體[4],然而由於這個立體同時具備半多面體的特性,因此被部分學者分成一類新的立體,即擬正半多面體(Versi-Regular Polyhedra),這類立體共有九個,最早在1881年由亞伯特·巴杜羅()發現並描述[5]。
 | ||||
| 類別 | 均勻星形多面體 | |||
|---|---|---|---|---|
| 對偶多面體 | 立方半無窮星形八面體 | |||
| 識別 | ||||
| 名稱 | 立方半八面體 | |||
| 參考索引 | U15, C51, W78 | |||
| 鮑爾斯縮寫 | cho | |||
| 數學表示法 | ||||
| 考克斯特符號 | ||||
| 威佐夫符號 | 4/3 4 | 3 (二重覆蓋) | |||
| 性質 | ||||
| 面 | 10 | |||
| 邊 | 24 | |||
| 頂點 | 12 | |||
| 歐拉特徵數 | F=10, E=24, V=12 (χ=-2) | |||
| 組成與佈局 | ||||
| 面的種類 | 6個四邊形{4} 4個六邊形{6} | |||
| 面的佈局 | 6{4}+4{6} | |||
| 頂點圖 | 4.6.4/3.6 | |||
| 對稱性 | ||||
| 對稱群 | Oh, [4,3], *432 | |||
| 特性 | ||||
| 均勻 | ||||
| 圖像 | ||||
| ||||
性質
立方半八面體共有10個面、24條邊和12個頂點[6][7]。在其10個面中有6個正方形面和4個六邊形面。這6個正方形面的排列方式與截半立方體的六個正方形面相同[8]:108 。立方半八面體每個頂點都是2個正方形和2個六邊形的公共頂點。其中,有一個四邊形反向相接,使得其頂點圖為交叉四邊形,在頂點布局中,可以用4.6.4/3.6來描述。[9][6]
相關多面體
立方半八面體與截半立方體和八面半八面體有著相同的頂點布局與稜布局。[14]
 截半立方體 |
 立方半八面體 |
 八面半八面體 |
立方半無窮星形八面體
 | |
| 類別 | 無窮星形多面體 半多面體對偶 |
|---|---|
| 對偶多面體 | 立方半八面體 |
| 識別 | |
| 名稱 | 立方半無窮星形八面體 |
| 參考索引 | DU15 |
| 性質 | |
| 面 | 12 |
| 邊 | 24 |
| 頂點 | 10 |
| 歐拉特徵數 | F=12, E=24, V=10 (χ=-2) |
| 對稱性 | |
| 對稱群 | Oh, [4,3], *432 |
立方半無窮星形八面體是立方半八面體的對偶多面體,也是九個對偶半多面體之一[16]。其外觀難以與八面半無窮星形八面體區別。[17]
| 多面體 |  立方半八面體 |
 八面半八面體 |
|---|---|---|
| 對偶多面體 |  立方半無窮星形八面體 |
 八面半無窮星形八面體 |
從定義上來看,對偶多面體的面會與原始立體的頂點圖相同,同時頂點周圍之面的排列方式會和原始立體的面之邊相同,也就是說對偶多面體的頂點圖為原始立體的面[18]。由於立方半無窮星形八面體是立方半八面體的對偶多面體,而立方半八面體的12個頂點皆為4個面的公共頂點,因此立方半無窮星形八面體的面理應具有12個面,每個面由4個邊組成[19]。然而立方半八面體有部分面幾何中心落在整個立體的幾何中心上,因此其對偶多面體的頂點會落在無窮遠處,即無窮实射影平面上的點。[20]一般來說,這樣的立體無法被具象化[19]。為了具像化這種立體,溫尼爾在著作《對偶模型》中將其描述為由無限高的柱體組合構成的立體,在這樣的視覺化方式下,立方半八面體外觀為由4個無限高的六角柱構成的立體[20]。然而這樣的具象化結果會使得其外觀與八面半無窮星形八面體的具象化結果相同。[21]
參見
註釋
參考文獻
- . 密西根州立大學圖書館. [2016-08-31]. (原始内容存档于2013-06-20).
- . colinspics. [2016-08-31]. (原始内容存档于2016-08-31).
- Wenninger, M.J. . Cambridge University Press. 1974 [2021-09-06]. ISBN 9780521098595. LCCN 69010200. (原始内容存档于2021-08-31).
- George W. Hart. . 1996 [2021-09-05]. (原始内容存档于2021-08-30).
- Jean Paul Albert Badoureau. . Journal de l'École polytechnique. 1881, (49): 47-172.
- . mathconsult. [2016-08-31]. (原始内容存档于2016-03-27).
- . bulatov.org. [2016-08-31]. (原始内容存档于2016-04-01).
- Pisanski, T. and Servatius, B. . Birkhäuser Advanced Texts Basler Lehrbücher. Birkhäuser Boston. 2012 [2021-09-06]. ISBN 9780817683634. LCCN 2012944998. (原始内容存档于2021-09-06).
- Robert Webb. . software3d.com. [2021-09-06]. (原始内容存档于2020-03-29).
- . Regular Map database - map details. [2021-07-24]. (原始内容存档于2021-08-02).
- Barnes, J. . SpringerLink: Bücher. Springer Berlin Heidelberg. 2012 [2021-09-06]. ISBN 9783642309649. LCCN 2012946175. (原始内容存档于2021-09-06).
- . dmccooey.com. [2016-08-31]. (原始内容存档于2016-03-24).
- Jean Paul Albert Badoureau, Mémoire sur les Figures Isocèles, Journal de l'École polytechnique 49 (1881), 47-172.
- Klitzing, Richard. . bendwavy.org. [2021-09-06]. (原始内容存档于2021-01-23).
- David I. McCooey. . dmccooey.com. [2021-09-05]. (原始内容存档于2021-07-30).
- Magnus Wenninger, , Cambridge University Press, 1983, ISBN 978-0-521-54325-5, MR 0730208 (Page 101, Duals of the (nine) hemipolyhedra)
- Weisstein, Eric W. (编). . at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. (英语).
- Weisstein, Eric W. (编). . at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. (英语).
- Vladimir Bulatov. . Polyhedra Collection, bulatov.org. [2021-07-30]. (原始内容存档于2020-02-23).
- Wenninger, Magnus, , Cambridge University Press, 2003 [1983], ISBN 978-0-521-54325-5, MR 0730208, doi:10.1017/CBO9780511569371 (Page 101, Duals of the (nine) hemipolyhedra)
- Weisstein, Eric W. (编). . at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. (英语).
- Guy's polyhedra pages. . steelpillow. 2006年7月11日 [2019年5月31日]. (原始内容存档于2016年3月13日).




