Delta位勢阱

一個粒子獨立於時間的薛丁格方程為

${\displaystyle -{\frac {\hbar ^{2}}{2m}}{\frac {d^{2}\psi (x)}{dx^{2}}}+V(x)\psi (x)=E\psi (x)\,\!}$；

其中，${\displaystyle \hbar \,\!}$是約化普朗克常數，${\displaystyle m\,\!}$是粒子質量，${\displaystyle x\,\!}$是粒子位置，${\displaystyle E\,\!}$是能量，${\displaystyle \psi (x)\,\!}$是波函數，${\displaystyle V(x)\,\!}$是位勢，表達為

${\displaystyle V(x)=-\lambda \delta (x)\,\!}$；

其中，${\displaystyle \delta (x)\,\!}$是狄拉克Delta函數，${\displaystyle \lambda \,\!}$是狄拉克Delta函數的強度。

這位勢阱將一維空間分為兩個區域：${\displaystyle x<0\,\!}$與${\displaystyle x>0\,\!}$。在任何一個區域內，位勢為常數，薛丁格方程的解答可以寫為往右與往左傳播的波函數的的疊加（參閱自由粒子）：

${\displaystyle \psi _{L}(x)=A_{r}e^{ikx}+A_{l}e^{-ikx}\quad x<0\,\!}$，

${\displaystyle \psi _{R}(x)=B_{r}e^{ikx}+B_{l}e^{-ikx}\quad x>0\,\!}$；

其中，${\displaystyle A_{r}\,\!}$、${\displaystyle A_{l}\,\!}$、${\displaystyle B_{r}\,\!}$、${\displaystyle B_{l}\,\!}$都是必須由邊界條件決定的常數，下標${\displaystyle r\,\!}$與${\displaystyle l\,\!}$分別標記波函數往右或往左的方向。${\displaystyle k={\sqrt {2mE/\hbar ^{2}}}\,\!}$是波數。

當${\displaystyle E>0\,\!}$時，${\displaystyle \psi _{L}\,\!}$與${\displaystyle \psi _{R}\,\!}$都是行進波。可是，當${\displaystyle E<0\,\!}$時，${\displaystyle \psi _{L}\,\!}$與${\displaystyle \psi _{R}\,\!}$都隨著座標${\displaystyle x\,\!}$呈指數遞減或指數遞增。

在${\displaystyle x=0\,\!}$处，邊界條件是：

${\displaystyle \psi _{L}=\psi _{R}\,\!}$，

${\displaystyle {\frac {d}{dx}}\psi _{L}={\frac {d}{dx}}\psi _{R}-{\frac {2m\lambda }{\hbar ^{2}}}\psi _{R}\,\!}$。

特別注意第二個邊界條件方程式，波函數隨位置的導數在${\displaystyle x=0\,\!}$並不是連續的，在位勢阱兩邊的差額有${\displaystyle {\frac {2\lambda }{\hbar ^{2}}}\psi _{R}\,\!}$這麼多。這方程式的推導必須用到薛丁格方程。將薛丁格方程積分於${\displaystyle x=0\,\!}$的一個非常小的鄰域：

${\displaystyle -{\frac {\hbar ^{2}}{2m}}\int _{-\epsilon }^{\epsilon }{\frac {d^{2}\psi }{dx^{2}}}\,dx+\int _{-\epsilon }^{\epsilon }V(x)\psi \,dx=E\int _{-\epsilon }^{\epsilon }\psi \,dx\,\!}$；(1)

其中，${\displaystyle \epsilon \,\!}$是一個非常小的數值。

方程式(1)右邊的能量項目是

${\displaystyle E\int _{-\epsilon }^{\epsilon }\psi \,dx\approx E\cdot 2\epsilon \cdot \psi (0)\,\!}$。(2)

当${\displaystyle \epsilon \to 0\,\!}$时，该項趋向于0。

方程式(1)左邊是

${\displaystyle -{\frac {\hbar ^{2}}{2m}}\left({\frac {d\psi _{R}}{dx}}{\bigg |}_{\epsilon }-{\frac {d\psi _{L}}{dx}}{\bigg |}_{-\epsilon }\right)+\lambda \int _{-\epsilon }^{\epsilon }\delta (x)\psi \,dx=0\,\!}$(3)

根據狄拉克Delta函數的定義，

${\displaystyle \int _{-\epsilon }^{\epsilon }\delta (x)\psi \,dx=\psi _{R}(0)\,\!}$。(4)

而在${\displaystyle \epsilon \to 0\,\!}$的極限，

${\displaystyle \lim _{\epsilon \to 0}{\frac {d\psi _{L}}{dx}}{\bigg |}_{-\epsilon }={\frac {d\psi _{L}}{dx}}{\bigg |}_{0}\,\!}$，(5)

${\displaystyle \lim _{\epsilon \to 0}{\frac {d\psi _{R}}{dx}}{\bigg |}_{\epsilon }={\frac {d\psi _{R}}{dx}}{\bigg |}_{0}\,\!}$。(6)

將這些結果(4)，(5)，(6)代入方程式(3)，整理后，可以得到第二個邊界條件方程式：在${\displaystyle x=0\,\!}$，

${\displaystyle {\frac {d\psi _{L}}{dx}}={\frac {d\psi _{R}}{dx}}-{\frac {2m\lambda }{\hbar ^{2}}}\psi _{R}\,\!}$。

從這兩個邊界條件方程式。稍加運算，可以得到以下方程式：

${\displaystyle A_{r}+A_{l}=B_{r}+B_{l}\,\!}$，

${\displaystyle ik(A_{r}-A_{l}-B_{r}+B_{l})={\frac {2m\lambda }{\hbar ^{2}}}(B_{r}+B_{l})\,\!}$。

散射態

一個Delta位勢阱的反射係數${\displaystyle R\,\!}$（用紅線表示）與透射係數${\displaystyle T\,\!}$（用綠線表示）隨著能量${\displaystyle E\,\!}$的變化。在這裏，能量${\displaystyle E>0\,\!}$。能量的單位是${\displaystyle {\frac {\lambda ^{2}}{2m\hbar ^{2}}}\,\!}$。經典力學的答案用虛線表示，量子力學的答案用實線表示。

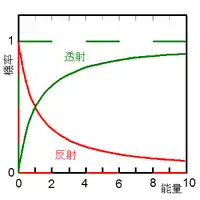
假若，能量是正值的，粒子可以自由的移動於位勢阱外的兩個半空間，${\displaystyle x<0\,\!}$或${\displaystyle x>0\,\!}$。在這裏，粒子的量子行為主要是由Delta位勢阱造成的散射行為。稱這粒子的量子態為散射態。設定粒子從左邊入射。在Delta位勢阱，粒子可能會被反射回去，或者會被透射過去。我們想要知道散射的反射係數與透射係數。設定${\displaystyle A_{r}=1\,\!}$，${\displaystyle A_{l}=r\,\!}$，${\displaystyle B_{l}=0\,\!}$，${\displaystyle B_{r}=t\,\!}$。求算反射的機率幅${\displaystyle r\,\!}$與透射的機率幅${\displaystyle t\,\!}$：

${\displaystyle r=-\ {\cfrac {1}{{\cfrac {i\hbar ^{2}k}{m\lambda }}+1}}\,\!}$，

${\displaystyle t={\cfrac {1}{-\ {\cfrac {im\lambda }{\hbar ^{2}k}}+1}}\,\!}$。

反射係數是

${\displaystyle R=|r|^{2}={\cfrac {1}{1+{\cfrac {\hbar ^{4}k^{2}}{m^{2}\lambda ^{2}}}}}={\cfrac {1}{1+{\cfrac {2\hbar ^{2}E}{m\lambda ^{2}}}}}\,\!}$。

這純粹是一個量子力學的效應；在經典力學裏，這是不可能發生的。

透射係數是

${\displaystyle T=|t|^{2}=1-R={\cfrac {1}{1+{\cfrac {m^{2}\lambda ^{2}}{\hbar ^{4}k^{2}}}}}={\cfrac {1}{1+{\cfrac {m\lambda ^{2}}{2\hbar ^{2}E}}}}\,\!}$。

• 由於模型的對稱性，假若，粒子從右邊入射，我們也會得到同樣的答案。
• 很奇異地，給予同樣的能量、質量、與狄拉克Delta函數的強度，Delta位勢壘與Delta位勢阱有同樣的反射係數與透射係數。

束縛態

Delta位勢阱的束縛態，在任何一個位置，波函數都是連續的；可是，除了在${\displaystyle x=0\,\!}$以外，在其它任何位置，波函數隨位置的導數都是連續的。

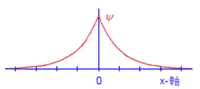
每一個一維的吸引位勢，都至少會存在著一個束縛態（）。由於${\displaystyle E<0\,\!}$，波數變為複數。設定${\displaystyle \kappa =-ik={\sqrt {2m|E|/\hbar ^{2}}}\,\!}$。前述的振盪的波函數${\displaystyle \psi _{L}\,\!}$與${\displaystyle \psi _{R}\,\!}$，現在卻隨著座標${\displaystyle x\,\!}$呈指數遞減或指數遞增。為了要符合物理的真實性，我們要求波函數不發散於${\displaystyle x\to \pm \infty \,\!}$。那麼，${\displaystyle A_{r}\,\!}$與${\displaystyle B_{l}\,\!}$必須被設定為0。波函數變為

${\displaystyle \psi _{L}(x)=A_{l}e^{\kappa x}\,\!}$，

${\displaystyle \psi _{R}(x)=B_{r}e^{-\kappa x}\,\!}$。

從邊界條件與歸一條件，可以得到

${\displaystyle A_{l}=B_{r}={\sqrt {\kappa }}\,\!}$，

${\displaystyle \kappa ={\frac {m\lambda }{\hbar ^{2}}}\,\!}$。

Delta位勢阱只能有一個束縛態。束縛態的能量是

${\displaystyle E=-\ {\frac {\hbar ^{2}\kappa ^{2}}{2m}}=-\ {\frac {m\lambda ^{2}}{2\hbar ^{2}}}\,\!}$。

束縛態的波函數是

${\displaystyle \psi (x)={\frac {\sqrt {m\lambda }}{\hbar }}e^{-m\lambda \mid x\mid /\hbar ^{2}}\,\!}$。

Delta位勢阱是有限深方形阱的一個特別案例。在有限深位勢阱的深度${\displaystyle V_{0}\to \infty \,\!}$與阱寬${\displaystyle L\to 0\,\!}$的極限，同時保持${\displaystyle V_{0}L=\lambda \,\!}$，就可以從有限深位勢阱的波函數，得到Delta位勢阱的波函數。

当核间距R=2时，双势井狄拉克Delta函数模型中的对称与反对称的波函数

Delta函數模型其實是氫原子的一維版本根據維度比例由 达德利·赫施巴赫（“Dudley R. Herschbach”）[1]團隊所研發。此 delta函數模型以雙井迪拉克Delta函數模型最有用，因其代表一維版的水分子離子。

雙井迪拉克Delta函數模型是用以下薛丁格方程描述：

${\displaystyle -{\frac {\hbar ^{2}}{2m}}{\frac {d^{2}\psi }{dx^{2}}}(x)+V(x)\psi (x)=E\psi (x)}$

電位現為：

${\displaystyle V(x)=-q\left[\delta (x-{\frac {R}{2}})+\lambda \delta (x+{\frac {R}{2}})\right]}$

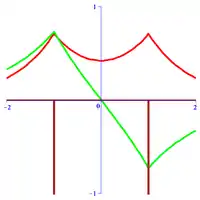
其中${\displaystyle 0<R<\infty }$是「核間」距離於迪拉克Delta函數（負）峰值位於${\displaystyle x=\pm {\textstyle {\frac {R}{2}}}}$（圖表中棕色所示）。記得此模型與其三維分子版本的關係，我們用原子单位制且設${\displaystyle \hbar =m=1}$。此處${\displaystyle 0<\lambda <1}$為一可調參數。從單井的例子，可推論擬設於此解為：

${\displaystyle \psi (x)~=~Ae^{-d\left|x-{\frac {R}{2}}\right|}+Be^{-d\left|x+{\frac {R}{2}}\right|}}$

令波函數於Delta函數峰值相等可得行列式：

${\displaystyle \left|{\begin{array}{cc}q-d&qe^{-dR}\\q\lambda e^{-dR}&q\lambda -d\end{array}}\right|=0~,\qquad E=-{\frac {d^{2}}{2}}~.}$

因此，${\displaystyle d}$是由偽二次式方程：

${\displaystyle d_{\pm }(\lambda )~=~{\textstyle {\frac {1}{2}}}q(\lambda +1)\pm {\textstyle {\frac {1}{2}}}\left\{q^{2}(1+\lambda )^{2}-4\,\lambda q^{2}\lbrack 1-e^{-2d_{\pm }(\lambda )R}]\right\}^{1/2}}$

它有兩解${\displaystyle d=d_{\pm }}$。若等價情況（對稱單核），${\displaystyle \lambda =1}$則偽二次式化為：

${\displaystyle d_{\pm }=q[1\pm e^{-d_{\pm }R}]}$

此「+」代表了對稱於中點的波函數（圖中紅色）而${\displaystyle A=B}$稱為偶態。接著，「-」情況為反對稱於中點的波函數其${\displaystyle A=-B}$稱為非偶態（圖中綠色）。它們代表著三維${\displaystyle H_{2}^{+}}$的兩種最低能態之近似且有助於其分析。對稱電價的特徵能分析解為[2]：

${\displaystyle d_{\pm }=q~+~W(\pm qRe^{-qR})/R}$

其中W是標準朗伯W函数注意此最低能對應於對稱解${\displaystyle d_{+}}$。當非等電價，此為三維分子問題，其解為一般化Lambert W函數（見一般化朗伯W函数章節與相關參考）。

1. D.R Herschbach, J.S. Avery, and O. Goscinski (eds.), Dimensional Scaling in Chemical Physics, Springer, (1992). （页面存档备份，存于）
2. T.C. Scott, J.F. Babb, Alexander Dalgarno and John D. Morgan III, "The Calculation of Exchange Forces: General Results and Specific Models", J. Chem. Phys., 99, pp. 2841-2854, (1993).

• 自由粒子
• 無限深方形阱
• 有限深方形阱
• 有限位勢壘
• 球對稱位勢
• Delta位勢壘
• 量子穿隧效應