X
这篇文章由我们训练有素的编辑和研究团队共同创作,他们对文章的准确性和全面性进行了验证。
wikiHow的内容管理团队会严密监督编辑人员的工作,确保每篇文章都符合我们的高质量标准要求。
这篇文章已经被读过31,444次。
“加法”是少数几项我们从学校中学会的很有实践运用意义的技能。所幸,学习加法一点也不难。并且,针对数字的不同,可以采取不同的技巧,从而方便加法的运算,而这些技巧都可以从wikiHow中找到。下面就先从本文的方法开始学起吧。
步骤
方法 1
方法 1 的 5:
小数字相加运算
-
首先熟悉加法的概念。拿出一把小黄豆(或其它小物体)。将一些黄豆放在一边形成一堆,然后从1开始数这一堆黄豆有多少个(从1、2、3数到最后一个黄豆)。数到最后一个黄豆的数字就是这一堆黄豆的总数。在纸上记录黄豆总数的数字。然后再数另一堆有多少个黄豆。此时,将两堆黄豆放在一起。这一大堆黄豆有多少个呢?你可以再从1开始数豆子。最后就会发现混合后豆子的总数就是之前两堆豆子的数量相加的和。这就是加法运算。
- 例如,第一堆有5个豆子,第二堆有3个豆子。当你将两堆豆子混在一起再进行计数时,发现总共有8个豆子。这就是5 + 3等于8。
-
学习“数对”。由于大多数人都习惯以10为单位计数,所以熟记和为10的一对数可以让加法更简单。掌握那些两数和为10的数对。例如:1+9,2+8,3+7,4+6,5+5。
-
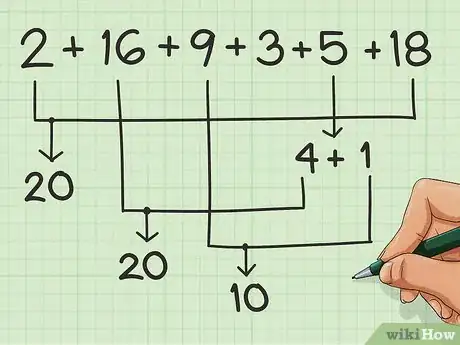
尽可能地将数字配对组成“数对”。尽可能地将数字和数字配对,使之和为十的倍数。
- 让我们以下列数字为例:2,16,9,3,5,18。你可以将2和18配对相加得到20。由于4和6相加正好是10,那么从5取出4来和16相加得到20,。然后将剩余的1和9相加得到10。
-
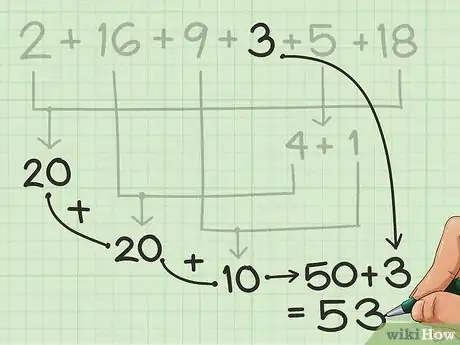
将额外部分数字相加。凑完整十数之后,再加上余下的数字,用笔算或心算将其相加即可。
- 在之前的例子中,将数对相加后得到50,只剩下3这个数字。这就非常简单了。你可以在脑海中进行简单的计算,将50和3相加即可得到结果。
-
仔细检查你的运算结果。只要有时间,你最好每次都用其它方法来复检你的运算结果以保证运算正确。广告
方法 2
方法 2 的 5:
大数目相加运算
-
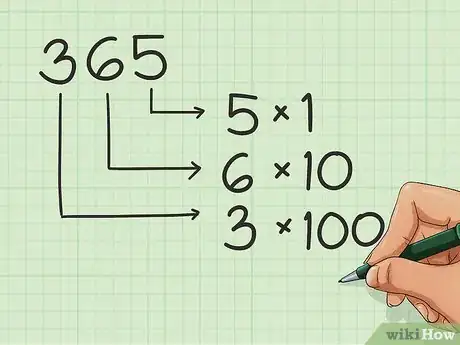
学习数位的概念。当你书写数字时,每个数字的位置都有其特定的名字或类型。掌握数位的概念可以帮助你正确地排列数字及运算。例如:
- 在2中,数字2本身位于个位数位置。
- 在数字20中,2位于十位数的位置。
- 在数字200中,2位于百位数的位置。
- 所以,在数字365中,5位于个位数位置,6位于十位数位置,3位于百位数位置。
-
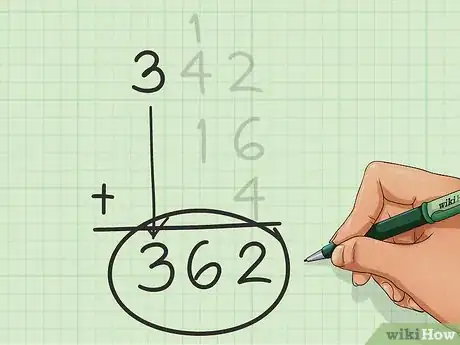
排列数字。在计算加法运算时,先将数字按位数从多到少来从上向下地排列数字。排列数字是为了让数字的每个相同的数位进行对齐。如果一个数字没有高位数,那么就在其左侧空出一个数位。例如,如果你想要计算16、4和342相加的结果,你应该这样写下三个数字:
- 342
- _16
- __4
-
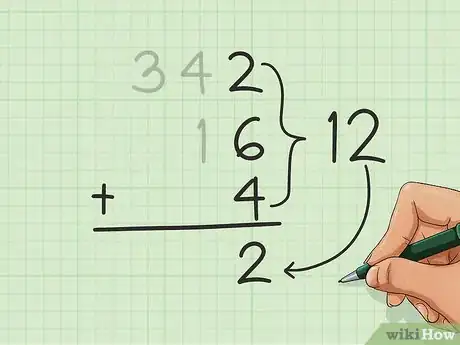
将第一列数字相加。从右边开始,将最右侧的一列数字相加。将相加得到的结果写在这一列的下方位置。按照该法将其它列数字相加并写下结果。
- 在我们上面的例子中。当我们将右侧的2、6和4相加时,得到12。然后将12中的2写在最右栏的下方。
-
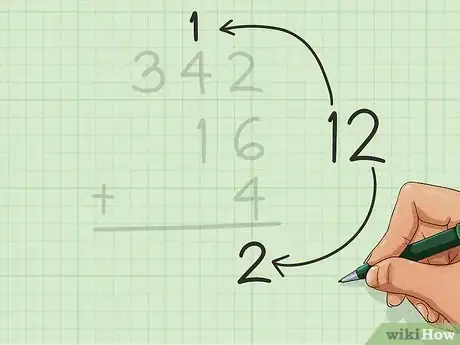
向前一个数位进位。如果个位数数字相加得到的结果在十位数上有数字,那么在左侧一栏的顶部写下十位上的数字。
- 在本例中,个位数相加得到12,我们将其中的1写在中间一栏的顶部。即342中4的上方。
-
计算下一栏。计算完个位数一栏,我们需要计算左侧十位上数字之和,这也包括进位的数字。然后将计算结果写在中间栏的下方。
- 在本例中,我们将12中的1、342中的4和16中的1相加得到6。
-
得到最后的和。从右向左,按上述方法将每一栏的数字相加,直到所有位数计算完毕。那么写在底部的数字就是加法运算的结果。
- 在本例中,三数之和是362。
广告
方法 3
方法 3 的 5:
小数的加法运算
-
将小数进行排列。当一个数字带有小数点时(例如:24.5),那么你在计算小数相加时要格外仔细才行。主要的窍门就是根据小数点的位置排列所有数字。数字的小数点对齐,自成一列。[1] 例如:
- 107.8
- _24.5
- __3.2
- _15.0
-
排列没有小数点的数字。如果其中一个加数没有小数点,那么在其右侧补一位小数点后的0来对齐数字。
- 在上述例子中,由于15后面没有0,所以在15后加一个小数点和0,使得数字的列一目了然。
-
按照正常的计算规则来相加。当你将数字正确地排列起来后,你就将每个数位上数字相加来求和即可。
- 本例的和为150.5。
广告
方法 4
方法 4 的 5:
分数的加法运算
-
将各个分数的分母化为相同的分母。分母是分数式横线下方的数字。在计算分数相加时,你需要将分母化成相同的数字,然后将分子相加。你可以将分子分母同时乘以(或除以)一个相同的数字来转化分数,知道所有分数的分母大小相同。例如,我们想要计算1/8和3/4的和:
- 首先需要将两者的分母化成一样的。那么如何将4化成8呢?方法就是将分子分母同时乘以2!
- 将分数3/4的3和4都乘以2得到6/8。
-
将分子相加。分子是分数式横线上方的数字。现在我们有分数1/8和6/8,我们将1和6相加得到7。
-
得到和。将分子相加的和放在分母的上方,分母保持不变,得到最终的结果。在本例中,最后的结果是7/8。
-
化简分数。你也许希望简化分数来方便阅读。你可以用分子和分母同时除以其相同的因数来化简分数。在本例中,我们不需要化简。因为它已经是最简形式了。但是如果你得到的是一个像3/6这样的结果,那么你需要将其进行化简。
- 当我们发现分子分母可以同时除以一个小数字时,我们就可以将分数化简。在本例中,我们用两者都除以3来化简,得到结果1/2。
广告
方法 5
方法 5 的 5:
加法技巧
-
凑数计算。如果你只计算几个数字的和,并且这些数字中没有恰巧可以凑成整10数的,那么你可以通过加上或者减去一个数来简化计算。比如, 19 + 30,相比之下20 + 30是不是更好计算呢? 所以,先给19加1,然后再计算结果,最后再从结果中减去1,即:19 + 1 + 30 = 50,50 - 1 = 49。
-
分组。和上面讨论的“数对”类似,将所有的数字分组,让每组的和为5或10(或者50、100、500、1000等等)。然后再求各组的和,这样计算就简便了。
- 比如,7+1+2=10和2+3=5,所以1+2+2+3+7的结果就是15。
-
分部计算。将数字分成整十数和个位数,然后分别求和。比如,先计算40+30+10,再计算2+5+7,这样计算会比直接计算42+35+17简单。
-
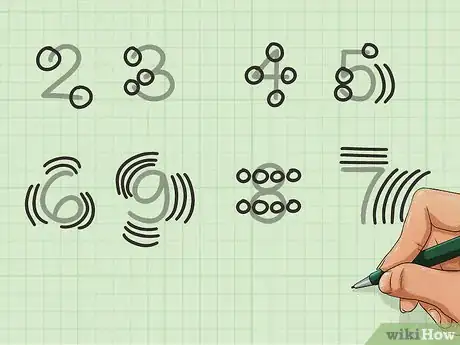
利用数字的形状。如果你想快速心算,那么分组的方法可能并不适合你。你可以利用数字的形状计算加法,而不是靠数手指。这个方法最适合用于几个数字求和的情况。比如:
- 数字2和数字3都有两个终点。
- 数字4和5都有各自的终点数和部分数,其中5上的圆弧看作是一个部分。
- 像6、7、8、9这样的数字就不那么明显了。 6和9的弧线可以看作为3个点(上、中、下),数两遍就是6,数三遍就是9。数字8中的每个圆的一半都记为1(一共4条),数两遍就是8。数字7上方的短线可以认为有3个点,余下的部分有4个点。
广告
小提示
- 如果加法运算比较复杂有难度(例如计算22+47的和),那么你需要学习更多高级的加法计算方法。
- 如果加法运算非常简单,比如计算10以下的运算(如2+5)时,你可以不用笔算,用手指计数即可。
- 当儿童掌握了这个技巧之后,你可以教他们不从数字1开始数,而是从第一个数字开始数。比如8+2,准备两个标记,然后从8开头的数列开始数两次,得到10。这个方法适用于数字的和大于10的情况,当然小于等于10也可以用。
广告
警告
- 尽量不要在学习过程中使用计算器。你可以在计算后使用计算器来检查结果是否正确。但不要在计算过程中屈服于计算器的诱惑而使用计算器。因为,长此以往你会依赖计算器,当你在没有计算器情况下进行加法运算时,你会发现自己常常陷入困境(比如说你正在购物,想大概知道身上带的钱是否足够付你买的物品、鞋子或工具等的帐时,如若不会加法计算,你将会变得很窘迫)。
广告
关于本wikiHow
广告

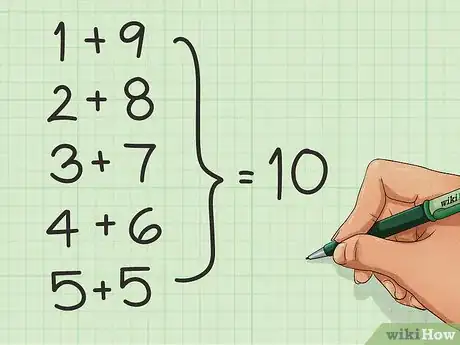

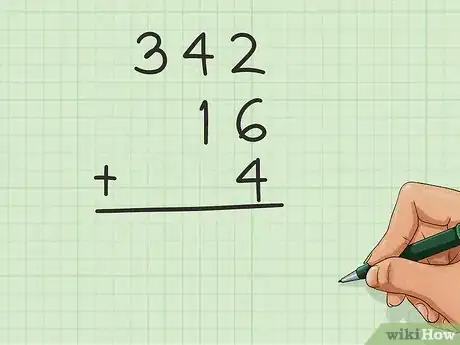
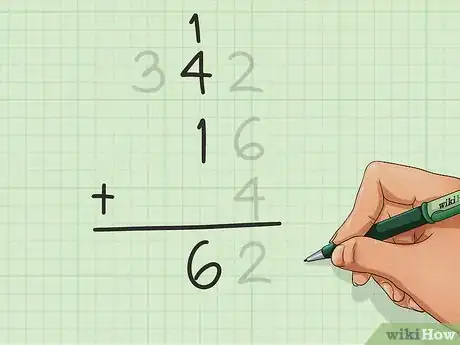
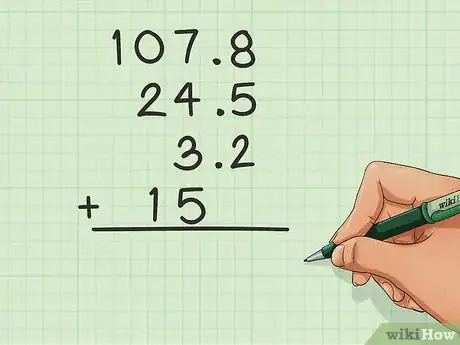
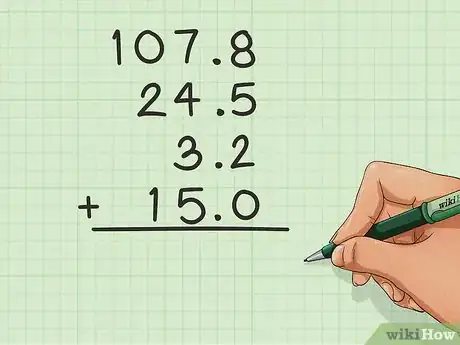
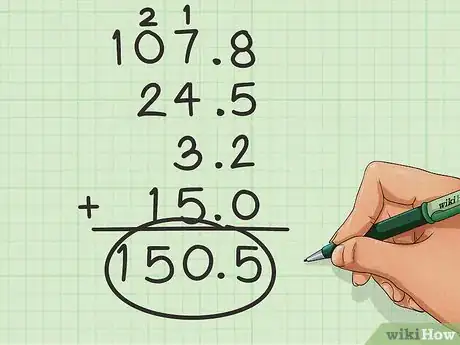
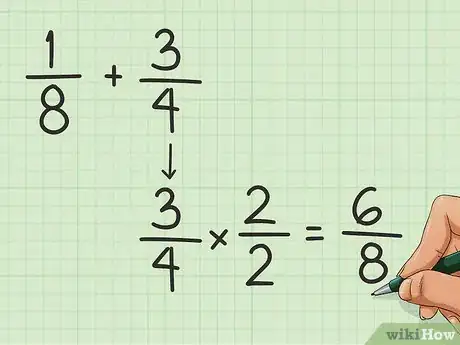
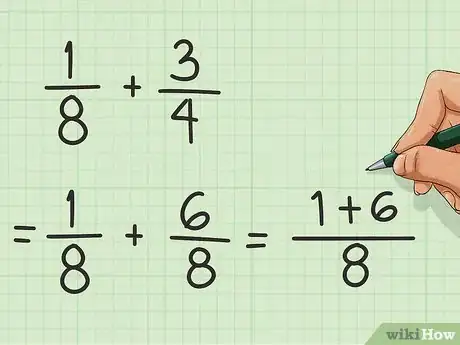
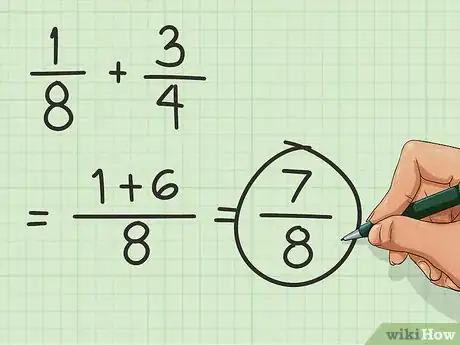
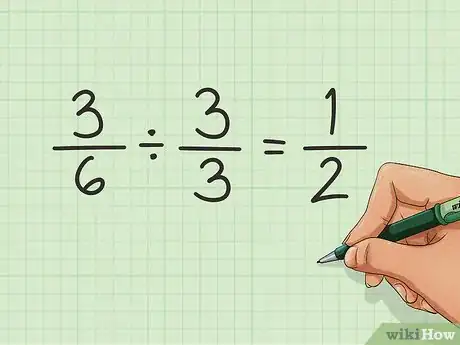
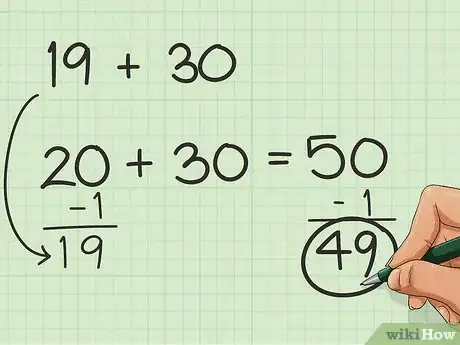
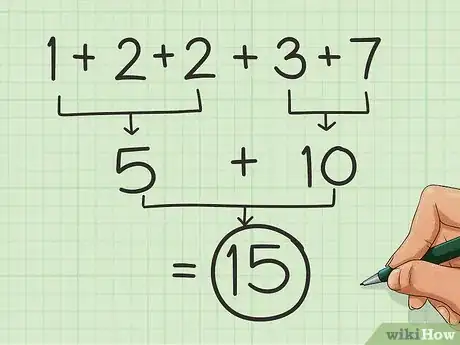
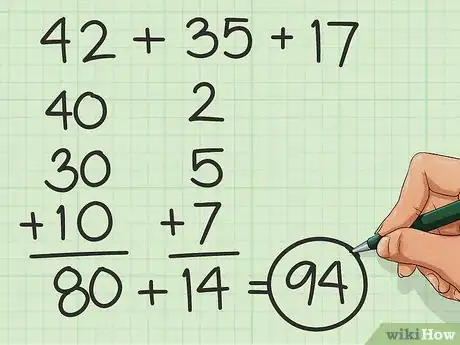







wikiHow的内容管理团队会严密监督编辑人员的工作,确保每篇文章都符合我们的高质量标准要求。 这篇文章已经被读过31,444次。