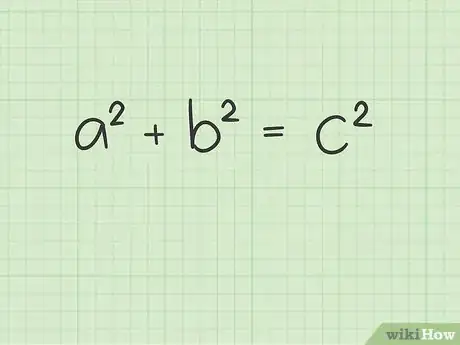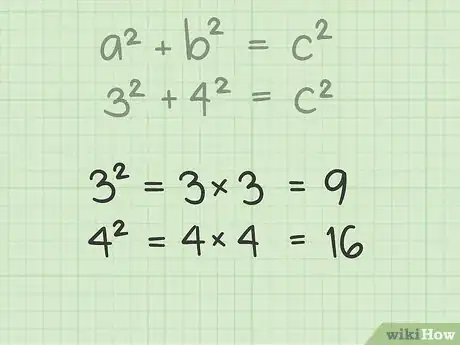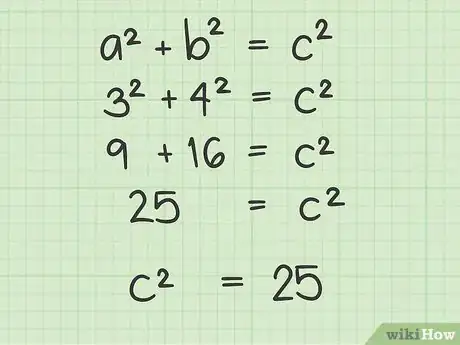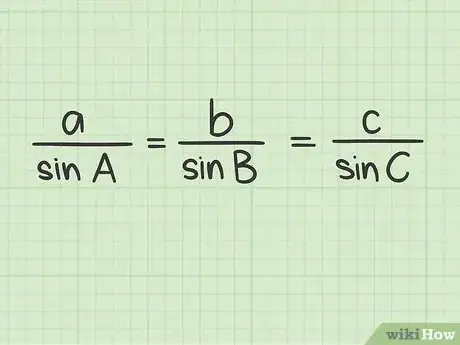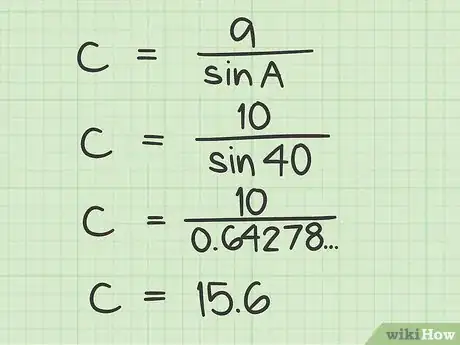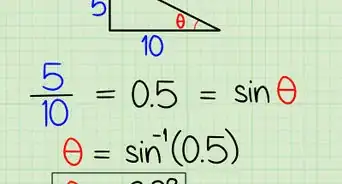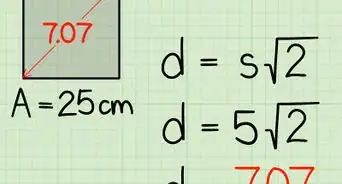X
这篇文章的共同创作者是 Grace Imson, MA. Grace Imson是一位拥有逾40年教学经验的数学老师。她目前是美国旧金山城市学院的数学老师,之前曾在圣路易斯大学的数学系就职。Grace教过小学、初中、高中和大学水平的数学。她拥有圣路易斯大学的教育文学硕士学位,专攻教育管理与监督。
本文引用了9条参考,详情参见页面底部。
这篇文章已经被读过282,417次。
所有直角三角形都有一个90度的直角,斜边是这个直角的对边,也是直角三角形最长的一条边。[1] 有几种不同的方法都能很方便地算出斜边的长度。本文将教你如何在已知三角形两条直角边的边长情况下,利用勾股定理来计算斜边的长度。然后,我们会教你识别某些经常出现在考试中的特殊三角形的斜边。最后,你会学到在已知一条边的边长和一个角的角度时,如何利用正弦定理来求出斜边的长度。
步骤
方法 1
方法 1 的 3:
使用勾股定理
-
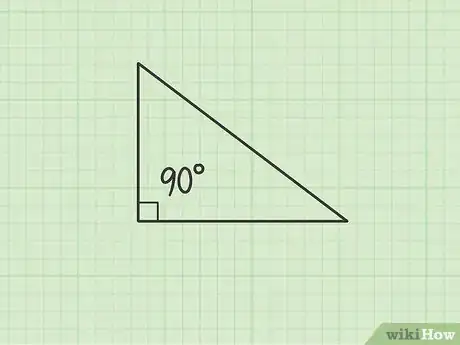
一定要是直角三角形。勾股定理只适用于直角三角形,而且根据定义,只有直角三角形才有斜边。如果你的三角形有一个角正好等于90度,那它就是直角三角形,你可以继续使用以下方法。
- 在教科书和考试中,通常会在角顶端画一个小方块,将直角标示出来。这个特殊的符号代表“90度”。
-
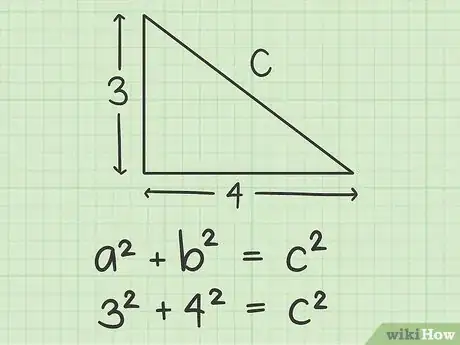
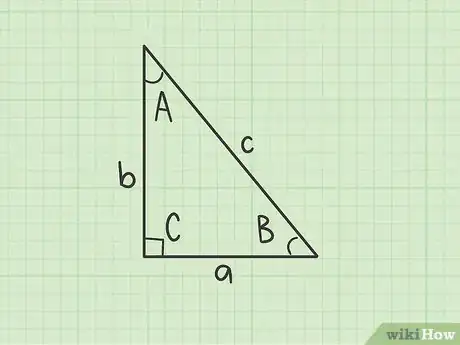
将变量a、b、c赋予三角形的三条边。变量“c”必须赋予斜边,也就是最长的那条边。选另两条边中的一条做“a”,剩下一条做“b”。怎样选择都没关系,都不会影响最终的计算结果。然后将a和b的长度代入公式中,如下所示:
- 如果三角形直角边的边长是3和4,并且你让a = 3,b = 4,则可得到等式:32 + 42 = c2。
-
求a和b的平方。一个数的平方等于它和自己相乘,即a2 = a x a。算出a和b的平方,将它写入你的公式中。
- 如果a = 3,则a2 = 3 x 3,即9。如果b = 4,则b2 = 4 x 4,即16。
- 将以上值代入等式,可得出:9 + 16 = c2。
-
将a2和b2的值相加求和。将结果代入等式,可以算出c2的值。还剩最后一步你就能算出斜边的长度了!
- 在本例中,9 + 16 = 25,因此你可以写下25 = c2。
-
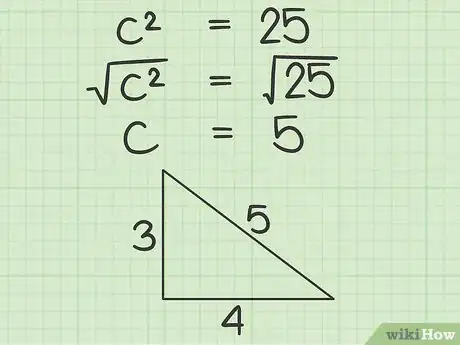
求c2的平方根。使用计算器的平方根功能,或依靠你记忆中的乘法表,算出c2的平方根。得到的结果就是斜边的长度!
- 在本例中,c2 = 25。25的平方根是5。因为5 x 5 = 25,所以Sqrt(25) = 5。也就是说c = 5,这就是斜边的长度!
广告
方法 2
方法 2 的 3:
求特殊直角三角形的斜边
-
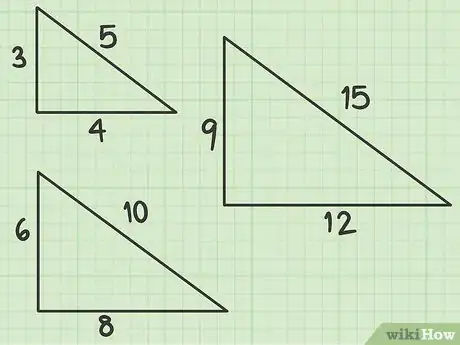
学习识别勾股数三角形。勾股数三角形的边长是符合勾股定理的整数。这些特殊的三角形经常出现在几何课本和SAT、GRE等标准化的考试中。记得前两个勾股数,你就能在这些考试中节约很多时间,因为只要一看到直角边的边长,你就能立即知道这些三角形斜边的长度![4]
- 第一组勾股数是3-4-5(32 + 42 = 52,9 + 16 = 25)。如果直角边的边长为3和4时,不用进行任何计算,你就能确定斜边的边长等于5。
- 即使各边边长都乘以另一个数字,勾股数的的比值仍然成立。例如,直角边的边长为6和8的直角三角形,斜边的长度为10(62 + 82 = 102,36 + 64 = 100)。9-12-15,甚至1.5-2-2.5,这些都是成立的。试着自己算一算,来验证一下吧!
- 考试中经常出现的第二组勾股数是5-12-13 (52 + 122 = 132,25 + 144 = 169)。你还应该注意这组勾股数的倍数,如10-24-26和2.5-6-6.5。
-
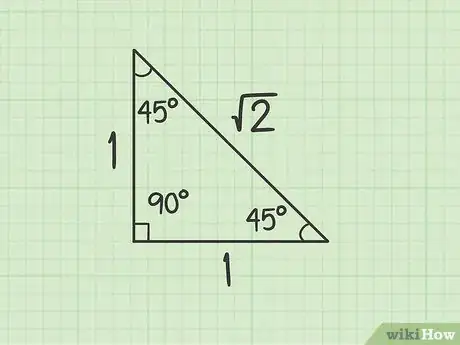
记住45-45-90直角三角形的边长比。45-45-90直角三角形的三个角分别为45度、45度和90度,也被称为等腰直角三角形。它经常出现在标准考试中,相关题目非常容易解答。这类三角形的边长之比为1:1:Sqrt(2),也就是说两条直角边的边长相等,斜边的长度等于直角边的长度乘以2的平方根。
- 要根据一条直角边的长度计算其斜边的长度,用直角边的边长乘以Sqrt(2)就可以了。[5]
- 当考试或作业的题目以变量形式,而非整数形式给出边长时,记住这个比例会很有用。
-
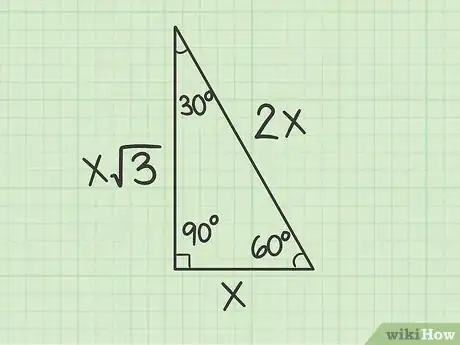
了解30-60-90直角三角形的边长比。这类三角形三个角的度数分别为30度、60度和90度,将等边三角形切成两半,得到的就是这种三角形。30-60-90直角三角形的边长之比始终等于1:Sqrt(3):2,即x:Sqrt(3)x:2x。如果题目告诉你30-60-90直角三角形一条直角边的长度,要你求斜边的长度,那计算起来非常简单:[6]
- 如果已知的是较短直角边的边长,即30度角对边的边长,用该边长乘以2,就可以算出斜边的长度。例如,如果较短直角边的边长为4,你就知道斜边的长度一定等于8。
- 如果已知的是较长直角边的边长,即60度角对边的边长,用该边长乘以2/Sqrt(3),就可以算出斜边的长度。例如,如果较长直角边的边长为4,你就知道斜边的长度一定等于4.62。
广告
方法 3
方法 3 的 3:
用正弦定理求斜边边长
-
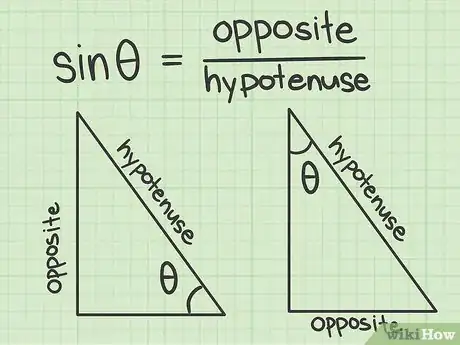
理解“正弦”的定义。“正弦”、“余弦”和“正切”这些术语都是指的三角形的角和(或)边之间的各种比率。在直角三角形中,角的“正弦”被定义为角的对边长度除以三角形的斜边长度。在方程式和计算器中,正弦的缩写是sin。[7]
-
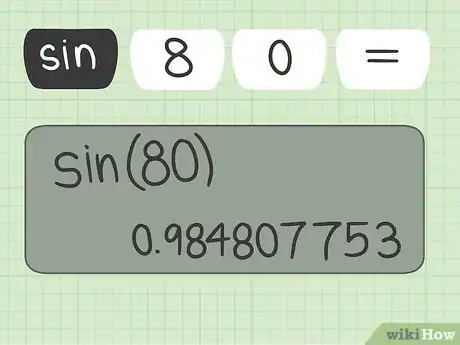
学习计算正弦。即使是最基础的科学计算器也能算正弦函数。寻找标有sin的按键。要计算一个角的正弦,通常要先按sin键,然后输入角的角度值。但是,在某些计算器上,你必须先输入角的角度值,然后再按sin键。你可以用自己的计算器做实验,或查阅说明书,来确定它的步骤顺序。
- 要计算80度角的正弦,你可以输入sin 80,然后按等号或回车键,或者输入80 sin。(计算结果是-0.9939)。
- 你还可以在网页搜索中输入“正弦计算器”,找到一些易于使用的计算器,避免自己去猜答案。[8]
-
学习正弦定理。正弦定理是解三角形问题非常实用的工具。特别是当你知道一条边的边长,以及除直角外另一个角的度数时,正弦定理可以帮你计算三角形斜边的边长。对于三条边分别为a、b和c,三个角分别为A、B和C的三角形而言,正弦定律规定:a / sin A = b / sin B = c / sin C。[9]
- 实际上,正弦定理可被用于“任何”三角形的计算问题,但只有直角三角形有斜边。
-
将变量a、b、c赋予三角形的三条边。最长的斜边必须是“c”。为了简单起见,我们将长度已知的那条边作为“a”,另一条边为“b”。然后将变量A、B、C赋予三角形的三个角。与斜边相对的直角为角“C”。与边“a”相对的角是角“A”,与边“b”相对的角是角“B”。
-
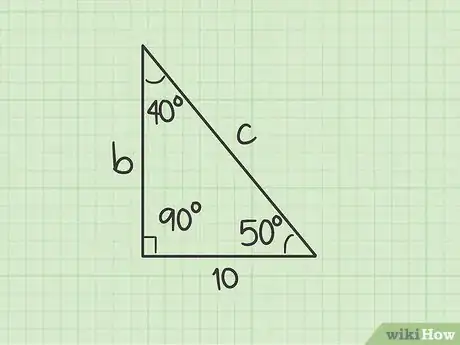
算出第三个角的度数。由于该三角形是直角三角形,所以已知C = 90度,且角A或角B的度数也是已知值。由于三角形的内角和是180度,使用如下公式可以轻易算出第三个角的度数:180 – (90 + A) = B。你还可以将等式变为180 – (90 + B) = A。
- 例如,如果你知道A = 40度,则B = 180 – (90 + 40)。简化后B = 180 – 130,你可以迅速算出B = 50 度。
-
检查你的三角形。此时,你已经知道所有三个角的度数,以及a边的长度。现在将这些信息代入到正弦定理等式中,来计算另两条边的长度。
- 继续使用前文中的例子,假设a边的边长a = 10。角C = 90 度,角A = 40度,而角B = 50度。
-
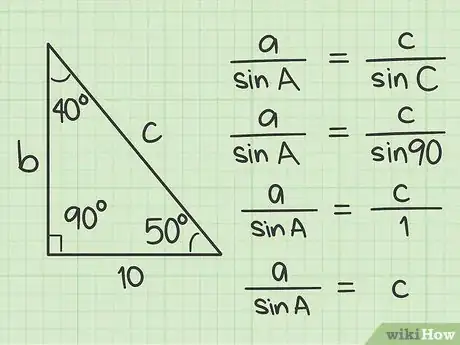
对三角形使用正弦定理。只需要将数字代入到以下等式中,我们就能算出斜边c的长度:A边的长度 / sin A = c边的长度 / sin C。看上去好像还是很难,但90度的正弦是一个常数,恒等于1!因此,等式可以简化为:a / sin A = c / 1,即a / sin A = c。
-
用边a的长度除以角A的正弦,算出斜边的长度。你可以分两步来计算,首先算出sin A,并把它记下来,然后用a除以它。你也可以同时输入到计算器中进行计算。使用计算器时,不要忘了在除号后加上括号。例如,输入10 / (sin 40)或10 / (40 sin),具体如何输入取决于你的计算器。
- 在前文的例子中,我们可以算出sin 40 = 0.64278761。为了求出c的值,只要用a除以这个数字就行了,而10 / 0.64278761 = 15.6,这个答案就是斜边的长度!
广告
参考
- ↑ http://www.mathsisfun.com/definitions/hypotenuse.html
- ↑ http://mathematica.ludibunda.ch/pythagoras6.html
- ↑ https://www.wikihow.com/Use-the-Pythagorean-Theorem
- ↑ http://www.dummies.com/how-to/content/working-with-pythagorean-triple-triangles.html
- ↑ http://www.regentsprep.org/regents/math/algtrig/att2/ltri45.htm
- ↑ http://www.dummies.com/how-to/content/identifying-the-30-60-90-degree-triangle.html
- ↑ https://www.mathsisfun.com/definitions/sine.html
- ↑ http://www.rapidtables.com/calc/math/Sin_Calculator.htm
- ↑ http://www.mathsisfun.com/algebra/trig-sine-law.html
关于本wikiHow
广告