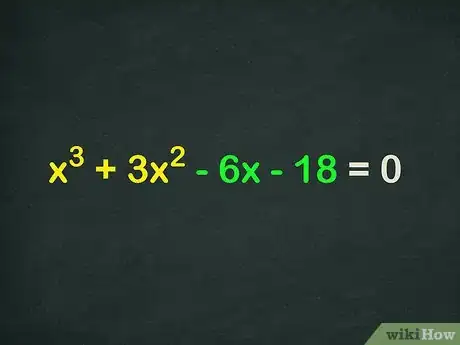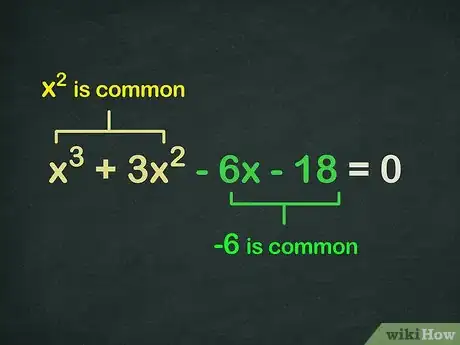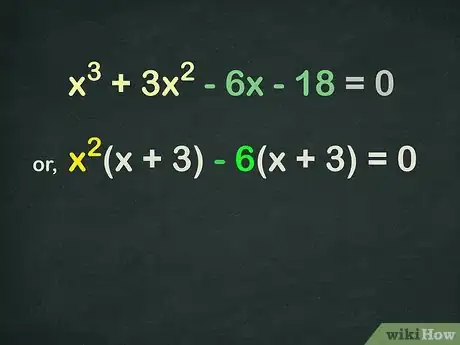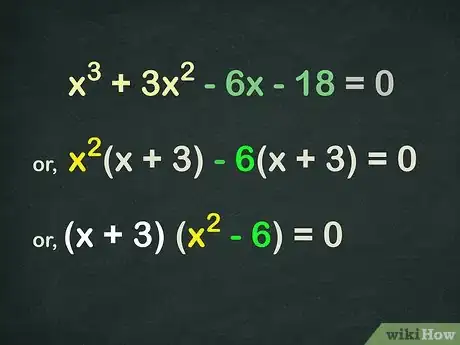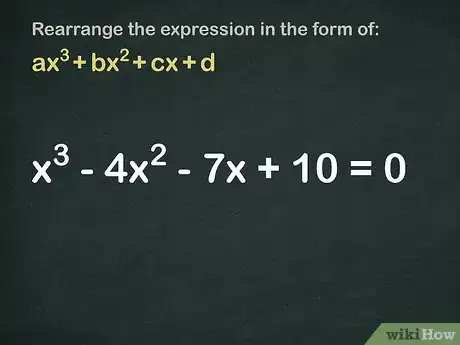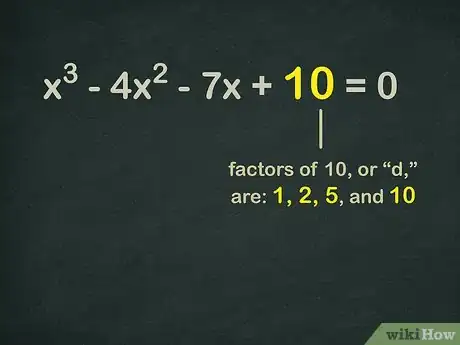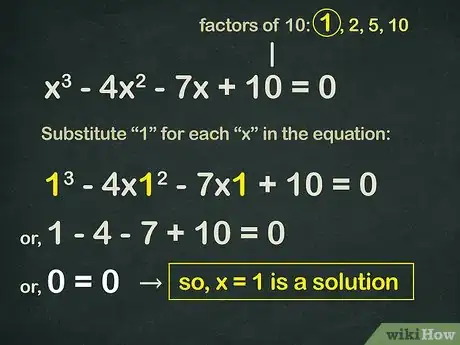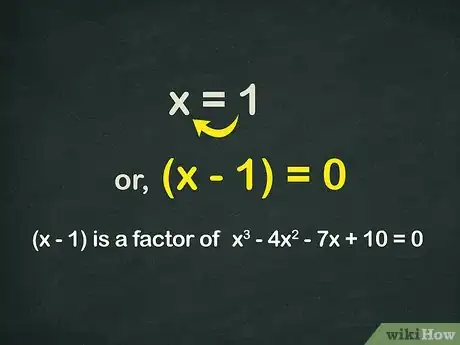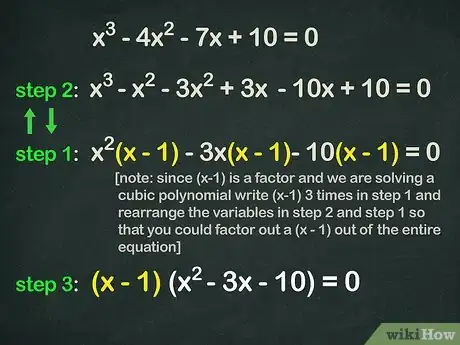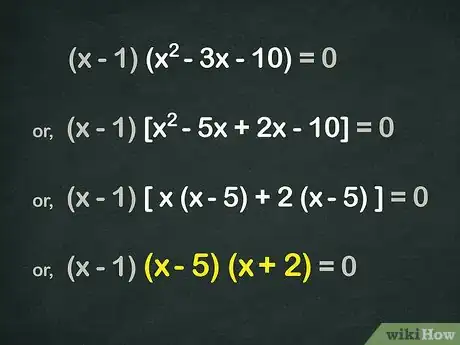X
这篇文章的共同创作者是 Joseph Quinones. Joseph Quinones是南布朗克斯社区特许高中的一位物理教师。他擅长于天文学和天体物理学，并对科学教育和科学推广深感兴趣，目前致力于寻找方法让更多学生可以接触物理学，并希望将更多有色人种学生引入STEM（科学、技术、工程和数学）领域。Joseph曾参与美国自然历史博物馆（AMNH）的天体物理学研究项目。他获得了雷曼学院的物理学学士学位，以及纽约市立学院（CCNY）的物理教育硕士学位。Joseph也是纽约市男性教师联盟（New York City Men Teach）的成员。
这篇文章已经被读过316,826次。
这篇文章教你怎么因式分解三次多项式。我们要学会如何用组合方法和因式分解自由项的方法来解这类问题。
步骤
部分 1
部分 1 的 2:
通过组合来分解
部分 2
部分 2 的 2:
利用自由项
-
把多项式整理为ax3+bx2+cx+d。[4]
- 比如要分解多项式：x3 - 4x2 - 7x + 10 = 0。
-
把所有 "d"的因数找出来。常数"d"是不含如"x"变量的数。
- 因数就是可以相乘得到另一个数的数。这里，10或 "d"的因数是: 1、 2、 5 和 10。
-
找出一个因子，让多项式等于零。当用d的因数替代"x"时，我们要看看哪个符合方程的解。
- 试试第一个因数 1 ，把x替换掉，得到 (1)3 - 4(1)2 - 7(1) + 10 = 0
- 得到 1 - 4 - 7 + 10 = 0。
- 因为 0 = 0 是真实的，所以x = 1 是一个解。
-
重新整理一下，如果x = 1，可以把整个方程改一下面目。
- "x = 1" 等价于"x - 1 = 0" 或 "(x - 1)" 。我们刚刚从每边都减掉了一个1。
-
把剩余的因数都分解出来。 "(x - 1)" 是我们的一个根，看看能不能把剩余的解都提出来，一次解决一个多项式。
- 可不可以把(x - 1) 从 x3 提出来？ 不行，但是可以从第二项借一个 -x2 ，分解为 x2(x - 1) = x3 - x2。
- 可不可以把(x - 1) 从剩余部分提出来？不行，要从第三项 -7x 借一个 3x。于是得到-3x(x - 1) = -3x2 + 3x。
- 因为 -7x 中提取出一个 3x，第三项变为 -10x ，而我们的常数是10。可以分解吗？可以！ -10(x - 1) = -10x + 10。
- 我们改变了一些变量，让其可以分解出 (x - 1) 。重新整理的方程是这样的： x3 - x2 - 3x2 + 3x - 10x + 10 = 0 ，但和原先 x3 - 4x2 - 7x + 10 = 0 没什么差别。
-
继续用自由项因数因式分解。仔细观察我们在第五步中用(x - 1) 因式分解出的数字：
- x2(x - 1) - 3x(x - 1) - 10(x - 1) = 0。可以重新整理，要再一次分解容易得多: (x - 1)(x2 - 3x - 10) = 0。
- 只需要因式分解(x2 - 3x - 10) ，得到(x + 2)(x - 5)。
-
于是得到的解就是之前算出来的因数了。可以把每一项都代回去试试看对不对。
- (x - 1)(x + 2)(x - 5) = 0 表示解是 1、 -2、5。
- 把-2 代入等式：(-2)3 - 4(-2)2 - 7(-2) + 10 = -8 - 16 + 14 + 10 = 0。
- 把 5 代入等式：(5)3 - 4(5)2 - 7(5) + 10 = 125 - 100 - 35 + 10 = 0。
广告
小提示
- 三次多项式是三个一次多项式的积，或者一个无法分解的二次多项式和一个一次多项式的积。后面的情况，我们将整个等式除以一次多项式得到二次多项式。
- 三次多项式一定能因式分解得出实数解，因为每个三次项都一定有个实根。三次方多项式如x3 + x + 1含有无理实根，不能被因式分解成含有整数或有理数系数的多项式。虽然可以用立方方程因式分解，这种方程还是不能分解成一个“整数”多项式。[5]
广告
参考
- ↑ http://web.math.ucsb.edu/~vtkala/2016/S/4B/FactoringCubicPolynomials.pdf
- ↑ https://sciencing.com/solve-cubic-polynomials-2409.html
- ↑ https://www.mathsisfun.com/algebra/polynomials-solving.html
- ↑ https://www.dummies.com/education/math/pre-calculus/factoring-four-or-more-terms-by-grouping/
- ↑ https://kipkis.com/Factor_a_Cubic_Polynomial
关于本wikiHow
Joseph Quinones
高中物理老师
这篇文章的共同创作者是 Joseph Quinones. Joseph Quinones是南布朗克斯社区特许高中的一位物理教师。他擅长于天文学和天体物理学，并对科学教育和科学推广深感兴趣，目前致力于寻找方法让更多学生可以接触物理学，并希望将更多有色人种学生引入STEM（科学、技术、工程和数学）领域。Joseph曾参与美国自然历史博物馆（AMNH）的天体物理学研究项目。他获得了雷曼学院的物理学学士学位，以及纽约市立学院（CCNY）的物理教育硕士学位。Joseph也是纽约市男性教师联盟（New York City Men Teach）的成员。 这篇文章已经被读过316,826次。
分类: 教育与交流
广告
