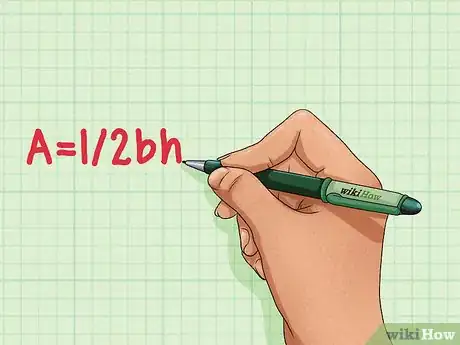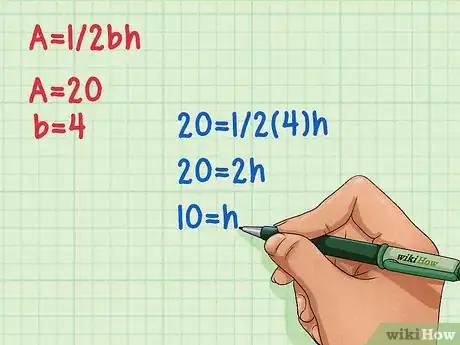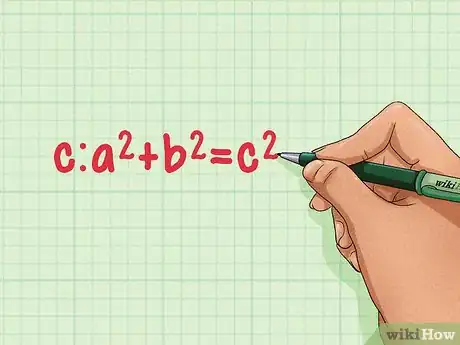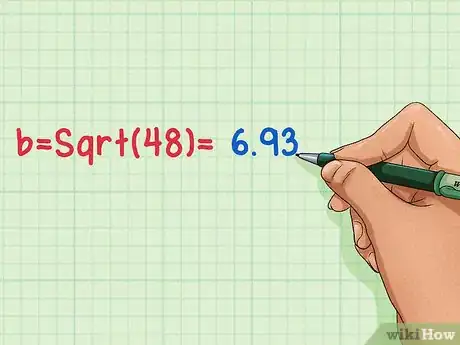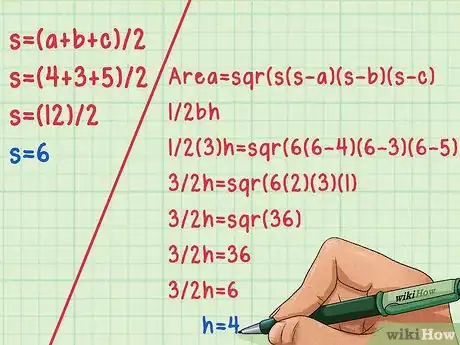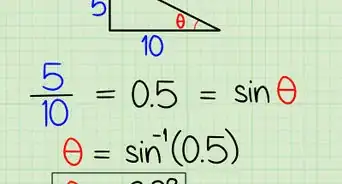X
wikiHow是一个“多人协作写作系统”,因此我们的很多文章都是由多位作者共同创作的。 为了创作这篇文章,26位用户(部分匿名)多次对文章进行了编辑和改进。
这篇文章已经被读过390,521次。
在计算三角形的面积时,你需要知道三角形的高。如果三角形的高不是已知信息,那么需要你根据已知条件求出这个三角形的高。根据不同的已知条件,本文将展示多种不同的求解三角形高度的方法,让我们一起来学习吧!
步骤
方法 1
方法 1 的 3:
已知面积和底边长求高
-
回想三角形的面积公式。三角形的面积公式是A=1/2bh。[1]
- A = 三角形的面积
- b = 三角形底边长
- h = 三角形底边的高
-
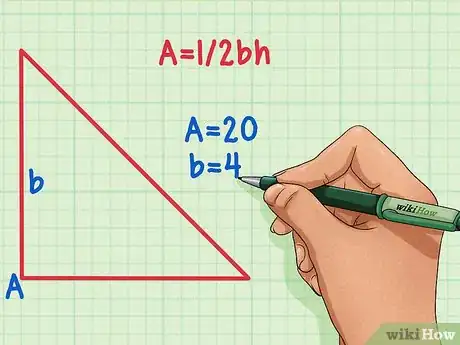
看一下你的三角形,确定哪些变量是已知的。 在本例中,你已经知道了面积,可以将面积的数值代入公式中的A。你也已知底边长的大小,可以将数值代入公式中的"'b'"。如果你不知道面积或底边长,那么你只能尝试其它的方法了。
- 无论三角形是如何绘制的,三角形的任意一边都可以作为底边。为了更形象地展示它,你可以想象把三角形进行旋转,直到已知边长位于底部。
- 例如,如果已知三角形面积是20,一边长为4,那么带入得A = 20,b = 4。
-
将数值代入公式A=1/2bh,然后进行计算。首先将底边长(b)乘以1/2,然后用面积(A)除以它。运算得到的结果应该就是三角形的高!
- 本例中:20 = 1/2(4)h
- 20 = 2h
- 10 = h
广告
方法 2
方法 2 的 3:
求等边三角形的高
-
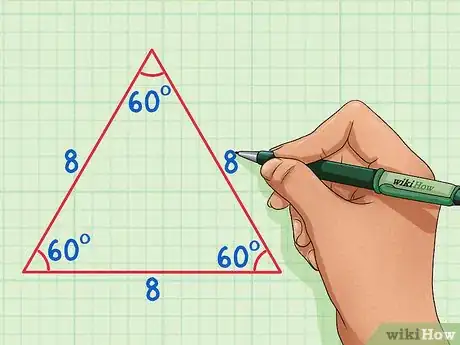
回忆等边三角形的特征。等边三角形有三条相等大小的侧边,每个夹角都是60度。如果你将等边三角形分成两半,就会得到两个相同的直角三角形。[2]
- 在本例中,我们使用边长为8的等边三角形。
-
回忆勾股定理。勾股定理将两个直角边描述为a和b、斜边为c:a2 + b2 = c2。我们可以使用这个定理求出等边三角形的高![3]
-
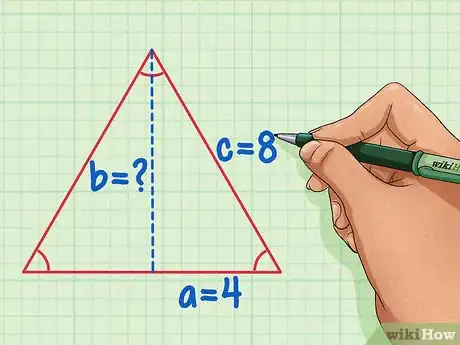
将等边三角形对半切开,并将数值代入变量a、b和c。斜边c等于原始的斜边长。直角边a的长度就变成了边长的1/2,直角边b就是所求的三角形的高。
- 以边长为8的等边三角形为例,其中c = 8,a = 4。
-
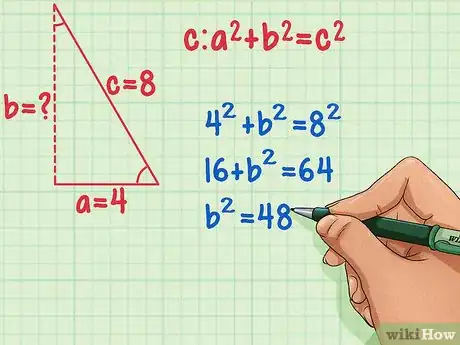
将数值代入勾股定理的公式,求出b2。边长c和a分别乘以自身求平方值。 然后用c2减去a2。
- 42 + b2 = 82
- 16 + b2 = 64
- b2 = 48
-
求出b2的开方值就得到三角形的高了!使用计算机的开根号计算求得Sqrt(2)。得到的结果就是等边三角形的高!
- b = Sqrt (48) = 6.93
广告
方法 3
方法 3 的 3:
已知边长和角求高
-
确定你已知的变量。如果你知道三角形的一个夹角和一条边长,如果这个角是底边和已知侧边的夹角,或是已知三条边长,你就能求出三角形的高。我们将三角形的三边称之为a、b和c,三角为A、B和C。
- 如果你已知三角形的三边边长,可以使用海伦公式来求出三角形的高。
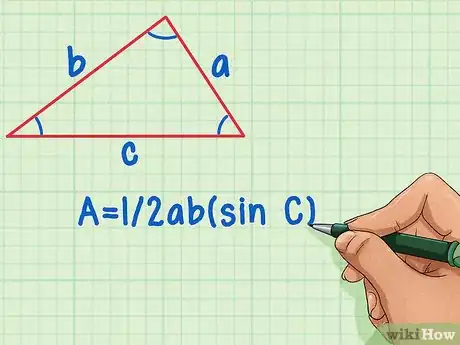
- 如果你已知两条边长和一个角,可以使用面积公式A = 1/2ab(sin C)来求解。[4]
-
如果你已知三条边长也可以使用海伦公式。海伦公式分为两部分。首先,你必须求解出变量 s,它等于三角形周长的一半。你可以使用这个公式:s = (a+b+c)/2 求出。[5]
- 例如,三角形三边长为 a = 4、b = 3和c = 5,故而s = (4+3+5)/2,也就是s = (12)/2。求出s = 6。
- 然后使用海伦公式的第二部分。面积 = sqr(s(s-a)(s-b)(s-c)。 再将面积代入含有高的面积公式:1/2bh (或 1/2ah 、1/2ch)。
- 计算求出高。在本例中,就是1/2(3)h = sqr(6(6-4)(6-3)(6-5)。化简得3/2h = sqr(6(2)(3)(1),也就是3/2h = sqr(36)。使用计算器计算开方,得到3/2h = 6。因此,使用边长b作为底边,得出,三角形的高等于4。
-
如果已知一条边长和一个夹角,使用两边和一角的面积公式来求解。用三角形面积公式1/2bh来代替上述公式中的面积。公式就变成了1/2bh = 1/2ab(sin C),化简得到h = a(sin C),这样可以消除一条未知边长的变量。[6]
- 根据已知变量来求解等式。例如,已知a = 3、C = 40度,代入公式得“h = 3(sin 40)。使用计算器来计算等式,得到高h约等于1.928。
广告
参考
- ↑ http://www.mathsisfun.com/algebra/trig-area-triangle-without-right-angle.html
- ↑ http://www.mathsisfun.com/definitions/equilateral-triangle.html
- ↑ http://www.mathsisfun.com/pythagoras.html
- ↑ http://www.mathsisfun.com/algebra/trig-area-triangle-without-right-angle.html
- ↑ http://www.mathsisfun.com/geometry/herons-formula.html
- ↑ http://www.mathsisfun.com/algebra/trig-area-triangle-without-right-angle.html
关于本wikiHow
广告