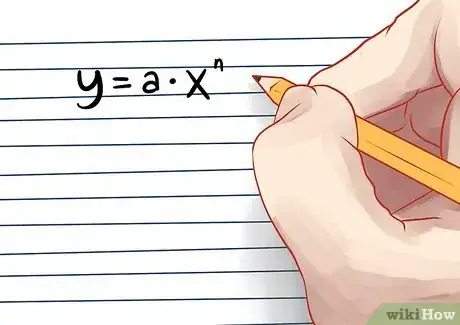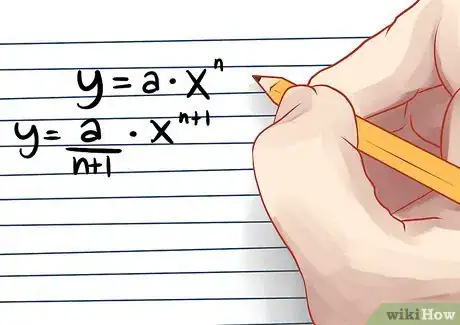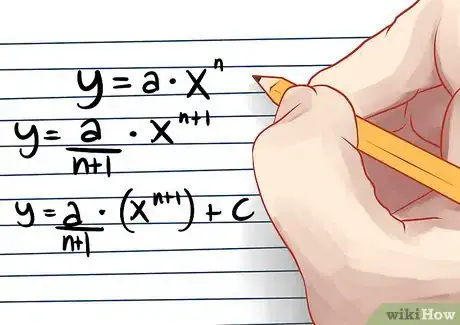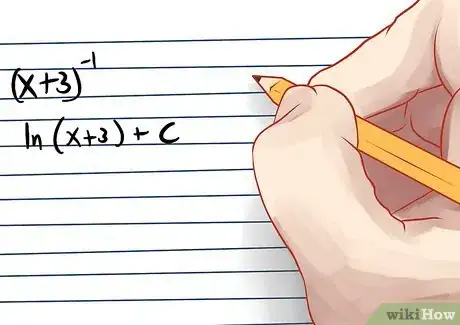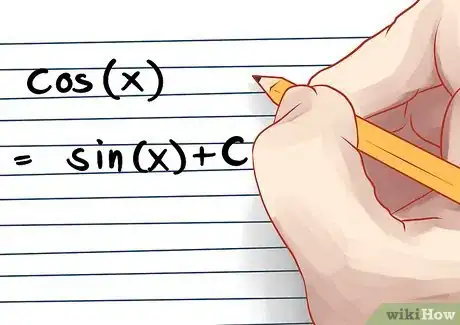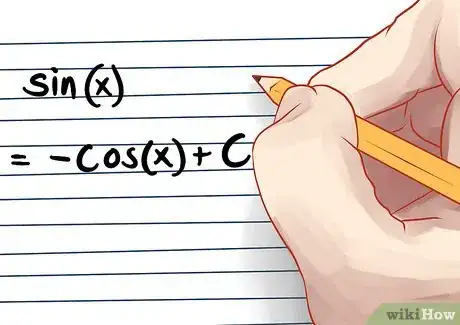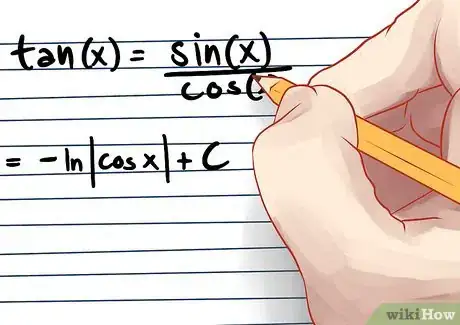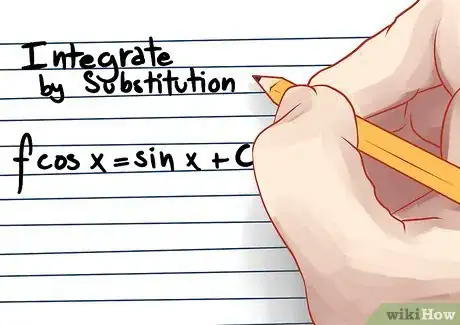X
wikiHow是一个“多人协作写作系统”,因此我们的很多文章都是由多位作者共同创作的。 为了创作这篇文章,志愿作者多次对文章进行了编辑和改进。
这篇文章已经被读过44,098次。
积分算是微分的逆运算,积分可以用来计算曲线下的面积。多项式的类型不同,积分的公式也不同。
步骤
方法 1
方法 1 的 2:
简单的积分
-
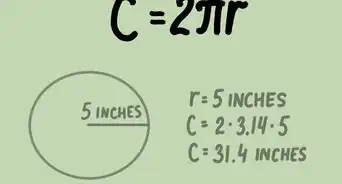
大多数多项式适用的积分公式。比如多项式:y = a*x^n.
-
系数除以(n+1),然后指数加上1。换句话说y = a*x^n 的积分是y = (a/n+1)*x^(n+1).
-
对于不定积分,一个多项式对应多个,所以要加上积分常数C。因此本例的最终结果是y = (a/n+1)*x^(n+1) + C。
- 考虑这样一个问题:在计算微分是,所有常数项都被省略。因此,在求积分时,积分结果可以加上任意的常数。
-
根据这个公式,计算积分。比如,y = 4x^3 + 5x^2 +3x 的积分是(4/4)x^4 + (5/3)*x^3 + (3/2)*x^2 + C = x^4 + (5/3)*x^3 + (3/2)*x^2 + C.广告
方法 2
方法 2 的 2:
其他公式
关于本wikiHow
广告