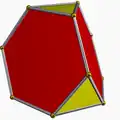
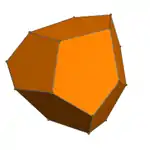
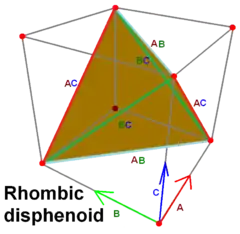
三角化四面體
在幾何學中,三角化四面體(英語:triakis tetrahedron或kistetrahedron[2])是一種卡塔蘭多面體,其為截角正四面體的對偶多面體[3]。
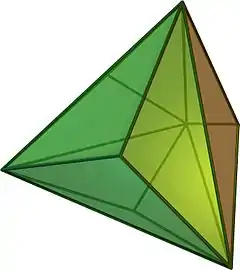 () | |||
| 類別 | 卡塔蘭立體 | ||
|---|---|---|---|
| 對偶多面體 | 截角正四面體 | ||
| 識別 | |||
| 鮑爾斯縮寫 | tikit | ||
| 數學表示法 | |||
| 考克斯特符號 | |||
| 性質 | |||
| 面 | 12 | ||
| 邊 | 18 | ||
| 頂點 | 8 | ||
| 歐拉特徵數 | F=12, E=18, V=8 (χ=2) | ||
| 二面角 | 129° 31' 16" | ||
| 組成與佈局 | |||
| 面的種類 | 等腰三角形 | ||
| 面的佈局 | V3.6.6 | ||
| 頂點圖 | 4{3}+4{6} | ||
| 對稱性 | |||
| 對稱群 | Td, A3, [3,3], *332 | ||
| 旋轉對稱群 | T, [3,3]+, 332 | ||
| 特性 | |||
| 凸、face-transitive | |||
| 圖像 | |||
| |||
性質

三角化四面體是一種卡塔蘭立體,由12個面、18條邊和8個頂點組成[7],對偶多面體是一個阿基米德立體——截角四面體[7][3]。由於其對偶多面體具有點可遞的性質,因此三角化四面體擁有面可遞的性質,即所有面皆全等。三角化四面體由12個全等的等腰三角形組成,其頂點有兩種:一種為3個等腰三角形的公共頂點,另一種為6個等腰三角形的公共頂點。
三角化四面體可以看做是在正四面體每個面上加上錐高為倍邊長的三角錐後所形成的形狀[8],可以視為正三角形三邊各加一個等腰三角形拼成的正六邊形在立體幾何中的推廣。
正交投影
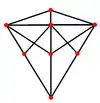
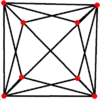
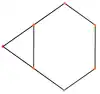
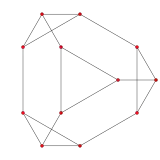
三角化四面體有4個特殊的正交投影,分別為於稜上投影(兩種)、於面上投影和於面與頂點上投影。
| 投影位置 | 於稜上投影 | 於面上投影 | 於面與頂點上投影 | 於稜上投影(交叉) |
|---|---|---|---|---|
| 三角化 四面體 |
 |
 |
 |
 |
| (對偶) 截角 四面體 |
 |
 |
 |
 |
| 投影 對稱性 |
[1] | [1] | [3] | [4] |
相關多面體與鑲嵌

三角化四面體是正四面體經過三角化變換後的結果,其他也是由正四面體透過康威變換得到的多面體有:
| 对称性: [3,3], (*332) | [3,3]+, (332) | ||||||
|---|---|---|---|---|---|---|---|
 |
 |
 |
 |
 | |||
| {3,3} | t0,1{3,3} | t1{3,3} | t1,2{3,3} | t2{3,3} | t0,2{3,3} | t0,1,2{3,3} | s{3,3} |
| 半正多面体对偶 | |||||||
 |
 |
 |
 | ||||
| V3.3.3 | V3.6.6 | V3.3.3.3 | V3.6.6 | V3.3.3 | V3.4.3.4 | V4.6.6 | V3.3.3.3.3 |
三角化四面體是由等腰三角形組成,且對偶多面體由正六邊形與正三角形交錯組成。同樣由等腰三角形組成,且對偶多面體由正多邊形與正三角形交錯組成的多面體或鑲嵌圖包括:
| 對稱性 *n32 [n,3] |
球面鑲嵌 | 歐氏鑲嵌 | 緊湊雙曲 | 非緊雙曲 | ||||
|---|---|---|---|---|---|---|---|---|
| *232 [2,3] |
*332 [3,3] |
*432 [4,3] |
*532 [5,3] |
*632 [6,3] |
*732 [7,3] |
*832 [8,3]... |
*∞32 [∞,3] | |
| 截角鑲嵌 |  |
 |
 |
 |
 |
 |
 |
 |
| 頂點 | 3.4.4 | 3.6.6 | 3.8.8 | 3.10.10 | 3.12.12 | 3.14.14 | 3.16.16 | 3.∞.∞ |
| 三角化 鑲嵌 |
 |
 |
 |
 |
 |
 | ||
| 頂點 | V3.4.4 | V3.6.6 | V3.8.8 | V3.10.10 | V3.12.12 | V3.14.14 | V3.16.16 | V3.∞.∞ |
對偶複合體
 複合截角四面體三角化四面體 | |
| 類別 | 複合半正多面體 |
|---|---|
| 對偶多面體 | 自身對偶 |
| 性質 | |
| 體 | 2 |
| 面 | 20 |
| 邊 | 36 |
| 頂點 | 20 |
| 歐拉特徵數 | F=20, E=36, V=20 (χ=4) |
| 組成與佈局 | |
| 複合幾何體數量 | 2 |
| 複合幾何體種類 | 1個三角化四面體 1個截角四面體 |
| 面的種類 | 12個等腰三角形 4個正三角形 4個正六邊形 |
| 對稱性 | |
| 對稱群 | 四面體群 (Td) |
對偶複合體,即一個多面體與其對偶多面體組合成的複合圖形。三角化四面體與其對偶的複合體為複合截角四面體三角化四面體。其共有20個面、36條邊和20個頂點,其尤拉示性數為4,虧格為-1[11]。
 以正六邊形面為中心 |
 以正三角形面為中心 |
- 面的組成
複合截角四面體三角化四面體由4個正三角形、4個正六邊形和12個等腰三角形組成,其中組成的等腰三角形與三角化四面體完全相同,邊長比同為3:3:5,但有部分隱沒在截角四面體中,如下圖所示,露在該立體外部的部分,以藍色表示,隱沒在立體內部的部分以白色表示,其中黑線代表等腰三角形與其對偶多面體截角四面體相交的位置:
複合截角四面體三角化四面體中的截角四面體亦有部分隱沒在三角化四面體中,如下圖所示:
 正六邊形面 |
 正三角形面 |
參見
註解
- 使用wolframalpha計算: (页面存档备份,存于)
參考文獻
- Williams, Robert. . Dover Publications, Inc. 1979. ISBN 0-486-23729-X. (Section 3-9)
- Wenninger, Magnus, , Cambridge University Press, 1983, ISBN 978-0-521-54325-5, MR 0730208, doi:10.1017/CBO9780511569371 (The thirteen semiregular convex polyhedra and their duals, Page 14, Triakistetrahedron)
- The Symmetries of Things 2008, John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, ISBN 978-1-56881-220-5 (Chapter 21, Naming the Archimedean and Catalan polyhedra and tilings, page 284, Triakis tetrahedron)
- Conway, Symmetries of things[1], p.284
- Holden, A. Shapes, Space, and Symmetry. New York: Columbia University Press, p. 55, 1971., p. 55
- . 國家教育研究院. [2018-08-23]. (原始内容存档于2018-08-26).
- Correns, C. W. . Berlin: Springer-Verlag. 1949: p. 41.
- Berry, L. G. and Mason, B. Mineralogy: Concepts, Descriptions, Determinations. San Francisco, CA: W. H. Freeman, 1959., p. 127
- . bulatov.com. [2018-08-26]. (原始内容存档于2017-12-06).
- Weisstein, Eric W. (编). . at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. (英语).
- . rechneronline.de. [2018-08-26]. (原始内容存档于2017-10-02).
- . dmccooey.com. [2018-08-26]. (原始内容存档于2018-01-27).
- . bulatov.org. [2018-08-26]. (原始内容存档于2017-12-06).
- Weisstein, Eric W. (编). . at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. (英语).
- . 國家教育研究院. [2018-08-23]. (原始内容存档于2018-08-26).