曲线积分

在数学中，线积分（英語：）[註 1]是积分的一种。积分函数的取值沿的不是区间，而是被称为积分路径的特定曲线。[註 2]

在曲线积分中，被积的函数可以是标量函数或向量函数。當被積函數是純量函數時，积分的值是積分路径各点上的函数值乘上該點切向量的長度，在被积分函数是向量函数时，積分值是積分向量函数与曲线切向量的內積。在函數是純量函數的情形下，可以把切向量的絕對值（長度）看成此曲線把該點附近定義域的極小區間，在對應域內拉長了切向量絕對值的長度，這也是曲线积分与一般区间上的积分的主要不同点。物理学中的许多簡潔公式（例如W=F·s）在推广之后都是以曲线积分的形式出现

$W=\int _{C}\mathbf {F} \cdot \mathrm {d} \mathbf {s}$ 。

曲线积分在物理学中是很重要的工具，例如计算电场或重力场中的做功。

向量分析

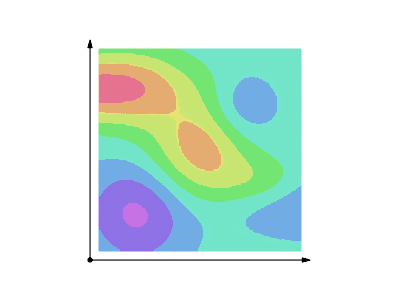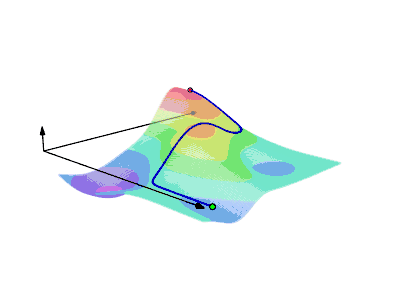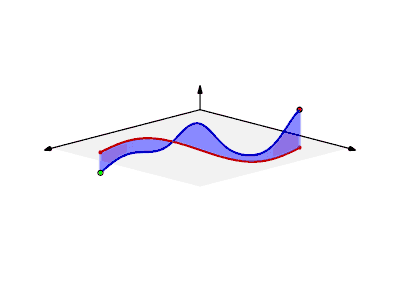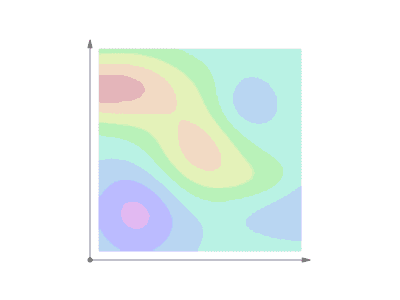
大致來說，向量分析中的曲线积分可以看成在某一场中沿特定路径的累积效果。更具体地说，如果曲線 $C\subseteq \mathbb {R} ^{2}$ ，标量场的曲线积分可以想成某個曲线（不是 ${\textstyle C}$ ）向下切割出的面积，这可以通过建立函數z = f(x,y)和x-y平面内的曲线C来想像這個曲面，可以把 $x{\text{-}}y$ 平面上的曲線 $C$ 想成屏風的底座， $f$ 代表在該點屏風的高度（這裡假設 $f\geq 0$ ），則 $f$ 的曲线积分就是該“屏風”的面积，也就是前面所說曲線 ${\textstyle (x(t),y(t),f(x,y))}$ 向下切割的面積，其中 ${\textstyle (x(t),y(t))}$ 是曲線 ${\textstyle C}$ 的參數化。

标量场的曲线积分

梯度場中的曲線積分

定义

设有标量场：F : U ⊆ Rⁿ $\to$ R，则对于路径C ⊂ U，F的曲线积分是：

\int _{C}f\,\mathrm {d} s=\int _{a}^{b}f(\mathbf {r} (t))|\mathbf {r} '(t)|\,\mathrm {d} t.

其中，r: [a, b] $\to$ C 是一个一一對應的参数方程，并且r(a)和r(b)分别是路径曲线C的两个端点。

f称为积分函数，C是积分路径。不严格地说，ds可以被看作积分路径上的一段很小的“弧长”。曲线积分的结果不依赖于参量化函数r。

几何上，当标量场f定义在一个平面（n=2）上时，它的图像是空间中一个曲面z=f(x,y)，曲线积分就是以曲线C为界的有符号的截面面积。参见动画演示。

向量场的曲线积分

向量场的曲线积分

设有向量场：F : U ⊆ Rⁿ $\to$ Rⁿ，则其在路径C ⊂ U上关于方向r的曲线积分是：

\int _{C}\mathbf {F} (\mathbf {r} )\cdot \,\mathrm {d} \mathbf {r} =\int _{a}^{b}\mathbf {F} (\mathbf {r} (t))\cdot \mathbf {r} '(t)\,\mathrm {d} t.

其中，r: [a, b] $\to$ C 是一个一一的参量化函数，并且r(a)和r(b)分别是路径曲线C的两个端点。这时曲线积分值的绝对值与参量化函数r无关，但其方向与参量化函数r的选择有关。特别地，当方向相反时，积分值也相反。

与路径无关的条件

如果向量场F是一个标量场G的梯度，即：

\nabla G=\mathbf {F} ,

那么，由G和r组成的复合函数的导数是：

{\operatorname {d}  \over \operatorname {d} \!t}G{\bigl (}\mathbf {r} (t){\bigr )}=\nabla G{\bigl (}\mathbf {r} (t){\bigr )}\cdot \mathbf {r} '(t)=\mathbf {F} {\bigl (}\mathbf {r} (t){\bigr )}\cdot \mathbf {r} '(t)

于是对路径C就有：

\int _{C}\mathbf {F} (\mathbf {r} )\cdot \,\mathrm {d} \mathbf {r} =\int _{a}^{b}\mathbf {F} {\bigl (}\mathbf {r} (t){\bigr )}\cdot \mathbf {r} '(t)\,\mathrm {d} t=\int _{a}^{b}{\frac {\mathrm {d} G{\bigl (}\mathbf {r} (t){\bigr )}}{\mathrm {d} t}}\,\mathrm {d} t=G{\bigl (}\mathbf {r} (b){\bigr )}-G{\bigl (}\mathbf {r} (a){\bigr )}

。

用文字表示，就是说若F是一个梯度场，那么F的曲线积分与所取的路径无关，而只与路径的起点和终点的选取有关。

应用

在各种保守力的场都是路径无关的，一个常见的例子就是重力场或电场。在计算这种场的做功时，可以选择适当的路径进行积分，使得计算变得简单。

曲线积分与复分析的关系

如果将复数看作二维的向量，那么二维向量场的曲线积分就是相应复函数的共轭函数在同样路径上的积分值的实部。

根据柯西-黎曼方程，一个全纯函数的共轭函数所对应的向量场的旋度是0。

複曲线积分

在複分析中，曲线积分是通过复数的加法和乘法定义的。令 $U$ 为複数集 $\mathbb {C}$ 的一个开子集， $f:U\to \mathbb {C}$ 是一个函数， $L\subset U$ 是一个参数为 ${\displaystyle \gamma$ 的可求长曲线，其中 $\gamma (t)=x(t)+iy(t)$ 。则曲线积分：

\int _{L}f(z)\,\mathrm {d} z

可以通过将区间 $[a,b]$ 分划为 $a=t_{0}<t_{1}<\cdots <t_{n}=b$ 来定义。考虑下式：

\sum _{k=1}^{n}f(\gamma (t_{k}))[\gamma (t_{k})-\gamma (t_{k-1})]=\sum _{k=1}^{n}f(\gamma _{k})\Delta \gamma _{k}.

曲线积分是区间分划的长度趋于零时这个黎曼和的极限。

当 $\gamma$ 连续可微时，曲线积分可以用一个实变函数的积分表示：

\int _{L}f(z)\,\mathrm {d} z=\int _{a}^{b}f{\bigl (}\gamma (t){\bigr )}\,\gamma \,'(t)\,\mathrm {d} t.

当 $L$ 为闭合曲线时，积分的起点和终点重合，这时 $f$ 沿 $L$ 的曲线积分通常记作

\oint _{L}f(z)\,dz

对于共轭微分算子 ${\overline {dz}}$ 的曲线积分定义为[1]

\int _{L}f{\overline {\mathrm {d} z}}={\overline {\int _{L}{\overline {f}}\mathrm {d} z}}=\int _{a}^{b}f{\bigl (}\gamma (t){\bigr )}\,{\overline {\gamma '(t)}}\,\mathrm {d} t.

複函数的曲线积分有很多技巧。将複函数分作实部和虚部，可以将问题简化为两个实值函数的曲线积分。其它情况下可以用柯西积分公式。如果积分路径是闭合的，并且积分函数在区域中是解析的且没有奇点，那么它的曲线积分是零，这是柯西积分定理的推论。根据留数定理，可以用复平面上的围道积分计算实值函数在实区间上的积分。

例子

考虑复函数 $f(z)={\frac {1}{z}}$ ，设积分路径 $L$ 为单位圆（模长为1的复数的集合）。我们使用 $\gamma (t)=e^{it}$ 来将路径参数化，其中 $t$ 在 $[0,2\pi ]$ 内。代入积分式就得到：

${\begin{aligned}\oint _{L}f(z)\,\mathrm {d} z&=\int _{0}^{2\pi }{1 \over e^{it}}ie^{it}\,\mathrm {d} t=i\int _{0}^{2\pi }e^{-it}e^{it}\,\mathrm {d} t\\&=i\int _{0}^{2\pi }\,\mathrm {d} t=i(2\pi -0)=2\pi i.\end{aligned}}$

用柯西积分定理也可以得到结果。

量子力学

量子力学中的“曲线积分形式”和曲线积分并不相同，因为曲线积分形式中所用的积分是函数空间上的泛函积分，即关于空间中每个路径的概率函数进行积分。然而，曲线积分在量子力学中仍有重要作用，比如说复围道积分常常用来计算量子散射理论中的概率振幅。

参看

费曼－卡茨公式
传播子，费恩曼传播子使用复平面的曲线积分
留数定理，使用复平面的曲线积分

注释

分为曲线积分（或）或路徑積分（或contour integral，参考留数定理
路径积分中当积分路径为闭合曲线时，又称为环路积分或围道积分。

参考文献

Ahlfors, Lars. . : 103.

外部链接

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] 分为曲线积分（或）或路徑積分（或contour integral，参考留数定理

[2] 路径积分中当积分路径为闭合曲线时，又称为环路积分或围道积分。

[3] Ahlfors, Lars. . : 103.