X
步骤
方法 1
方法 1 的 3:
使用长和宽
-
将长和宽代入到公式中。长和宽应该是已知条件,又或者你可以量出它们的长度。确保你用长和宽代入的是和。
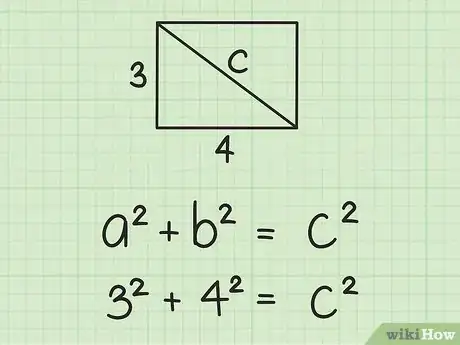
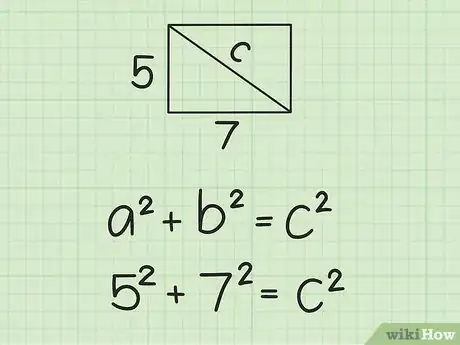
- 例如,如果矩形的宽是3 cm,而长是4 cm,代入公式后得到如下等式:。
-
算出长和宽的平方,然后相加求和。记住,一个数的平方等于用这个数乘以自己。
- 例如:
- 例如:
-
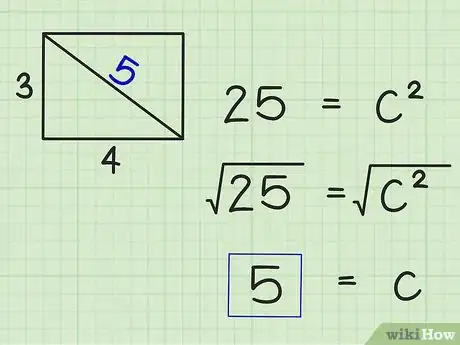
将等式两边开平方。最简单的计算平方根的方法是使用计算器。如果你没有科学计算器,可以使用在线计算器。[5] 这样可以算出的值,即三角形的斜边,也就是矩形对角线的长度。
- 例如:
因此,宽为3 cm,而长为4 cm的矩形,其对角线的长度是5 cm。
广告 - 例如:
方法 2
方法 2 的 3:
使用面积和周长
-
将矩形的面积代入到公式中。确保你代入的是变量。
- 例如,如果矩形的面积是35平方厘米,则代入后得到如下等式:。
-
变换等式,使之变成的表达式。等式两边都除以。将这个表达式放到一边。稍后你会将它代入周长公式。
- 例如:
。
- 例如:
-
将周长的值代入到公式中。确保你代入的是变量。
- 例如,如果矩形的周长是24厘米,则代入后会得到如下等式:。
-
等式两边都除以2。这样就算出了的值。
- 例如:
。
- 例如:
-
将的表达式代入到等式中。使用你变换面积公式得到的表达式。
- 例如,如果使用你变换而得的表达式,把它代入周长公式中的:
- 例如,如果使用你变换而得的表达式,把它代入周长公式中的:
-
去掉等式中的分母。等式两边都乘以。
- 例如:
- 例如:
-
使等式一边等于0。等式两边都减去一次项。
- 例如:
- 例如:
-
按项次对等式重新排序。这意味着带指数的项排第一个,然后是带变量的项,最后是常量。重新排序时,请注意保留正确的正、负符号。你应该注意到了,这个等式现在变成了一个二次方程。
- 例如,变成了。
-
将二次方程因式分解。关于如何进行此步骤的完整说明,请阅读解二次方程。
- 例如,方程可因式分解成。
-
求的值。令各项等于零,求出变量。你会得到方程的两个解,或两个根。由于你面对的是一个矩形,所以得到的两个根是矩形的宽和长。
- 例如:
及
。
因此,矩形的长和宽分别为7 cm和5 cm。
- 例如:
-
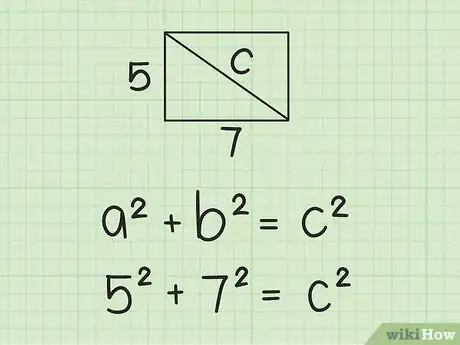
将宽和长代入到公式中。此时,长可以随意代入到a或b中,将宽代入另一个即可。
- 例如,如果你算出矩形的宽和长为5 cm和7 cm,代入后得到如下等式:。
-
算出宽和长的平方,然后相加求和。记住,一个数的平方等于用这个数乘以自己。
- 例如:
- 例如:
-
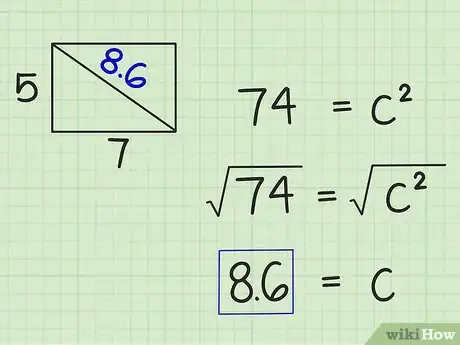
将等式两边开平方。最简单的计算平方根的方法是使用计算器。如果你没有科学计算器,可以使用在线计算器。[10] 这样可以算出的值,即三角形的斜边,也就是矩形对角线的长度。
- 例如:
因此,面积为而周长为24 cm的矩形,其对角线长度约等于8.6 cm。
广告 - 例如:
方法 3
方法 3 的 3:
使用面积和边长的相对关系
-
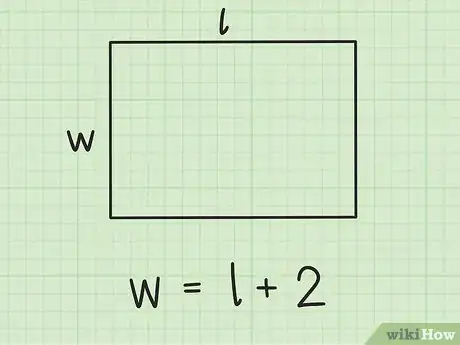
写下能够说明两条边边长之间关系的等式。[11] 你可以将之写成长()或宽()的表达式。将这个等式放到一边。稍后你会将它代入面积公式。
- 例如,如果已知矩形的宽比矩形的长要长2 cm,你可以列出的表达式:。
-
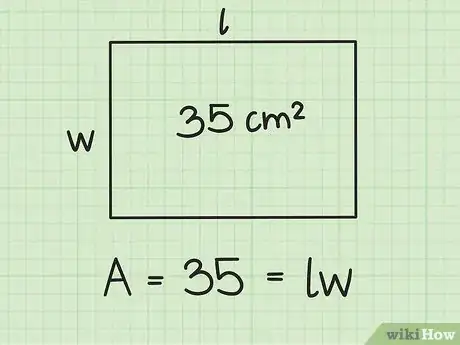
将矩形的面积代入到公式中。确保你代入的是变量。
- 例如,如果矩形的面积是35平方厘米,则代入后得到如下等式:。
-
将长或宽的关系表达式代入公式中。由于你面对的是一个矩形,所以求或变量的值都可以。
- 例如,如果你知道,可以将这个表达式代入面积公式中的:
- 例如,如果你知道,可以将这个表达式代入面积公式中的:
-
列出二次方程。用括号前的系数乘以括号内的各项,然后使方程的一边等于0。
- 例如:
- 例如:
-
将二次方程因式分解。关于如何进行此步骤的完整说明,请阅读解二次方程。
- 例如,方程可因式分解成。
-
求的值。令各项等于零,求出变量。你会求出方程的两个解,或两个根。
- 例如:
及
。
在本例中,你会得到一个负数根。由于矩形的长不可能为负数,所以长必定为5 cm。
- 例如:
-
将长或宽的值代入到关系表达式中。这样就算出了矩形另一条边的边长。
- 例如,如果你知道矩形的长为5 cm, 且边长之间的关系为,可以将长的值5代入到表达式中:
- 例如,如果你知道矩形的长为5 cm, 且边长之间的关系为,可以将长的值5代入到表达式中:
-
将宽和长代入到公式中。此时,长可以随意代入到a或b中,将宽代入另一个即可。
- 例如,如果你算出矩形的宽和长为5 cm和7 cm,代入后得到如下等式:。
-
算出宽和长的平方,然后相加求和。记住,一个数的平方等于用这个数乘以自己。
- 例如:
- 例如:
-
将等式两边开平方。最简单的计算平方根的方法是使用计算器。如果你没有科学计算器,可以使用在线计算器。[16] 这样可以算出的值,即三角形的斜边,也就是矩形对角线的长度。
- 例如:
因此,宽比长要长2 cm,且面积为的矩形,其对角线的长度约等于8.6 cm。
广告 - 例如:
参考
- ↑ http://www.mathopenref.com/rectanglediagonals.html
- ↑ http://www.mathwarehouse.com/geometry/quadrilaterals/parallelograms/rectangle.php
- ↑ http://mathworld.wolfram.com/PythagoreanTheorem.html
- ↑ http://www.mathopenref.com/rectanglediagonals.html
- ↑ https://support.google.com/websearch/answer/3284611?hl=en
- ↑ http://www.mathopenref.com/rectanglearea.html
- ↑ http://www.mathopenref.com/rectangleperimeter.html
- ↑ http://mathworld.wolfram.com/PythagoreanTheorem.html
- ↑ http://www.mathopenref.com/rectanglediagonals.html
- ↑ https://support.google.com/websearch/answer/3284611?hl=en
- ↑ http://www.algebralab.org/Word/Word.aspx?file=Geometry_AreaPerimeterRectangles.xml
- ↑ http://www.mathopenref.com/rectanglearea.html
- ↑ http://www.mathopenref.com/rectangleperimeter.html
- ↑ http://mathworld.wolfram.com/PythagoreanTheorem.html
- ↑ http://www.mathopenref.com/rectanglediagonals.html
- ↑ https://support.google.com/websearch/answer/3284611?hl=en
关于本wikiHow
广告
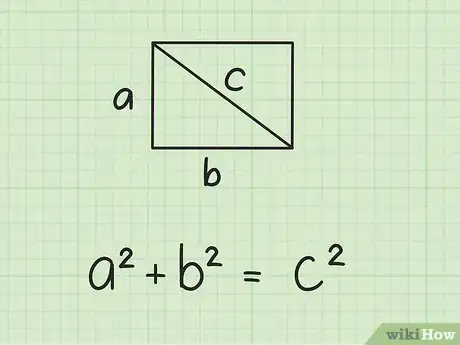





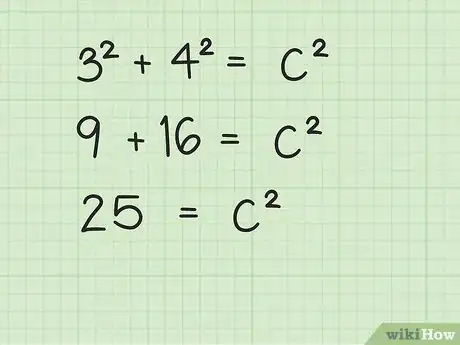













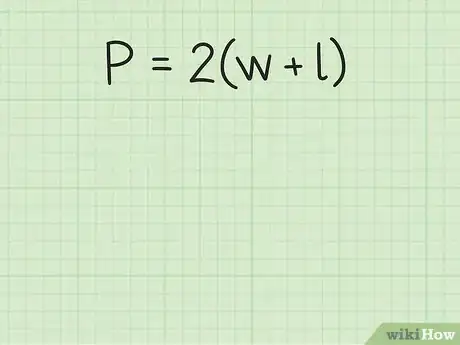

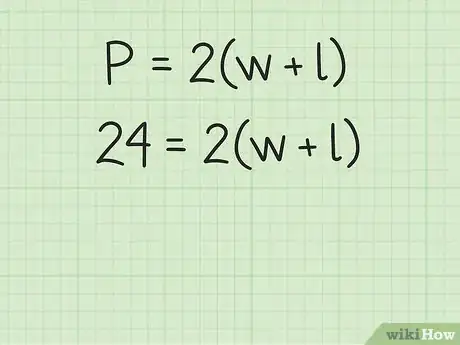


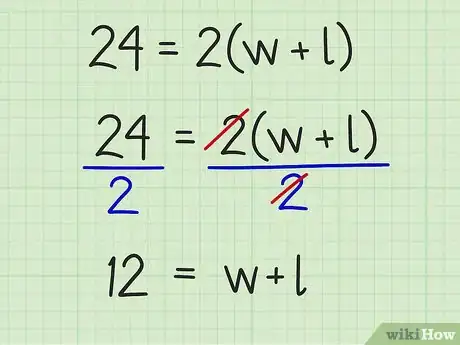



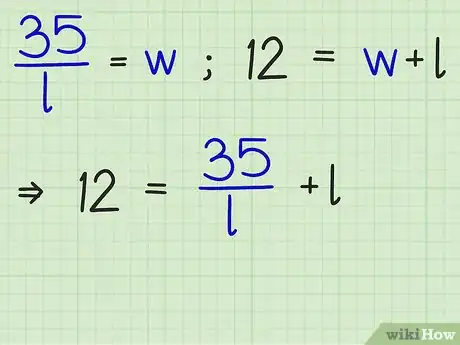

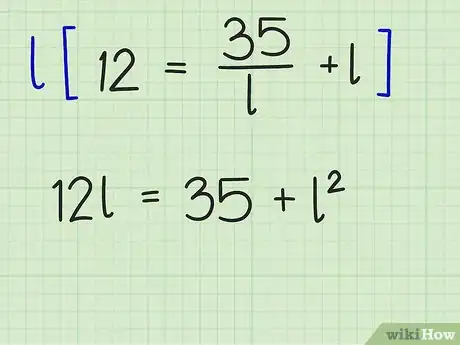







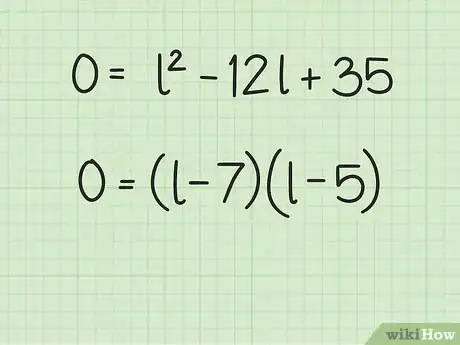






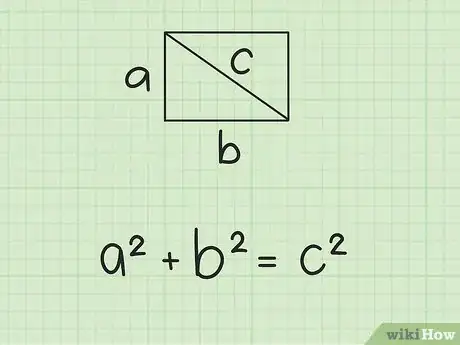

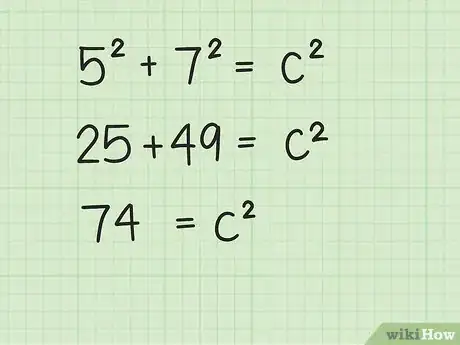






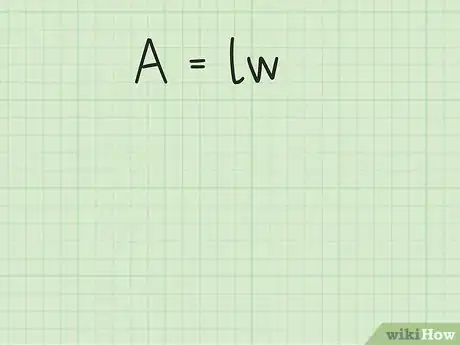
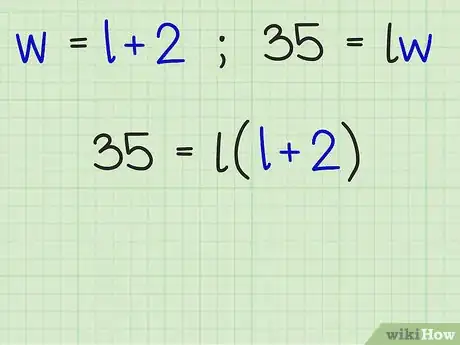

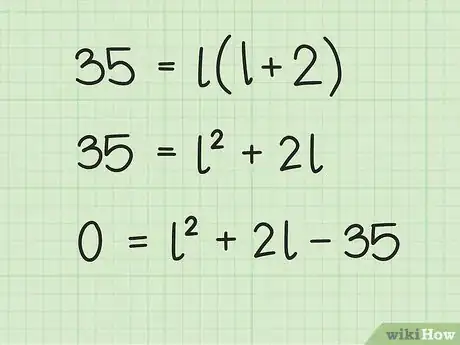


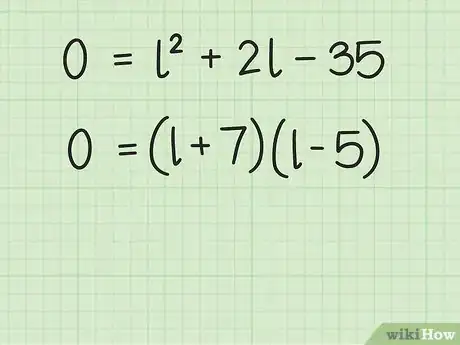







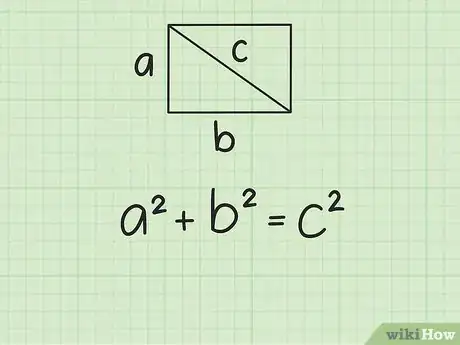
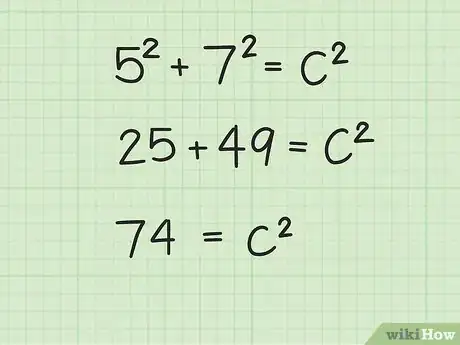









wikiHow的内容管理团队会严密监督编辑人员的工作,确保每篇文章都符合我们的高质量标准要求。 这篇文章已经被读过36,969次。