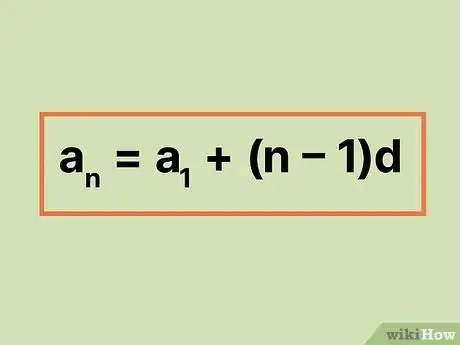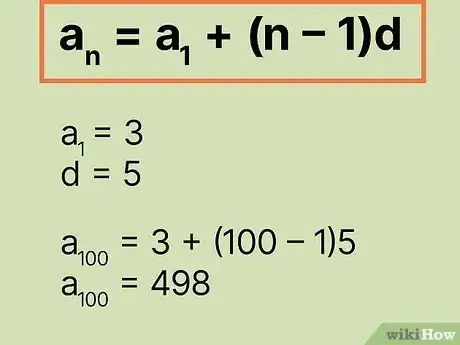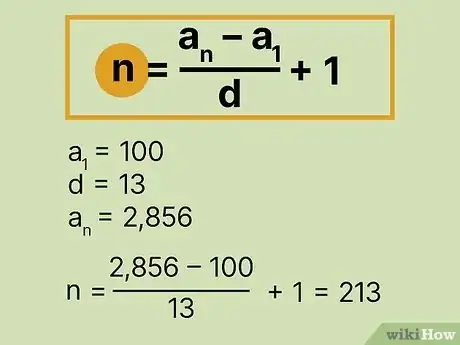如何求等差数列的任意项

共同创作者是 Joseph Meyer

等差数列是每一项与它前面一项的差等于一个常数的数列。例如，偶数列 $0,2,4,6,8$ …就是一个等差数列，因为数列中的数字和下一个数字的差总是等于2。^{[1]
X
研究来源}如果题目中的数列是等差数列，那么你可能需要求出几个已知数字的下一项。题目还可能要你填入等差数列中缺少的那一项。最后，你可能还需要在不写出所有100项的情况下，求出第100项的值。无论题目是哪种类型，只需几个简单步骤，你就能算出答案。

方法 1

方法 1 的 4:

求等差数列的下一项

1
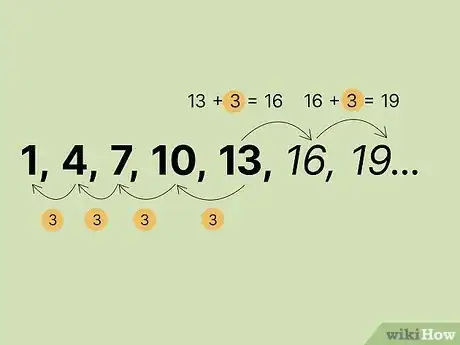
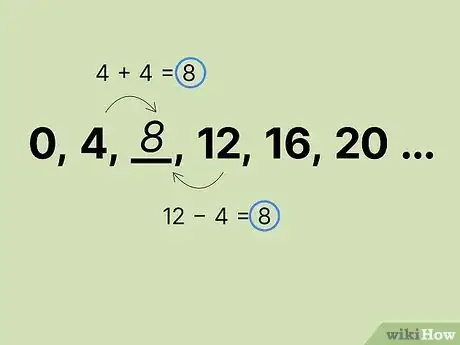
求得数列的公差。面对一组数字时，有时题目会告诉你它们是等差数列，而有时你必须自己认识到这一点。无论是哪种情况，第一步都是相同的。从几个数字中选择最开始的两项。用第二项减去第一项。所得结果就是数列的公差。^{[2]
X
研究来源}
- 例如，假设有一组数字 $1,4,7,10,13$ …。用 $4-1$ ，求得公差为3。
- 假设有一列各项不断变小的数字，如 $25,21,17,13$ …。还是用第二项减去第一项来求出公差。这种情况下， $21-25=-4$ 。负数结果说明从左到右看时，这组数字在逐渐变小。每次做题时，你都应该检查公差的正负号，看是否与数字的变化趋势相符。
2
检查公差是否一致。只计算前两项的公差，不足以保证数列是等差数列。你需要确保整列数字的差值始终一致。^{[3]
X
研究来源}。将数列中另外两个连续项相减，检查它们的差值。如果结果与另外一到两次的结果一致，那么它就很可能是等差数列。
- 还是以数列 $1,4,7,10,13$ …为例，选择数列的第二项和第三项。用 $7-4$ ，差值仍然为3。保险起见，再选两个连续项相减， $13-10$ ，差值为3，还是与之前的结果相吻合。现在，你可以比较确定它是一组等差数列了。
- 有时，数列的前几项看上去像等差数列，但之后却不符合等差数列的特征。例如，数列 $1,2,3,6,9$ …。第一项和第二项之间的差是1，而第二项和第三项之间的差也是1。但是，第三项和第四项之间的差是3。由于数列各项之差并不相等，所以它不是等差数列。
3
用公差加上最后的已知项。知道公差后，求等差数列的下一项就非常简单了。只需用公差加上最后的已知项，就可以得出下一个数字。
- 例如，在示例 $1,4,7,10,13$ …中，要算出下一个数字，你可以用公差3加上最后的已知项。 $13+3$ 等于16，16就是下一个数字。只要愿意，你可以不断加3，写出数列后面的数字。例如，将数列后面的数字写出来后，我们得到 $1,4,7,10,13,16,19,22,25$ …。你可以一直写下去，直到满意为止。
广告

方法 2

方法 2 的 4:

求缺少的中间项

1
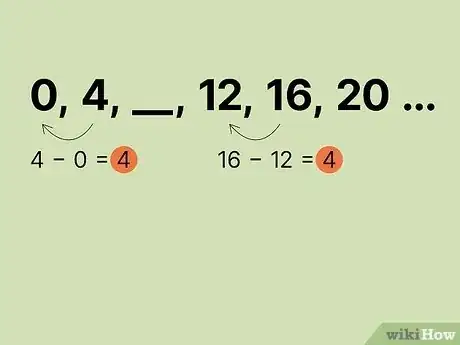
首先检查是否是等差数列。某些情况下，题目会给出一组缺少中间项的数字。和之前一样，首先你应该检查数列是否是等差数列。选择任意的连续两项数字，计算它们之间的差值。比较结果与数列中另外两个连续数字的差值。如果差值相等，那么你可以假设自己面对的是一个等差数列，然后继续使用本文的等差数列方法。
- 例如，假设有一个数列 $0,4$ ,___, $12,16,20$ …。先用 $4-0$ ，求得差值为4。比较另外两个连续数字的差，如 $16-12$ 。差值仍等于4。因此，你可以将之当做等差数列，继续解题。
2
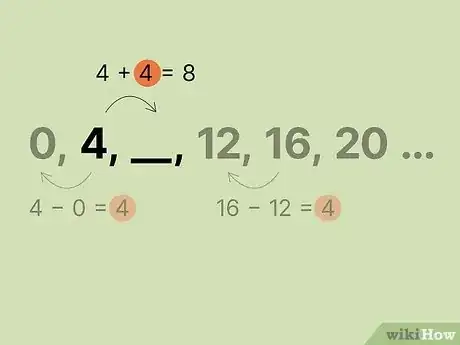
用公差加上空格前的那一项。方法和求数列最后一项类似。找到数列中空格前的那一项。这是已知的“最后一个”数字。用公差加上该项，算出应该填入空格的数字。^{[4]
X
研究来源}
- 在当前示例中， $0,4$ ,____, $12,16,20$ …，空格前的数字是4，而此数列的公差也是4。所以，用 $4+4$ ，得到8，它应该就是空格中的数字。
3
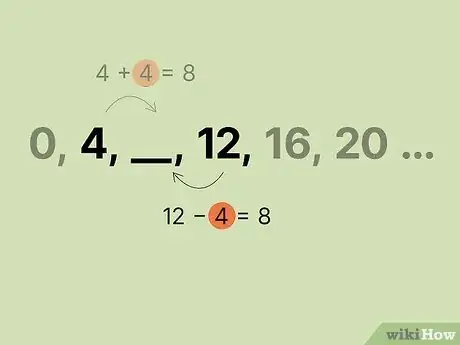
用空格后的数字减去公差。为了确保答案正确，可以从另一个方向来进行检查。无论是正序还是倒序，等差数列应该都符合自身特点。如果从左到右需要逐项加4，那么反过来，从右到左就正好相反，需要逐项减4。
- 在当前示例中， $0,4$ ,___, $12,16,20$ …，空格后的数字是12。用该项减去公差，得到 $12-4=8$ 。你应该将结果8填入空格中。
4
比较结果。用左边项加公差和用右边项减公差算出来的两个结果应该相等。如果相等，说明你已经求得缺少项的值。如果不相等，则说明你需要检查自己的计算过程。题目中的数列可能并非等差数列。
- 在当前示例中， $4+4$ 和 $12-4$ 算得的结果都是8。因此，该等差数列的缺少项为8。完整的数列是 $0,4,8,12,16,20$ …。
广告

方法 3

方法 3 的 4:

求等差数列的第N项

1
确定数列的第一项。并非所有序列都以数字0或数字1开始。查看题中的数列，找到第一项。它是计算的起点，可以使用变量a(1)代表。
- 面对等差数列问题时，经常会使用变量a(1)来指代数列的第一项。当然，你可以选择自己喜欢的任何变量，这并不会影响到结果。
- 例如，已知数列 $3,8,13,18$ …，第一项是 $3$ ，我们可以用a(1)来指代。
用上文所述方法求出数列的公差。在当前示例中，公差等于 $8-3$ ，等于5。使用数列中的其他数字进行检查，得到同样的结果。我们用变量d来指代该公差。^{[5]
X
研究来源}
3
使用显式公式。显式公式是一个代数方程，使用它来求等差数列的任意项时，你无须写出完整数列。等差数列的显式公式为 $a(n)=a(1)+(n-1)d$ $a(n)=a(1)+(n-1)d$ 。
- a(n)项可以读作“a的第n项”，其中n代表数列中你想求出的项数，而a(n)是该项的实际数值。例如，如果题目要求你求等差数列的第100项，那么n等于100。注意，在本示例中，n等于100，但a(n)等于第100项的值，而不等于数字100本身。
4
填入已知信息解题。使用数列的显式公式，填入已知信息，求出需要的项。
- 例如，在本示例中， $3,8,13,18$ …，我们知道a(1)是第一项，等于3，而公差d等于5。假设题目要求你求出数列的第100项，则n=100，而(n-1)=99。填入数值后，完成显式公式，得到 $a(100)=3+(99)(5)$ 。简化后的结果是498，这个数字就是该数列的第100项。
广告

方法 4

方法 4 的 4:

使用显式公式求其他数值

1
对显式公式进行变形，求其他变量。使用显式公式和基础的代数知识，你可以算出等差数列的几个其他数值。显式公式的初始形式是 $a(n)=a(1)+(n-1)d$ $a(n)=a(1)+(n-1)d$ ，其目的是求a_n，也就是数列的第n项。但是，你可以对公式进行代数变形，来计算任何其他变量。
- 例如，假设数列的最后一个数字已知，需要你计算数列最开始的数字。你可以将公式变形，得到 $a(1)=(n-1)d-a(n)$ 。
- 如果你知道等差数列的第一个数字和最后一个数字，但需要算出该数列的项数，你可以将显式公式变形来求出n。公式变形后可得 $n={\frac {a(n)-a(1)}{d}}+1$ 。
- 如果为了将公式变形，你需要复习基础的代数知识，可以参阅本网站的学习代数或化简代数表达式相关文章。
2
求数列的第一项。已知等差数列的第50项为300，且每项比之前一项大7，即“公差”等于7，求序列第一项的值。使用变形后的显式公式来计算a1，求得问题的答案。
- 使用方程 $a(1)=(n-1)d-a(n)$ ，然后代入已知信息。由于已知第50项为300，所以n=50，n-1=49，且a(n)=300。题目还提供了公差d的值，d等于7。因此，公式变为 $a(1)=(49)(7)-300$ 。得到 $343-300=43$ 。数列的第一项是43，每一项比前一项大7。因此，数列可以写作 43,50,57,64,71,78…293,300。
3
求数列的项数。假设你只知道等差数列的第一项和最后一项，需要求数列的项数。使用变形后的公式 $n={\frac {a(n)-a(1)}{d}}+1$ $n={\frac {a(n)-a(1)}{d}}+1$ 。
- 假设已知等差数列的第一项是100，公差为13。题目还告知最后一项是2,856。要计算数列的项数，可以用到的信息有a1=100，d=13，以及a(n)=2856。将这些值代入公式，得到 $n={\frac {2856-100}{13}}+1$ 。计算后，可得 $n={\frac {2756}{13}}+1$ ，等于212+1，即213。所以该序列有213项。
- 该序列可以写作100, 113, 126, 139… 2843, 2856。
广告