X
这篇文章由我们训练有素的编辑和研究团队共同创作,他们对文章的准确性和全面性进行了验证。
wikiHow的内容管理团队会严密监督编辑人员的工作,确保每篇文章都符合我们的高质量标准要求。
这篇文章已经被读过242,909次。
三次方程的最高次数为3次,它有3个解,或者说3个根,方程本身的形式是。虽然三次方程有些令人望而生畏,并且的确不好解,但在具备大量基础知识的前提下,只要使用正确的方法,即使是最棘手的三次方程问题也可以顺利求解。三次方程的解法有很多种,你可以尝试使用二次公式、求整数解或确定判别式方法。
步骤
方法 1
方法 1 的 3:
解不含常数项的三次方程
-
提取方程的公因式。由于方程没有常数项,所以其中各项都包含变量。也就是说,可以提取方程的公因式来简化方程。这样做之后,可以将方程重写为。[3]
- 例如,假设我们一开始要解的方程是。
- 提取方程的公因式,得到。
-
如果无法手动对括号内的部分进行因式分解,可使用二次公式求解。你可以将、、的值代入二次公式()中,算出使二次方程等于0的x值。使用这种方法可以求出三次方程的两个解。[5]
- 示例中,将、和的值、和分别代入到以下二次公式:
- 解1:
- 解2:
- 示例中,将、和的值、和分别代入到以下二次公式:
-
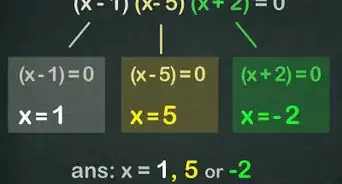
零和二次方程的解就是三次方程的解。二次方程有两个解,而三次方程有三个。你已经求出其中的两个解,即你为括号中“二次”部分求出的解。对于可以用“因式分解”方法求解的方程,第三个解一定为。[6]
- 将方程分解为包含两个因式的形式,左边的因式是变量,右边的因式是括号内的二次方程。如果任一因式等于,则整个方程等于。
- 因此,使括号内的二次因式等于的两个解是三次方程的解,而使左边因式等于的本身,也是三次方程的解。
广告
方法 2
方法 2 的 3:
使用因数表求整数解
-
确保三次方程有一个值不等于零的常数项。如果形式为的方程拥有一个不等于零的值,那就无法将它因式分解为二次方程。但是不用担心,你还可以使用其他方法,比如下文中介绍的方法。[7]
- 以方程为例。这个方程中,要让等号的右边等于,你需要两边都加。
- 得到新的方程。由于,你无法使用二次方程方法。
-
找出和的因数。要解三次方程,我们需要先关注项的系数以及方程最后的常数项,找出它们各自的因数。记住,如果两个数字相乘得到另一个数,那么这两个数就是乘积的因数。[8]
- 例如,由于你可以用和得到6,所以1、2、3、6就是6的因数。
- 例题中,,而。2的因数是1和2。6的因数是1、2、3、6。
-
用的因数除以的因数。将的各因数除以的各因数所得的值罗列出来。这样做通常会得到许多分数和几个整数。三次方程的整数解要么是其中的一个整数,要么是其中一个整数的相反数。[9]
- 例题中,用的因数1和2除以的因数1、2、3、6,得到:,,,,和。然后,我们将各数字的相反数加入进去,使之更加完整:,,,,,,,,,,和。三次方程的整数解就在其中。
-
手动代入整数,这种方法较为简单,但可能会比较费时。得到相除的结果后,你可以迅速将整数手动代入,看哪些能让三次方程等于,进而求出方程的解。例如,如果将代入方程,可以得到:[10]
- ,即,结果不等于。因此,使用得到的下一个值。
- 如果将代入方程,得到,结果等于。这意味着是方程的一个整数解。
-
使用更复杂,但可能更快速的综合除法。如果你不想花时间一个一个地去代入所有的值,不妨尝试一下更快捷的方法,也就是所谓的综合除法。总的来说,你应该使用综合除法,用得到的整数值除以、、和。如果得到余数,那么这个值就是三次方程的解。[11]
- 综合除法是一个复杂的主题,超出了本文论述的范围。以下的例子示范了如何用综合除法求三次方程的解:
- -1 | 2 9 13 6
- __| -2-7-6
- __| 2 7 6 0
- 由于得到的最终余数为,由此可知,是三次方程的一个整数解。
广告 - 综合除法是一个复杂的主题,超出了本文论述的范围。以下的例子示范了如何用综合除法求三次方程的解:
方法 3
方法 3 的 3:
使用判别式方法
-
使用正确的公式计算判别式零。用判别式方法求三次方程的解会用到十分复杂的数学原理,但如果严格遵循方法流程,你会发现,它在解令其他方法束手无策的三次方程方面十分实用。首先,将适当的值代入到公式中,求出第一个重要数值,即判别式零。[13]
- 判别式是一个数字,可以为我们提供关于多项式根的信息。你可能已经知道二次判别式是()。
- 例题中的计算过程如下:
-
计算: 。然后,我们会使用和的值计算三次方程的判别式。在三次方程中,如果判别式为正数,则方程有三个实数解。如果判别式等于零,则方程有一个或两个实数解,且有时两个实数解会相等。如果判别式为负数,则方程只有一个实数解。[15]
- 三次方程必定有至少一个实数解,因为其函数图形必定会与X轴相交至少一次。
- 例题中,由于和都等于,所以的计算相对简单。计算过程如下:
- ,所以方程有一个或两个解。
-
计算: 。最后一个需要计算的重要数值是。它能帮助我们在最后求出三个根。按照正常计算过程,根据需要代入 和。
- 例题中,的计算过程如下:
- 例题中,的计算过程如下:
-
使用变量计算三个根。三次方程的根或解可以使用公式计算,其中,而n等于1、2或3。根据需要代入数值进行计算,其中涉及到大量的数学运算,但你应该可以得到三个使方程成立的解。
- 你可以分别计算n等于1、2、3时公式的值,来求得例题的答案。这样得到的答案可能就是三次方程的解。你可以将答案代入到方程中,使之等于0的答案即为方程的正确解。
- 例如,将1代入到中,计算结果为0,所以1就是三次方程的一个解。
广告
参考
- ↑ http://www.mathcentre.ac.uk/resources/uploaded/mc-ty-cubicequations-2009-1.pdf
- ↑ https://sciencing.com/solve-cubic-equations-8136094.html
- ↑ https://sciencing.com/solve-cubic-equations-8136094.html
- ↑ http://www.mathcentre.ac.uk/resources/uploaded/mc-ty-cubicequations-2009-1.pdf
- ↑ https://www.purplemath.com/modules/quadform.htm
- ↑ https://math.vanderbilt.edu/schectex/courses/cubic/
- ↑ http://www.rasmus.is/uk/t/F/Su52k02.htm
- ↑ http://www.rasmus.is/uk/t/F/Su52k02.htm
- ↑ http://www.rasmus.is/uk/t/F/Su52k02.htm
- ↑ http://www.rasmus.is/uk/t/F/Su52k02.htm
- ↑ http://www.rasmus.is/uk/t/F/Su52k02.htm
- ↑ http://www2.trinity.unimelb.edu.au/~rbroekst/MathX/Cubic%20Formula.pdf
- ↑ http://www2.trinity.unimelb.edu.au/~rbroekst/MathX/Cubic%20Formula.pdf
- ↑ http://www2.trinity.unimelb.edu.au/~rbroekst/MathX/Cubic%20Formula.pdf
- ↑ http://www2.trinity.unimelb.edu.au/~rbroekst/MathX/Cubic%20Formula.pdf
关于本wikiHow
广告

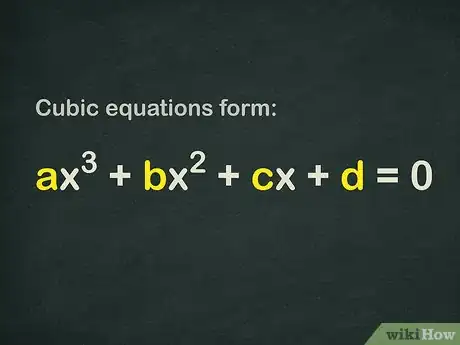



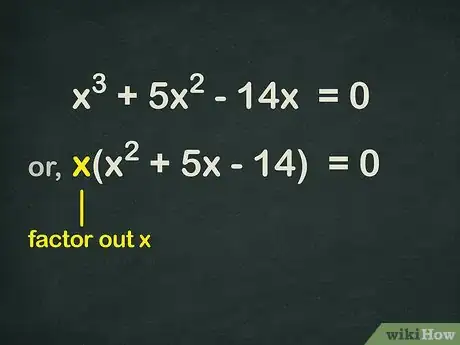




























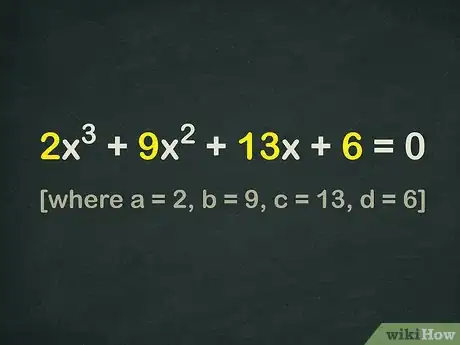




















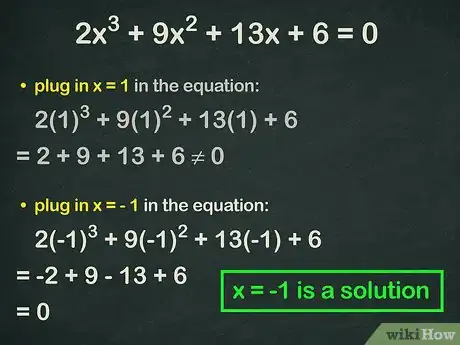




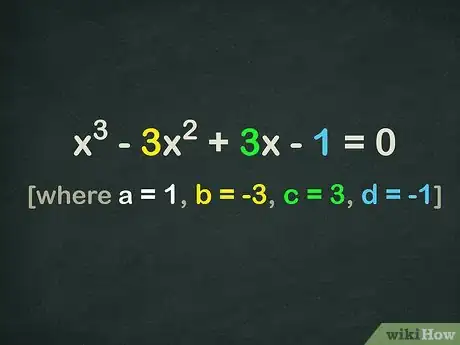





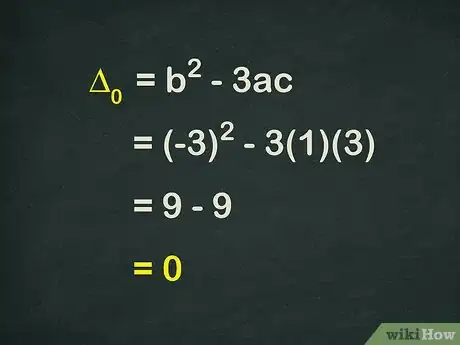






















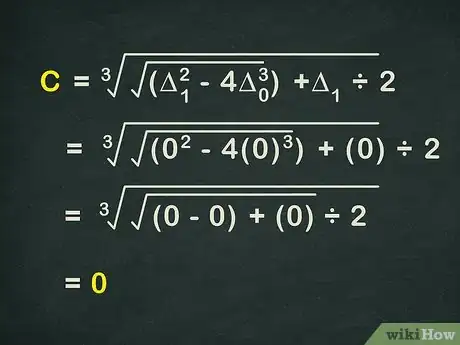






































wikiHow的内容管理团队会严密监督编辑人员的工作,确保每篇文章都符合我们的高质量标准要求。 这篇文章已经被读过242,909次。