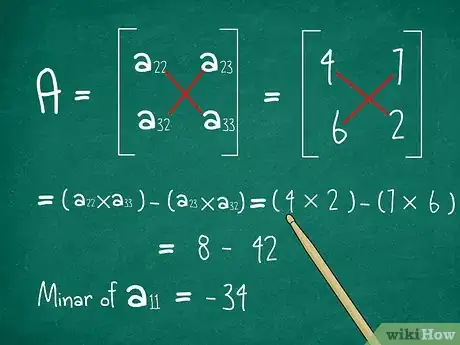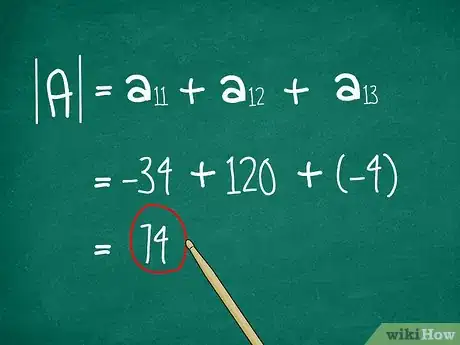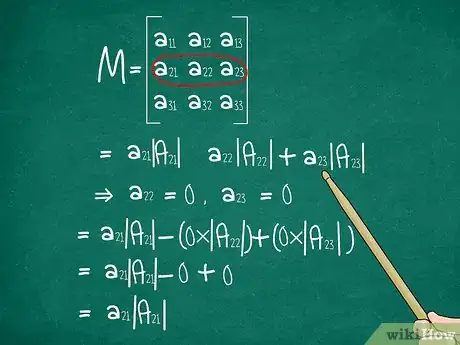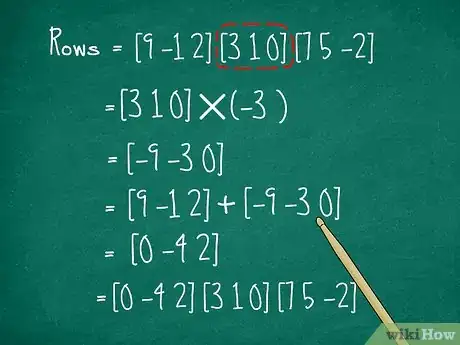如何求3X3矩阵的行列式

作者信息

参考

矩阵的行列式常用于微积分、线性代数和高等几何。求一个矩阵的行列式一开始可能会让人困惑，但只要做过几次后，你就会觉得并不是那么难。

部分 1

部分 1 的 2:

求行列式

1
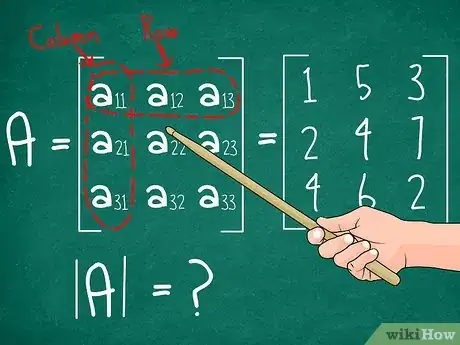
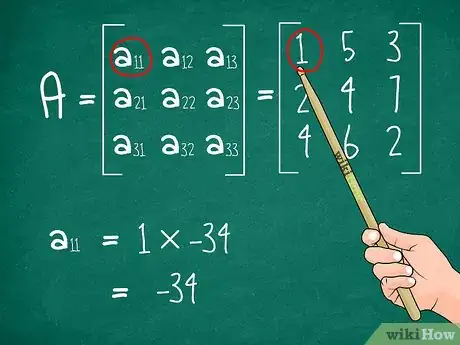
写出3×3矩阵。我们从3x3矩阵A开始，试着找出它的行列式|A|。下面是我们将使用的一般矩阵表示法，以及示例矩阵：^{[1]
X
研究来源}
- $M={\begin{pmatrix}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33}\end{pmatrix}}={\begin{pmatrix}1&5&3\\2&4&7\\4&6&2\end{pmatrix}}$
2
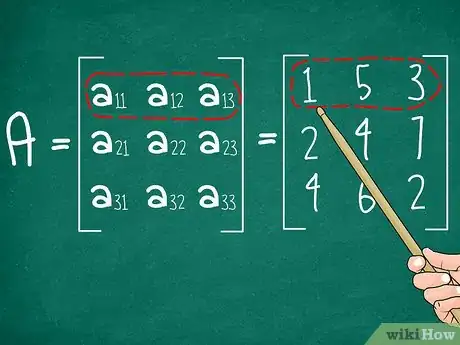
选择单行或单列。这将是引用行或列。不管你选哪一行或列，结果都是一样的。现在，只选择第一行。稍后，我们将给出一些关于如何选择最简单的计算方法的建议。^{[2]
X
研究来源}
- 我们选择示例矩阵A的第一行，圈出1 5 3。一般来说，圈出₁₁ a₁₂ a₁₃。
3
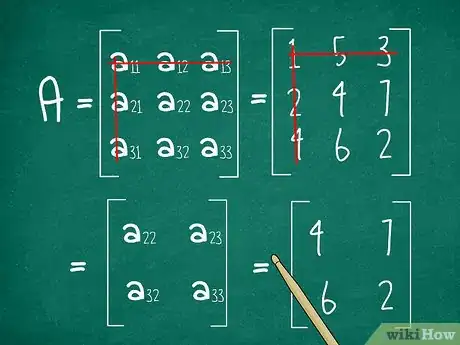
划掉第一个元素的行和列。查看圈出的行或列，并选择第一个元素。通过它的行和列画线。剩下四个数字。我们把它看成一个2×2矩阵。^{[3]
X
研究来源}
- 在本例中，引用行是1 5 3。第一个元素在第1行和第1列。划掉第一行和第一列。把剩下的元素写成2×2矩阵：
- ~~1 5 3~~
  2 4 1
  4 6 2
4
求出2x2矩阵的行列式。记住，这个矩阵 ${\begin{pmatrix}a&b\\c&d\end{pmatrix}}$ ${\begin{pmatrix}a&b\\c&d\end{pmatrix}}$ 有展开式为ad - bc的行列式。你可以通过在2×2矩阵上画一个X来学习这种方法。将X中\连接的两个数字相乘，然后减去/连接的两个数字的乘积。用这个公式计算你刚找出的矩阵的行列式。^{[4]
X
研究来源}
- 在本例中，矩阵的行列式为 ${\begin{pmatrix}4&7\\6&2\end{pmatrix}}$ = 4 * 2 - 7 * 6 = -34。
- 这个行列式叫做原始矩阵中所选的元素的余子式。^{[5]
  X
  研究来源}在本例中，我们刚找出了a₁₁的余子式。
5
将结果乘以你选择的元素。记住，当你决定划去哪一行和哪一列时，是从引用行（或列）中选择了一个元素。将这个元素乘以刚刚计算出的2x2矩阵的行列式。^{[6]
X
研究来源}
- 在本例中，我们选择了a₁₁，值为1。将它乘以-34（2x2矩阵的行列式），得到1*-34 = -34。
6
确定答案的正负号。接下来，将答案乘以1或-1来得到所选元素的代数余子式。你用哪一个取决于元素在3x3矩阵中的位置。记住这个简单的正负号图来找出哪个元素是正，哪个元素是负：
- + - +
  - + -
  + - +
- 由于我们选择了a₁₁，用a +标记，将结果乘以1。（也就是说，不用管它）。答案还是-34。
- 或者，你可以用公式(-1)^i+j来计算正负号，其中i和j是该元素的行数和列数。^{[7]
  X
  研究来源}
7
对引用行或列中的第二个元素重复这个过程。返回到初始的3x3矩阵，包含你之前圈出的行或列。对这个元素重复相同的过程：^{[8]
X
研究来源}
- 划掉这个元素所在的行和列。在本例中，选择元素a₁₂（值为5）。划掉第一行（1 5 3）和第二列 ${\begin{pmatrix}5\\4\\6\end{pmatrix}}$ 。
- 将剩余元素当作一个2x2矩阵。在本例中，矩阵为 ${\begin{pmatrix}2&7\\4&2\end{pmatrix}}$
- 求出这个2x2矩阵的行列式。使用ad - bc公式。（2*2 - 7*4 = -24）
- 乘以3x3矩阵中选定的元素。 -24 * 5 = -120
- 确定是否乘以-1。使用正负号表或(-1)^ij公式。我们选择了元素a₁₂，在正负号表中为负。因此要将更改结果的正负号：(-1)*(-120) = 120。
8
对于三个元素重复这个操作。你还要找出一个余子式。计算引用行或列中第三项的i。在本例中，下面是计算a₁₃余子式的简要描述：
- 划掉第1行和第3列，得到 ${\begin{pmatrix}2&4\\4&6\end{pmatrix}}$
- 它的行列式为2*6 - 4*4 = -4。
- 乘以元素a₁₃：-4 * 3 = -12。
- 元素a₁₃在正负号表中为正，所以结果是-12。
9
将三个结果加起来。这是最后一步。你已经算出来三个代数余子式，每个分别对应单行或单列中的每个元素。把它们加起来，你就得到了3x3矩阵的行列式。
- 在本例中，行列式为-34 + 120 + -12 = 74。
广告

部分 2

部分 2 的 2:

简化问题

1
选择0最多的引用行或列。记住，你可以选择任意行或列作为引用。不管你选哪一个，结果都是一样的。如果你选择一个带有零的行或列，只需要计算非零元素的代数余子式。原因如下：^{[9]
X
研究来源}
- 假设你选择第2行，包含元素a₂₁、a₂₂和₂₃。要解决这个问题，我们要看三个不同的2x2矩阵。我们把它们叫做A₂₁、A₂₂和A₂₃。
- 3x3矩阵的行列式是a₂₁|A₂₁| - a₂₂|A₂₂| + a₂₃|A₂₃|。
- 如果a₂₂和a₂₃都为0，公式就变成a₂₁|A₂₁| - 0*|A₂₂| + 0*|A₂₃| = a₂₁|A₂₁| - 0 + 0 = a₂₁|A₂₁|。现在我们只需计算一个元素的代数余子式。
2
利用行加法使矩阵更简单。如果你把一行的值加到另一行，矩阵的行列式不变。列也是如此。你可以重复这样操作，或者在加之前将值乘以一个常数，从而使矩阵有尽可能多的0。这样可以节省很多时间。
- 例如，假设你有一个3×3的矩阵： ${\begin{pmatrix}9&-1&2\\3&1&0\\7&5&-2\end{pmatrix}}$
- 为了消掉a₁₁上的9，我们可以把第二行乘以-3然后把结果加到第一行。新的第一行就变成[9 -1 2] + [-9 -3 0] = [0 -4 2]。
- 新矩阵就变成 ${\begin{pmatrix}0&-4&2\\3&1&0\\7&5&-2\end{pmatrix}}$ 。尝试对列使用同样的方法，将a₁₂也变成0。
3
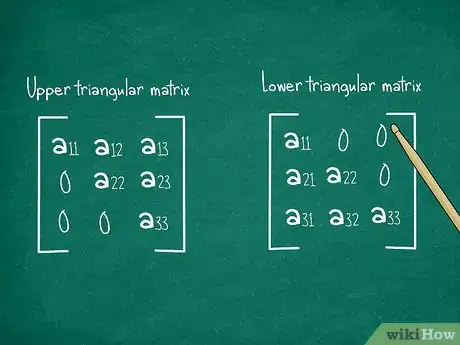
学习三角矩阵的快捷方法。在这些特殊情况下，行列式就是主对角线上的元素的乘积，从左上角的a₁₁到右下角的a₃₃。我们讨论的仍然是3x3矩阵，但是“三角”矩阵有非零值的特殊模式：^{[10]
X
研究来源}
- 上三角矩阵：所有非零元素都在主对角线上或主对角线之上。下面全部是0。
- 下三角矩阵：所有非零元素都在主对角上或主对角之下。
- 对角矩阵：所有非零元素都在主对角上。（上述矩阵的一个子集）
广告