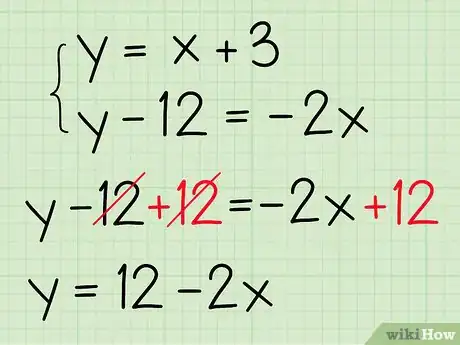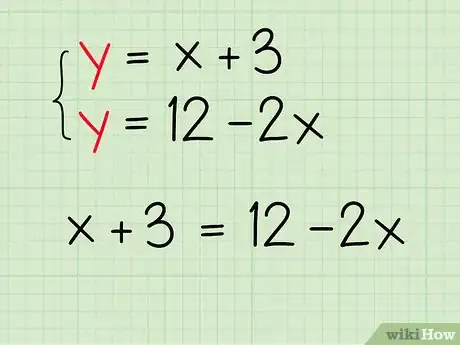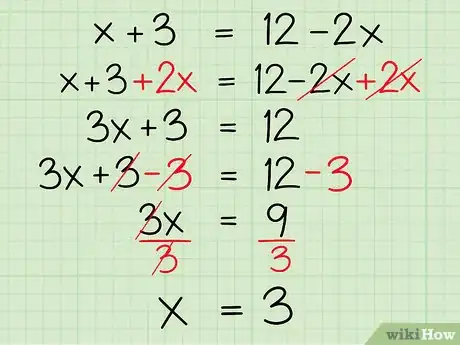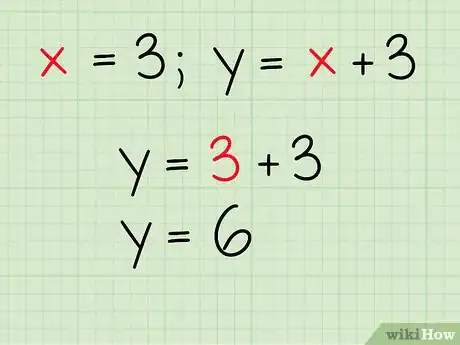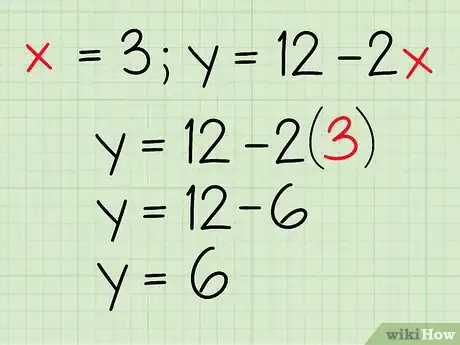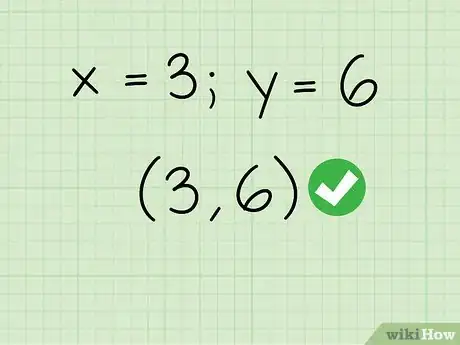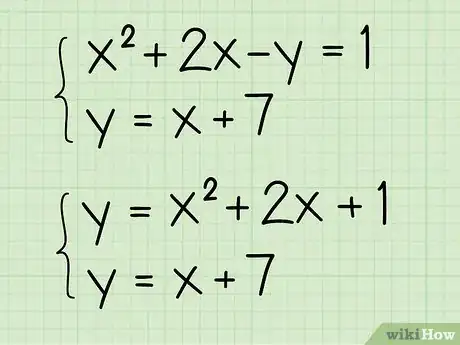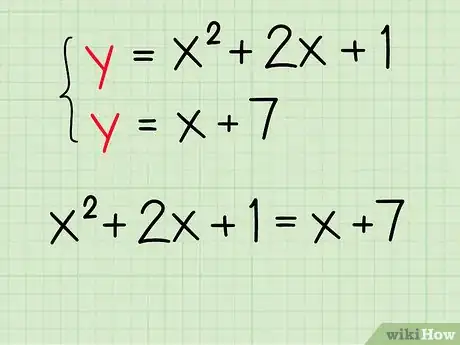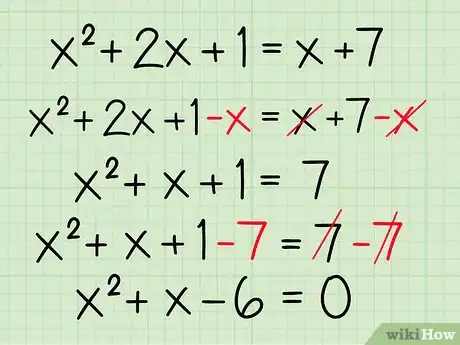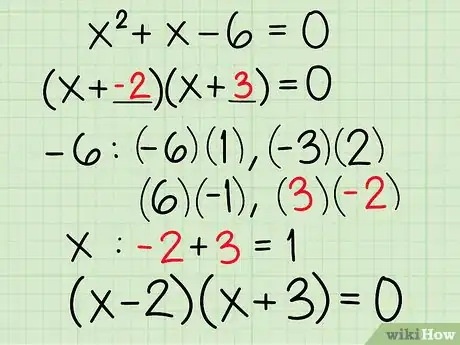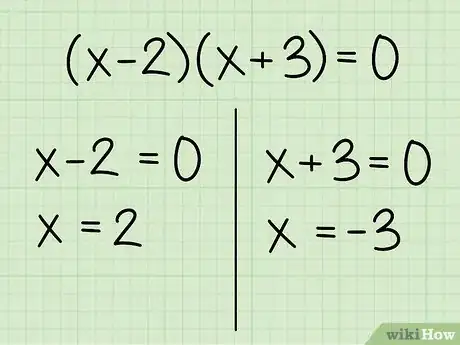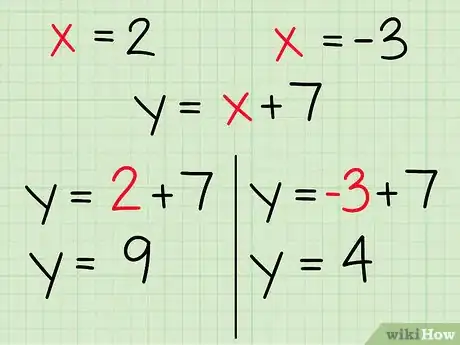如何用代数方法求出两条线的交点

当直线在二维图形上相交时，它们只相交于一点，^{[1]
X
研究来源}由一组坐标 $x$ -和 $y$ -表示。由于两条线都经过那个点，所以 $x$ -和 $y$ - 坐标必须同时满足两个方程。通过一些其他技巧，你就能以此类推，求出抛物线和其他二次曲线的交点。

方法 1

方法 1 的 2:

求两条直线的交点

$Step 1 写出每条直线的方程， y {\displaystyle y} 在等式左侧。$

1
写出每条直线的方程， $y$ 在等式左侧。如果有必要的话，重新排列等式，这样 $y$ $y$ 就单独在等号左侧。如果方程使用 $f(x)$ $f(x)$ 或 $g(x)$ $g(x)$ ，而不是 $y$ $y$ ，那就将这一项单独分开。记住，你可以通过对等式两边执行相同的操作来消除这些项。
- 如果你不会求这个方程，根据现有的信息求出直线方程。
- 例如：两条线分别为： $y=x+3$ 和 $y-12=-2x$ 。要想将第二个方程的 $y$ 分离出来，两边各加上12： $y=12-2x$
2
让两个等式右侧相等。我们在寻找一个点，两条直线在这个点上具有相同的 $x$ $x$ 和 $y$ $y$ 值；这个点就是两条直线相交的位置。两个等式在左侧都是只有 $y$ $y$ ，这样我们就知道两个等式的右侧相等。写出一个新的方程来表示它。
- 例如：已知 $y=x+3$ ， $y=12-2x$ ，所以 $x+3=12-2x$ 。
3
求x。新方程只有一个变量， $x$ $x$ 。用代数来解决这个问题，两边做同样的运算。把 $x$ $x$ 项移到等式的一边，然后将它写成 $x=??$ $x=??$ 的形式。（如果不行，那就跳到这一部分的最后一步。）
- 例如： $x+3=12-2x$
- 两边各加上 $2x$ ：
- $3x+3=12$
- 每边减去3：
- $3x=9$
- 两边各除以3：
- $x=3$
4
用这个 $x$ -值来求解 $y$ 。选择一条直线的方程。将你求出的x值带入这个等式中的所有 $x$ $x$ 。算一下算式，求出 $y$ $y$ 。
- 例如： $x=3$ ， $y=x+3$
- $y=3+3$
- $y=6$
5
检查计算结果。将 $x$ $x$ -值带入另一个方程中来查看是否得到相同的结果，这是一种很好的做法。如果你得到不同的 $y$ $y$ 值，回去检查你的计算过程，检查计算错误。
- 例如： $x=3$ ， $y=12-2x$
- $y=12-2(3)$
- $y=12-6$
- $y=6$
- 两次计算结果一致。没有错误。
6
写出交点的 $x$ 和 $y$ 坐标。现在，你已经求出两条直线交点的 $x$ $x$ -值和 $y$ $y$ -值。将这个交点写成坐标组， $x$ $x$ -值作为第一个值。
- 例如： $x=3$ ， $y=6$
- 这两条直线相交于(3,6)。
7
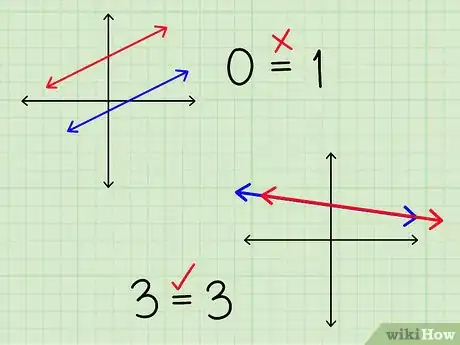
处理异常结果。有些方程是不可能解出来 $x$ $x$ 的。这不一定是你出错了。两条直线有两种方式会导致出现特殊结果：
- 如果两条直线平行，它们不相交。 $x$ 项就会抵消，方程就会简化成错误的表述（例如 $0=1$ ）。可以写出“这两条直线不相交”或“没有实数解”作为答案。
- 如果两个方程描述的是同一条直线，直线上的所有点都“相交”。 $x$ 项抵消，方程就会简化成一个正确的表述（例如 $3=3$ ）。可以写出“这两条直线是同一条”作为答案。
广告

方法 2

方法 2 的 2:

二次方程问题

1
识别二次方程。在二次方程中，一个或多个变量的高次数是2（ $x^{2}$ $x^{2}$ 或 $y^{2}$ $y^{2}$ ），没有更高的次数。这些方程表示是曲线，所以它们和直线的交点数量可以是0、1或2。本部分将教你如何求出0、1或2个交点。
- 用展开方程的括号，检查它是否是二次方程。例如， $y=(x+3)(x)$ 是二次方程，因为它可以展开为 $y=x^{2}+3x$
- 圆或椭圆的方程都有 $x^{2}$ 和 $y^{2}$ 项。^{[2]
  X
  研究来源}^{[3]
  X
  研究来源}如果你在处理这些特殊情况时遇到困难，请参阅下面的“小技巧”部分。
2
把方程写成y的形式。如果有必要的话，把每个方程重写一下，使y单独在等式的一边。
- 例如：求出 $x^{2}+2x-y=-1$ 和 $y=x+7$ 的交点。
- 用y表示二次方程：
- $y=x^{2}+2x+1$ 和 $y=x+7$ 。
- 本例中有一个二次方程和一个线性方程。两个二次方程的问题可以用类似的方法求解。
3
结合两个方程来消去y，两个方程左侧都为y时，你就知道两个方程的右侧是相等的。
- 例如： $y=x^{2}+2x+1$ ， $y=x+7$
- $x^{2}+2x+1=x+7$
4
把新方程整理一下，让一边等于0。使用标准的代数方法把所有的项都移到一边。这样问题就解决了，我们可以在下一步中解决这个问题。
- 例如： $x^{2}+2x+1=x+7$
- 两边同时减去x：
- $x^{2}+x+1=7$
- 两边同时减去7：
- $x^{2}+x-6=0$
5
解二次方程。当你让等式一边等于0，有三种方法可以解一个二次方程。不同人会觉得不同方法会更简单。你可以阅读二次方程式，或者“给二次方程式配方”，或者按照这个因式分解方法例子：
- 例如： $x^{2}+x-6=0$
- 因式分解的目的是找出两个因子相乘得到这个方程。从第一项开始，我们可以将 $x^{2}$ 分为x乘以x。写成(x )(x ) = 0。
- 最后一项为-6。列出每一对相乘为- 6的因子： $-6*1$ 、 $-3*2$ 、 $-2*3$ 和 $-1*6$ 。
- 中间项为x（你可以写成1x）。把每对因子相加，直到得到1为止。正确的因子对为 $-2*3$ ，因为 $-2+3=1$ 。
- 用这对因子来填在空白处： $(x-2)(x+3)=0$ 。
6
留意x的两个解。如果你算得太快，你可能只找到了一个解，却没有意识到还有第二个解。下面是如何找到这两条线相交于两点的两个x值：
- 例如（因式分解）：我们得到方程 $(x-2)(x+3)=0$ 。如果括号中的任意一个因式为0，则这个方程为真。一个解为 $x-2=0$ → $x=2$ 。另一个解为 $x+3=0$ → $x=-3$ 。
- 例如（二次方程或完成平方）：如果你用这些方法来解方程，就会出现平方根。例如，这个方程变成 $x=(-1+{\sqrt {25}})/2$ 。记住，一个平方根可以简化成两个不同的解： ${\sqrt {25}}=5*5$ ，以及 ${\sqrt {25}}=(-5)*(-5)$ 。写出两个方程，每个对应一种可能性，然后分别解出x。
7
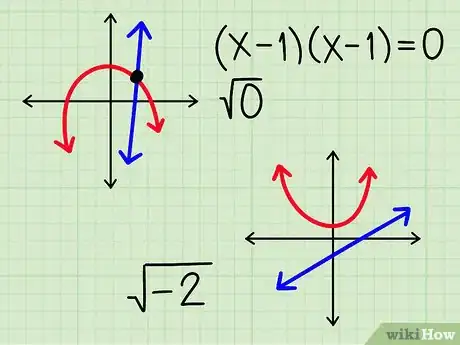
求出一个或零个解。两条几乎没有相交的线只有一个交点，而两条完全不相交的线则没有交点。以下是如何求出这些解：
- 1个解：方程分解成两个相同的因式((x-1)(x-1) = 0)。当代入二次方程时，平方根项是 ${\sqrt {0}}$ 。你只需要解一个方程。
- 无实数解：没有满足要求的因子（对中间项求和）。代入二次方程，得到根号下的负数（例如 ${\sqrt {-2}}$ ）。答案为“无实数解”。
8
把x值代回原方程。求出交点的x值后，把它代回开始时的方程。解出y，求出y值。如果有第二个x值，也重复这个操作。
- 例如：我们求出两个解， $x=2$ ， $x=-3$ 。其中一条直线的方程为 $y=x+7$ 。带入x： $y=2+7$ ， $y=-3+7$ ，然后解出每个方程，得到 $y=9$ ， $y=4$ 。
9
写出交点坐标。现在把答案写成坐标形式，用交点的x值和y值表示。如果你有两个答案，确保匹配正确的x值和y值。
- 例如：当我们带入 $x=2$ ，可以得到 $y=9$ ，所以一个交点为(2, 9)。用同样的方法求出第二个解得出另一个交点为(-3, 4)。
广告

小提示

圆或椭圆的方程有一个 $x^{2}$ 项和一个 $y^{2}$ 项。要想求圆与直线的交点，需要解线性方程中的x。^{[4]
X
研究来源}把x的解代入圆方程，你会得到一个更简单的二次方程。这个方程可能有0个、1个或2个解，如上面的方法所述。
一个圆和一个抛物线（或其他二次型）可能有0、1、2、3或4个解。在两个方程中找出平方的变量——假设它是x²。求出 $x^{2}$ ，并带入另一个方程中的 $x^{2}$ 。求解y，得到0、1、或2个解。把每个解代入原来的二次方程，解出x，每个方程都可能有0、1或2个解。