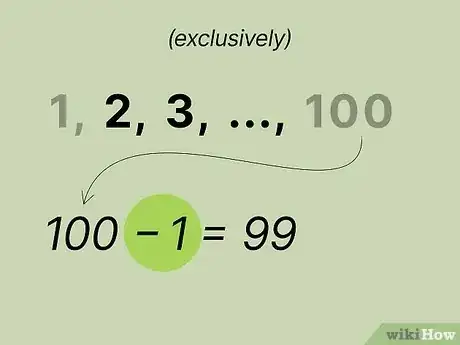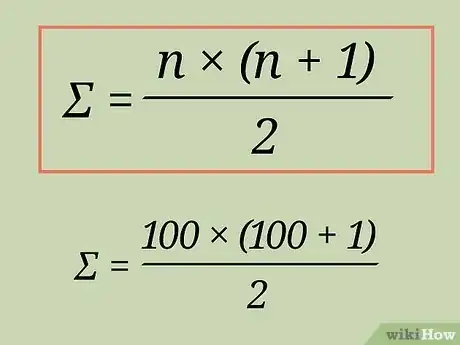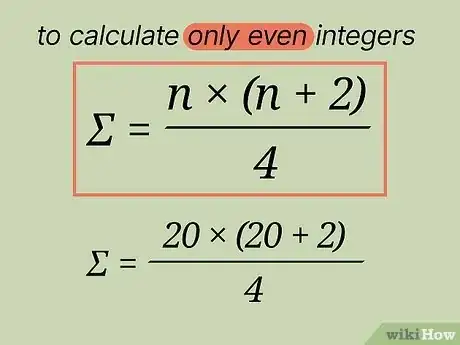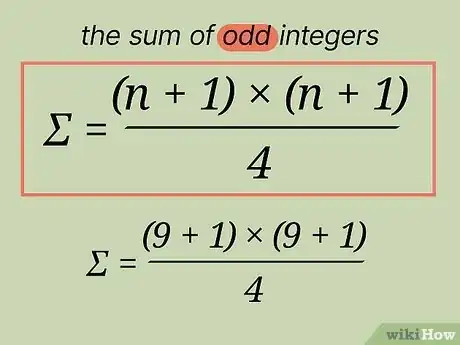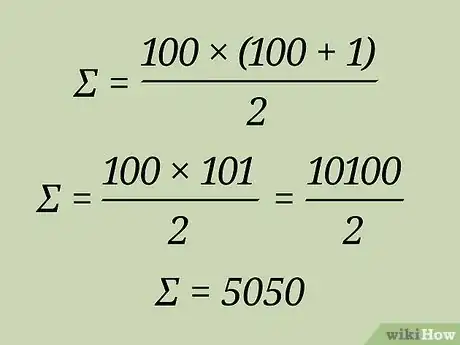如何计算1到N的和

共同创作者是 Grace Imson, MA

如果你正准备参加考试或者只是想快速求出数字的和，可以学习如何将1至 $n$ 相加。因为相加的是整数，所以不用担心分数或小数点。只要选择能算出答案的公式，将问题中的整数代入方程中的 $n$ 并解出方程即可。

方法 1

方法 1 的 2:

1
找出等差数列。仔细看你要相加的数字。如果你想用公式求和，这些数字必须是等差数列。^{[1]
X
研究来源}
- 例如，数列5，6，7，8，9和数列17，19，21，23，25都是等差数列。
- 数列5，6，9，11，14不是等差数列，所以不能用这个公式。
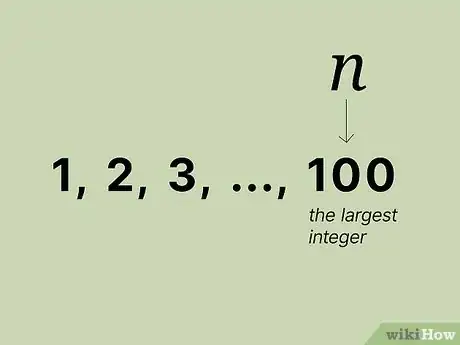
$Step 2 定义序列中的 n {\displaystyle n} 。$

2
定义序列中的 $n$ 。为了用公式算出1到 $n$ $n$ 的和， $n$ $n$ 取最大的那个整数。
- 假设你想求整数1到100之和， $n$ 就是100，因为这是数列中最大的整数。
- 要注意的是，这里相加的是整数，因此 $n$ 不能是小数、分数或负数。
3
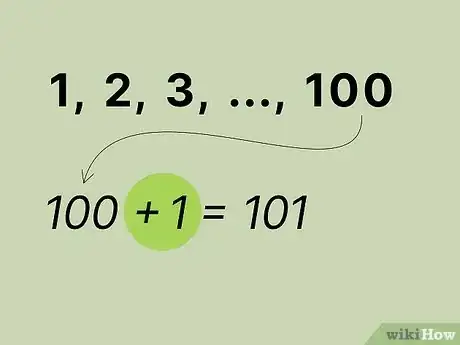
确认有多少个整数相加。为了算出第一个整数到 $n$ $n$ 的和，就得知道相加整数的个数。例如，你要求前200个整数之和，那就有200加1总共201个整数。^{[2]
X
研究来源}
- 如果要算出从1到12的和，就是将12加1共有13个数字。
4
确定是否是求两个数字之间的和。你可能需要求出两个整数之间的整数之和，此时要用 $n$ $n$ 减去1。^{[3]
X
研究来源}
- 假设你只要求出1到100之间的整数之和，要将100减去1得出99。
广告

方法 2

方法 2 的 2:

1
连续整数求和公式。确定要相加的最大整数 $n$ $n$ 后，将该整数代入连续整数的求和公式：整数之和 = $n$ $n$ ∗( $n$ $n$ +1)/2。^{[4]
X
研究来源}
- 例如要求出前100个整数之和，将100代入 $n$ 得出100∗(100+1)/2。
- 如果要求出前20个整数之和， $n$ 用20代入。计算20∗(20+1)/2得出420/2，答案就是210。
2
偶数之和的计算公式。如果题目要求你算出从1开始的偶数之和，那就要用到不同的计算公式了。将最大的整数代入 $n$ $n$ ：偶数之和= $n$ $n$ ∗( $n$ $n$ +2)/4。^{[5]
X
研究来源}
- 假设题目要你求出从1到20的偶数之和， $n$ 为20，公式为 20∗22/4。
3
奇数之和的计算公式。如果题目要你求出奇数之和，需要先找出 $n$ $n$ 。 $n$ $n$ 应该是最大的整数加1。然后代入以下公式：奇数之和= ( $n$ $n$ +1)∗( $n$ $n$ +1)/4。^{[6]
X
研究来源}
- 例如要求出1到9的奇数之和，用9加上1。公式为10∗(10)/4。计算出该公式10∗(10)/4 等于25。
4
自定义公式求和。代入整数之后，根据公式，用整数加上1、2或4再乘以整数；然后将结果除以2或4得出答案。^{[7]
X
研究来源}
- 以连续整数求和的公式为例，100∗101/2，100乘以101等于10100，除以2得出5050。
- 以偶数求和公式为例，20∗22/4，20乘以22得出440，除以4得出110。
广告