詹森多面體列表

詹森多面體是指的所有面都是正多邊形但頂點並非均勻的嚴格凸多面體。即不是柏拉图立体、不是阿基米德立體、不是半正多面體、不是棱柱也不是反棱柱的嚴格凸正多邊形多面體。 1966年，諾曼·詹森發表了一份包含92種有以上性質的多面體列表，並給出了名稱和編號，但他並未證明這種立體僅有92個，但猜想沒有其他的這種立體。[1] 1969年，維克多·扎加勒（Victor Zalgaller）證明了詹森多面體僅有92個，也就是諾曼·詹森給出的多面體列表是完整的。[2]

另外，也可能構造出具有近似於正多邊形面的凸多面體；或可以構造所有面都是正多邊形但不要求嚴格凸的凸多面體。這些多面體被非正式地稱為擬詹森多面體；它們的數量無法被確定，後者則有無窮多種。但後者如果加上一個「條件邊」的條件，則可以確定其數量為78個，稱為條件邊正多邊形凸多面體[3]。詳細的這些立體可以參見條件邊正多邊形凸多面體列表[4]。

下表列出了92種詹森多面體的各項重要性質與數值。每個表都允許按特定欄位的內容來做排序，以便依據特定屬性或性質或詹森多面體的名稱來進行排序。

列表

下表列出詹森多面體的名稱與展開圖：

$J n$	名稱	英語名稱
1	正四角錐	Square pyramid
2	正五角錐	Pentagonal pyramid
3	正三角帳塔	Triangular cupola
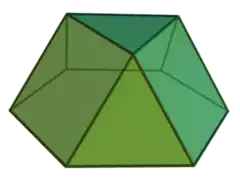4	正四角帳塔	Square cupola
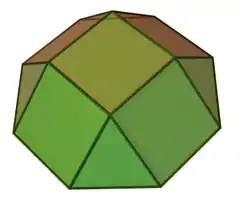5	正五角帳塔	Pentagonal cupola
6	正五角罩帳	Pentagonal rotunda
7	正三角錐柱	Elongated triangular pyramid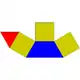
8	正四角錐柱	Elongated square pyramid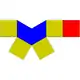
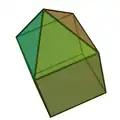9	正五角錐柱	Elongated pentagonal pyramid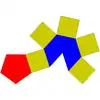
10	四角錐反角柱	Gyroelongated square pyramid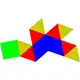
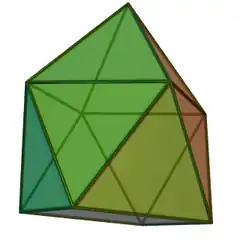11	五角錐反角柱	Gyroelongated pentagonal pyramid
12	雙三角錐	Triangular bipyramid
13	雙五角錐	Pentagonal bipyramid
14	雙三角錐柱	Elongated triangular bipyramid
15	雙四角錐柱	Elongated square bipyramid
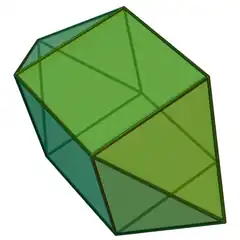16	雙五角錐柱	Elongated pentagonal bipyramid
17	雙四角錐反角柱	Gyroelongated square bipyramid
18	三角帳塔柱	Elongated triangular cupola
19	四角帳塔柱	Elongated square cupola
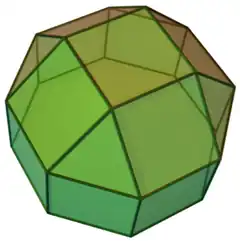20	五角帳塔柱	Elongated pentagonal cupola
21	正五角罩帳柱	Elongated pentagonal rotunda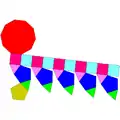
22	正三角帳塔反角柱	Gyroelongated triangular cupola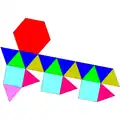
23	正四角帳塔反角柱	Gyroelongated square cupola
24	正五角台塔反角柱	Gyroelongated pentagonal cupola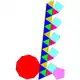
25	正五角罩帳反角柱	Gyroelongated pentagonal rotunda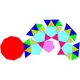
26	異相雙三角柱	Gyrobifastigium
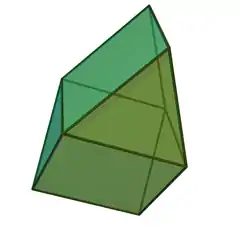27	同相雙三角台塔	Triangular orthobicupola
28	同相雙四角台塔	Square orthobicupola
29	異相雙四角台塔	Square gyrobicupola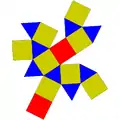
30	同相雙五角台塔	Pentagonal orthobicupola
31	異相雙五角台塔	Pentagonal gyrobicupola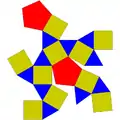
32	同相五角台塔丸塔	Pentagonal orthocupolarotunda
33	異相五角台塔丸塔	Pentagonal gyrocupolarotunda
34	同相雙五角丸塔	Pentagonal orthobirotunda
35	同相雙三角台塔柱	Elongated triangular orthobicupola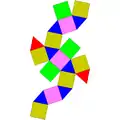
36	異相雙三角台塔柱	Elongated triangular gyrobicupola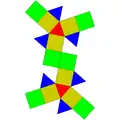
37	異相雙四角台塔柱	Elongated square gyrobicupola
38	同相雙五角台塔柱	Elongated pentagonal orthobicupola
39	異相雙五角台塔柱	Elongated pentagonal gyrobicupola
40	同相五角台塔丸塔柱	Elongated pentagonal orthocupolarotunda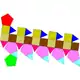
41	異相五角台塔丸塔柱	Elongated pentagonal gyrocupolarotunda
42	同相五角雙丸塔柱	Elongated pentagonal orthobirotunda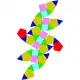
43	異相五角雙丸塔柱	Elongated pentagonal gyrobirotunda
44	雙三角台塔反角柱	Gyroelongated triangular bicupola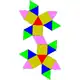
45	雙四角台塔反角柱	Gyroelongated square bicupola
46	雙五角台塔反角柱	Gyroelongated pentagonal bicupola
47	五角台塔丸塔反角柱	Gyroelongated pentagonal cupolarotunda
48	雙五角丸塔反角柱	Gyroelongated pentagonal birotunda
49	側錐三角柱	Augmented triangular prism
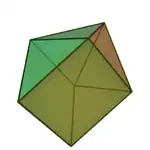50	二側錐三角柱	Biaugmented triangular prism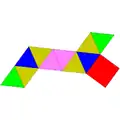
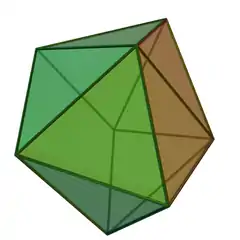51	三側錐三角柱	Triaugmented triangular prism
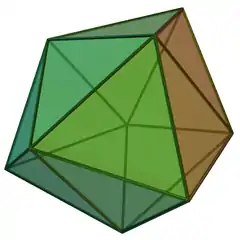52	側錐五角柱	Augmented pentagonal prism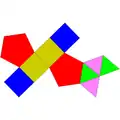
53	間二側錐五角柱	Biaugmented pentagonal prism
54	側錐六角柱	Augmented hexagonal prism
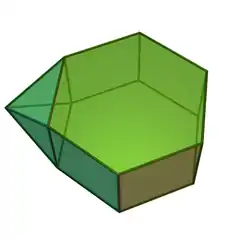55	對二側錐六角柱	Parabiaugmented hexagonal prism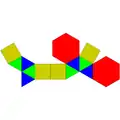
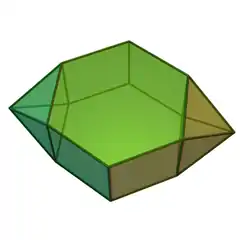56	間二側錐六角柱	Metabiaugmented hexagonal prism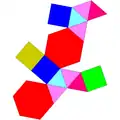
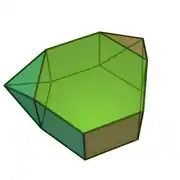57	三側錐六角柱	Triaugmented hexagonal prism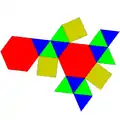
58	侧锥正十二面体	Augmented dodecahedron
59	对二侧锥正十二面体	Parabiaugmented dodecahedron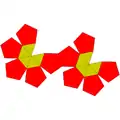
60	间二侧锥正十二面体	Metabiaugmented dodecahedron
61	三侧锥正十二面体	Triaugmented dodecahedron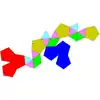
62	正二十面體欠鄰二側錐	Metabidiminished icosahedron
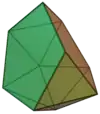63	正二十面體欠三側錐	Tridiminished icosahedron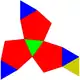
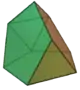64	側錐正二十面體欠三側錐	Augmented tridiminished icosahedron
65	側台塔截角四面體	Augmented truncated tetrahedron
66	側台塔截角立方體	Augmented truncated cube
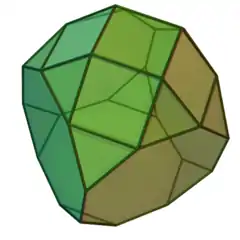67	對二側帳塔截角立方體	Biaugmented truncated cube
68	側台塔截角十二面體	Augmented truncated dodecahedron
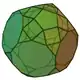69	對二側台塔截角十二面體	Parabiaugmented truncated dodecahedron
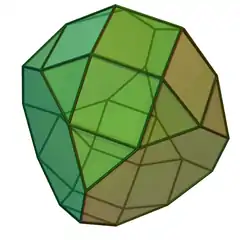
70	間二側台塔截角十二面體	Metabiaugmented truncated dodecahedron
71	三側台塔截角十二面體	Triaugmented truncated dodecahedron
72	單旋側帳塔小斜方截半二十面體	Gyrate rhombicosidodecahedron
73	對二旋側台塔小斜方截半二十面體	Parabigyrate rhombicosidodecahedron
74	鄰二旋側台塔小斜方截半二十面體	Metabigyrate rhombicosidodecahedron
75	三旋側台塔小斜方截半二十面體	Trigyrate rhombicosidodecahedron
76	小斜方截半二十面體欠一側台塔	Diminished rhombicosidodecahedron
77	對單旋側台塔小斜方截半二十面體欠一側台塔	Paragyrate diminished rhombicosidodecahedron
78	鄰單旋側台塔小斜方截半二十面體欠一側台塔	Metagyrate diminished rhombicosidodecahedron
79	二旋側台塔小斜方截半二十面體欠一側台塔	Bigyrate diminished rhombicosidodecahedron
80	小斜方截半二十面體欠對二側帳塔	Parabidiminished rhombicosidodecahedron
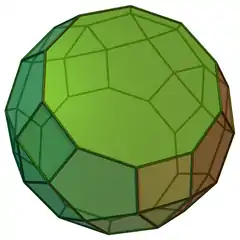81	小斜方截半二十面體欠鄰二側帳塔	Metabidiminished rhombicosidodecahedron
82	單旋側台塔小斜方截半二十面體欠二側台塔	Gyrate bidiminished rhombicosidodecahedron
83	小斜方截半二十面體欠三側台塔	Tridiminished rhombicosidodecahedron
84	扭稜鍥形體	Snub disphenoid
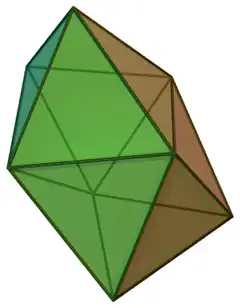85	扭稜四角反角柱	Snub square antiprism
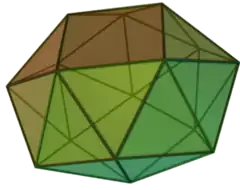86	球狀屋頂	Sphenocorona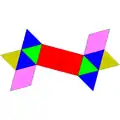
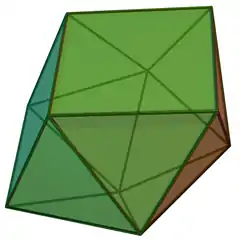87	側錐球狀屋頂	Augmented sphenocorona
88	加長型球狀屋頂	Sphenomegacorona
89	廣底加長型球狀屋頂	Hebesphenomegacorona
90	五角錐球狀屋頂	Disphenocingulum
91	雙新月雙罩帳	Bilunabirotunda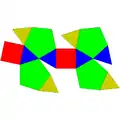
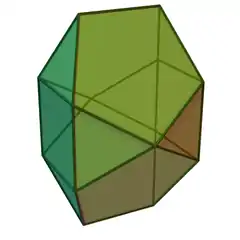92	三角廣底球狀罩帳	Triangular hebesphenorotunda

返回頂部、表格頂部

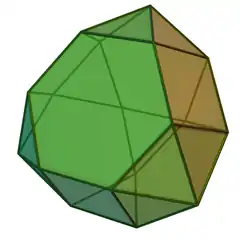說明：

$J n$ – 詹森多面體編號
展開圖 – 立體展開成平面的結果

頂點、邊、面和對稱性

下表列出詹森多面體的頂點數、邊數和面數，以及特定形狀的面數。同時也列出了其對稱性：

$J n$	名稱	V	E	F	F₃	F₄	F₅	F₆	F₈	F₁₀	對稱群	階數
1	正四角錐	5	8	5	4	1					C_4v, [4], (*44)	8
2	正五角錐	6	10	6	5		1				C_5v, [5], (*55)	10
3	正三角帳塔	9	15	8	4	3		1			C_3v, [3], (*33)	6
4	正四角帳塔	12	20	10	4	5			1		C_4v, [4], (*44)	8
5	正五角帳塔	15	25	12	5	5	1			1	C_5v, [5], (*55)	10
6	正五角罩帳	20	35	17	10		6			1	C_5v, [5], (*55)	10
7	正三角錐柱	7	12	7	4	3					C_3v, [3], (*33)	6
8	正四角錐柱	9	16	9	4	5					C_4v, [4], (*44)	8
9	正五角錐柱	11	20	11	5	5	1				C_5v, [5], (*55)	10
10	四角錐反角柱	9	20	13	12	1					C_4v, [4], (*44)	8
11	五角錐反角柱	11	25	16	15		1				C_5v, [5], (*55)	10
12	雙三角錐	5	9	6	6						D_3h, [3,2], (*223)	12
13	雙五角錐	7	15	10	10						D_5h, [5,2], (*225)	20
14	雙三角錐柱	8	15	9	6	3					D_3h, [3,2], (*223)	12
15	雙四角錐柱	10	20	12	8	4					D_4h, [4,2], (*224)	16
16	雙五角錐柱	12	25	15	10	5					D_5h, [5,2], (*225)	20
17	雙四角錐反角柱	10	24	16	16						D_4d, [2⁺,8], (2*4)	16
18	三角帳塔柱	15	27	14	4	9		1			C_3v, [3], (*33)	6
19	四角帳塔柱	20	36	18	4	13			1		C_4v, [4], (*44)	8
20	五角帳塔柱	25	45	22	5	15	1			1	C_5v, [5], (*55)	10
21	正五角罩帳柱	30	55	27	10	10	6			1	C_5v, [5], (*55)	10
22	正三角帳塔反角柱	15	33	20	16	3		1			C_3v, [3], (*33)	6
23	正四角帳塔反角柱	20	44	26	20	5			1		C_4v, [4], (*44)	8
24	正五角台塔反角柱	25	55	32	25	5	1			1	C_5v, [5], (*55)	10
25	正五角罩帳反角柱	30	65	37	30		6			1	C_5v, [5], (*55)	10
26	異相雙三角柱	8	14	8	4	4					D_2d, [2⁺,4], (2*2)	8
27	同相雙三角台塔	12	24	14	8	6					D_3h, [3,2], (*223)	12
28	同相雙四角台塔	16	32	18	8	10					D_4h, [4,2], (*224)	16
29	異相雙四角台塔	16	32	18	8	10					D_4d, [2⁺,8], (2*4)	16
30	同相雙五角台塔	20	40	22	10	10	2				D_5h, [5,2], (*225)	20
31	異相雙五角台塔	20	40	22	10	10	2				D_5d, [2⁺,10], (2*5)	20
32	同相五角台塔丸塔	25	50	27	15	5	7				C_5v, [5], (*55)	10
33	異相五角台塔丸塔	25	50	27	15	5	7				C_5v, [5], (*55)	10
34	同相雙五角丸塔	30	60	32	20		12				D_5h, [5,2], (*225)	20
35	同相雙三角台塔柱	18	36	20	8	12					D_3h, [3,2], (*223)	12
36	異相雙三角台塔柱	18	36	20	8	12					D_3d, [2⁺,6], (2*3)	12
37	異相雙四角台塔柱	24	48	26	8	18					D_4d, [2⁺,8], (2*4)	16
38	同相雙五角台塔柱	30	60	32	10	20	2				D_5h, [5,2], (*225)	20
39	異相雙五角台塔柱	30	60	32	10	20	2				D_5d, [2⁺,10], (2*5)	20
40	同相五角台塔丸塔柱	35	70	37	15	15	7				C_5v, [5], (*55)	10
41	異相五角台塔丸塔柱	35	70	37	15	15	7				C_5v, [5], (*55)	10
42	同相五角雙丸塔柱	40	80	42	20	10	12				D_5h, [5,2], (*225)	20
43	異相五角雙丸塔柱	40	80	42	20	10	12				D_5d, [2⁺,10], (2*5)	20
44	雙三角台塔反角柱	18	42	26	20	6					D₃, [3,2]⁺,(223)	6
45	雙四角台塔反角柱	24	56	34	24	10					D₄, [4,2]⁺, (224)	8
46	雙五角台塔反角柱	30	70	42	30	10	2				D₅, [5,2]⁺, (225)	10
47	五角台塔丸塔反角柱	35	80	47	35	5	7				C₅, [5]⁺, (55)	5
48	雙五角丸塔反角柱	40	90	52	40		12				D₅, [5,2]⁺, (225)	10
49	側錐三角柱	7	13	8	6	2					C_2v, [2], (*22)	4
50	二側錐三角柱	8	17	11	10	1					C_2v, [2], (*22)	4
51	三側錐三角柱	9	21	14	14						D_3h, [3,2], (*223)	12
52	側錐五角柱	11	19	10	4	4	2				C_2v, [2], (*22)	4
53	間二側錐五角柱	12	23	13	8	3	2				C_2v, [2], (*22)	4
54	側錐六角柱	13	22	11	4	5		2			C_2v, [2], (*22)	4
55	對二側錐六角柱	14	26	14	8	4		2			D_2h, [2,2], (*222)	8
56	間二側錐六角柱	14	26	14	8	4		2			C_2v, [2], (*22)	4
57	三側錐六角柱	15	30	17	12	3		2			D_3h, [3,2], (*223)	12
58	侧锥正十二面体	21	35	16	5		11				C_5v, [5], (*55)	10
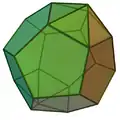
59	对二侧锥正十二面体	22	40	20	10		10				D_5d, [2⁺,10], (2*5)	20
60	间二侧锥正十二面体	22	40	20	10		10				C_2v, [2], (*22)	4
61	三侧锥正十二面体	23	45	24	15		9				C_3v, [3], (*33)	6
62	正二十面體欠鄰二側錐	10	20	12	10		2				C_2v, [2], (*22)	4
63	正二十面體欠三側錐	9	15	8	5		3				C_3v, [3], (*33)	6
64	側錐正二十面體欠三側錐	10	18	10	7		3				C_3v, [3], (*33)	6
65	側台塔截角四面體	15	27	14	8	3		3			C_3v, [3], (*33)	6
66	側台塔截角立方體	28	48	22	12	5			5		C_4v, [4], (*44)	8
67	對二側帳塔截角立方體	32	60	30	16	10			4		D_4h, [4,2], (*224)	16
68	側台塔截角十二面體	65	105	42	25	5	1			11	C_5v, [5], (*55)	10
69	對二側台塔截角十二面體	70	120	52	30	10	2			10	D_5d, [2⁺,10], (2*5)	20
70	間二側台塔截角十二面體	70	120	52	30	10	2			10	C_2v, [2], (*22)	4
71	三側台塔截角十二面體	75	135	62	35	15	3			9	C_3v, [3], (*33)	6
72	單旋側帳塔小斜方截半二十面體	60	120	62	20	30	12				C_5v, [5], (*55)	10
73	對二旋側台塔小斜方截半二十面體	60	120	62	20	30	12				D_5d, [2⁺,10], (2*5)	20
74	鄰二旋側台塔小斜方截半二十面體	60	120	62	20	30	12				C_2v, [2], (*22)	4
75	三旋側台塔小斜方截半二十面體	60	120	62	20	30	12				C_3v, [3], (*33)	6
76	小斜方截半二十面體欠一側台塔	55	105	52	15	25	11			1	C_5v, [5], (*55)	10
77	對單旋側台塔小斜方截半二十面體欠一側台塔	55	105	52	15	25	11			1	C_5v, [5], (*55)	10
78	鄰單旋側台塔小斜方截半二十面體欠一側台塔	55	105	52	15	25	11			1	C_s, [ ], (*11)	2
79	二旋側台塔小斜方截半二十面體欠一側台塔	55	105	52	15	25	11			1	C_s, [ ], (*11)	2
80	小斜方截半二十面體欠對二側帳塔	50	90	42	10	20	10			2	D_5d, [2⁺,10], (2*5)	20
81	小斜方截半二十面體欠鄰二側帳塔	50	90	42	10	20	10			2	C_2v, [2], (*22)	4
82	單旋側台塔小斜方截半二十面體欠二側台塔	50	90	42	10	20	10			2	C_s, [ ], (*11)	2
83	小斜方截半二十面體欠三側台塔	45	75	32	5	15	9			3	C_3v, [3], (*33)	6
84	扭稜鍥形體	8	18	12	12						D_2d, [2⁺,4], (2*2)	8
85	扭稜四角反角柱	16	40	26	24	2					D_4d, [2⁺,8], (2*4)	16
86	球狀屋頂	10	22	14	12	2					C_2v, [2], (*22)	4
87	側錐球狀屋頂	11	26	17	16	1					C_s, [ ], (*11)	2
88	加長型球狀屋頂	12	28	18	16	2					C_2v, [2], (*22)	4
89	廣底加長型球狀屋頂	14	33	21	18	3					C_2v, [2], (*22)	4
90	五角錐球狀屋頂	16	38	24	20	4					D_2d, [2⁺,4], (2*2)	8
91	雙新月雙罩帳	14	26	14	8	2	4				D_2h, [2,2], (*222)	8
92	三角廣底球狀罩帳	18	36	20	13	3	3	1			C_3v, [3], (*33)	6

返回頂部、表格頂部

說明：

$J n$ – 詹森多面體編號
V – 頂點的數量
E – 邊的數量
F – 面（所有的面）的數量
F_n – 僅n邊形面的數量
F₃～F₁₀ – F₃：面為三角形的面的數量、F₄：面為正方形的面的數量……以此類推

其中，正四角錐（ $J 1$ ）有最少的頂點（5個）、最少的邊（8條）和最少的面（5個）。

三側台塔截角十二面體 $J 71$ 具有最多的頂點（75個）和最多的邊（135條）。它的面數也是最多的（62個），其他還有單旋側帳塔小斜方截半二十面體 $J 72$ 、對二旋側台塔小斜方截半二十面體 $J 73$ 、鄰二旋側台塔小斜方截半二十面體 $J 74$ 和三旋側台塔小斜方截半二十面體 $J 75$ 。

表面積

由於詹森多面體的所有面都是由正三角形、正方形、正五邊形、正六邊形、正八邊形或正十邊形所組成，代表著其面的邊數僅會有3、4、5、6、8或10條，且為正多邊形，因此這些正多邊形面都會具有相同的邊長 $a$ ，因此詹森多面體的表面積 $A$ 可由下式計算得到：

A=\sum _{n=3,4,5,6,8,10}F_{n}A_{n}

其中 $F n$ 是上表中的多邊形面數，且正 $n$ 邊形的面積 $A n$ 也可由下式計算得到：

A_{n}=\left({\frac {n}{4}}\cot {\frac {\pi }{n}}\right)a^{2}

在詹森多面體的例子中，組成其的正多邊形僅有正三角形、正方形、正五邊形、正六邊形、正八邊形或正十邊形，而我們有正三角形的面積 $A 3$ 、正方形的面積 $A 4$ 、正五邊形的面積 $A 5$ 、正六邊形的面積 $A 6$ 、正八邊形 $A 8$ 的面積和正十邊形 $A 10$ 的面積公式：

A_{3}={\frac {1}{4}}{\sqrt {3}}\,a^{2}

A_{4}=a^{2}

A_{5}={\frac {1}{4}}{\sqrt {5(5+2{\sqrt {5}})}}\,a^{2}

A_{6}={\frac {3}{2}}{\sqrt {3}}\,a^{2}

A_{8}=2(1+{\sqrt {2}})\,a^{2}

A_{10}={\frac {5}{2}}{\sqrt {5+2{\sqrt {5}}}}\,a^{2},

因此可以得出下表的詹森多面體表面積。

$J n$	多面體名稱	$A / a 2$ （近似值）	$A / a 2$ （精確值）
1	正四角錐	2.732050808	$1+{\sqrt {3}}$
2	正五角錐	3.885540910	${\frac {1}{4}}\left(5{\sqrt {3}}+{\sqrt {5\left(5+2{\sqrt {5}}\right)}}\right)$
3	正三角帳塔	7.330127019	${\frac {1}{2}}\left(6+5{\sqrt {3}}\right)$
4	正四角帳塔	11.560477932	$7+2{\sqrt {2}}+{\sqrt {3}}$
5	正五角帳塔	16.579749753	${\frac {1}{4}}\left(20+5{\sqrt {3}}+10{\sqrt {5+2{\sqrt {5}}}}+{\sqrt {5\left(5+2{\sqrt {5}}\right)}}\right)$
6	正五角罩帳	22.347200265	${\frac {1}{2}}\left(5{\sqrt {3}}+5{\sqrt {5+2{\sqrt {5}}}}+3{\sqrt {5\left(5+2{\sqrt {5}}\right)}}\right)$
7	正三角錐柱	4.732050808	$3+{\sqrt {3}}$
8	正四角錐柱	6.732050808	$5+{\sqrt {3}}$
9	正五角錐柱	8.885540910	${\frac {1}{4}}\left(20+5{\sqrt {3}}+{\sqrt {5\left(5+2{\sqrt {5}}\right)}}\right)$
10	正四角錐反角柱	6.196152423	$1+3{\sqrt {3}}$
11	正五角錐反角柱	8.215667929	${\frac {1}{4}}\left(15{\sqrt {3}}+{\sqrt {5\left(5+2{\sqrt {5}}\right)}}\right)$
12	雙三角錐	2.598076211	${\frac {3{\sqrt {3}}}{2}}$
13	雙五角錐	4.330127019	${\frac {5{\sqrt {3}}}{2}}$
14	雙三角錐柱	5.598076211	${\frac {3}{2}}\left(2+{\sqrt {3}}\right)$
15	雙四角錐柱	7.464101615	$2\left(2+{\sqrt {3}}\right)$
16	雙五角錐柱	9.330127019	${\frac {5}{2}}\left(2+{\sqrt {3}}\right)$
17	雙四角錐反角柱	6.928203230	$4{\sqrt {3}}$
18	三角帳塔柱	13.330127019	${\frac {1}{2}}\left(18+5{\sqrt {3}}\right)$
19	四角帳塔柱	19.560477932	$15+2{\sqrt {2}}+{\sqrt {3}}$
20	五角帳塔柱	26.579749753	${\frac {1}{4}}\left(60+5{\sqrt {3}}+10{\sqrt {5+2{\sqrt {5}}}}+{\sqrt {5\left(5+2{\sqrt {5}}\right)}}\right)$
21	正五角罩帳柱	32.347200265	${\frac {1}{2}}\left(20+5{\sqrt {3}}+5{\sqrt {5+2{\sqrt {5}}}}+3{\sqrt {5\left(5+2{\sqrt {5}}\right)}}\right)$
22	正三角帳塔反角柱	12.526279442	${\frac {1}{2}}\left(6+11{\sqrt {3}}\right)$
23	正四角帳塔反角柱	18.488681163	$7+2{\sqrt {2}}+5{\sqrt {3}}$
24	正五角台塔反角柱	25.240003791	${\frac {1}{4}}\left(20+25{\sqrt {3}}+10{\sqrt {5+2{\sqrt {5}}}}+{\sqrt {5\left(5+2{\sqrt {5}}\right)}}\right)$
25	正五角罩帳反角柱	31.007454303	${\frac {1}{2}}\left(15{\sqrt {3}}+5{\sqrt {5+2{\sqrt {5}}}}+3{\sqrt {5\left(5+2{\sqrt {5}}\right)}}\right)$
26	異相雙三角柱	5.732050808	$4+{\sqrt {3}}$
27	同相雙三角台塔	9.464101615	$2\left(3+{\sqrt {3}}\right)$
28	同相雙四角台塔	13.464101615	$2\left(5+{\sqrt {3}}\right)$
29	異相雙四角台塔	13.464101615	$2\left(5+{\sqrt {3}}\right)$
30	同相雙五角台塔	17.771081820	${\frac {1}{2}}\left(20+5{\sqrt {3}}+{\sqrt {5\left(5+2{\sqrt {5}}\right)}}\right)$
31	異相雙五角台塔	17.771081820	${\frac {1}{2}}\left(20+5{\sqrt {3}}+{\sqrt {5\left(5+2{\sqrt {5}}\right)}}\right)$
32	同相五角台塔丸塔	23.538532333	${\frac {1}{4}}\left(20+15{\sqrt {3}}+7{\sqrt {5\left(5+2{\sqrt {5}}\right)}}\right)$
33	異相五角台塔丸塔	23.538532333	${\frac {1}{4}}\left(20+15{\sqrt {3}}+7{\sqrt {5\left(5+2{\sqrt {5}}\right)}}\right)$
34	同相雙五角丸塔	29.305982845	$5{\sqrt {3}}+3{\sqrt {5\left(5+2{\sqrt {5}}\right)}}$
35	同相雙三角台塔柱	15.464101615	$2\left(6+{\sqrt {3}}\right)$
36	異相雙三角台塔柱	15.464101615	$2\left(6+{\sqrt {3}}\right)$
37	異相雙四角台塔柱	21.464101615	$2\left(9+{\sqrt {3}}\right)$
38	同相雙五角台塔柱	27.771081820	${\frac {1}{2}}\left(40+5{\sqrt {3}}+{\sqrt {5\left(5+2{\sqrt {5}}\right)}}\right)$
39	異相雙五角台塔柱	27.771081820	${\frac {1}{2}}\left(40+5{\sqrt {3}}+{\sqrt {5\left(5+2{\sqrt {5}}\right)}}\right)$
40	同相五角台塔丸塔柱	33.538532333	${\frac {1}{4}}\left(60+15{\sqrt {3}}+7{\sqrt {5\left(5+2{\sqrt {5}}\right)}}\right)$
41	異相五角台塔丸塔柱	33.538532333	${\frac {1}{4}}\left(60+15{\sqrt {3}}+7{\sqrt {5\left(5+2{\sqrt {5}}\right)}}\right)$
42	同相五角雙丸塔柱	39.305982845	$10+5{\sqrt {3}}+3{\sqrt {5\left(5+2{\sqrt {5}}\right)}}$
43	異相五角雙丸塔柱	39.305982845	$10+5{\sqrt {3}}+3{\sqrt {5\left(5+2{\sqrt {5}}\right)}}$
44	雙三角台塔反角柱	14.660254038	$6+5{\sqrt {3}}$
45	雙四角台塔反角柱	20.392304845	$2\left(5+3{\sqrt {3}}\right)$
46	雙五角台塔反角柱	26.431335858	${\frac {1}{2}}\left(20+15{\sqrt {3}}+{\sqrt {5\left(5+2{\sqrt {5}}\right)}}\right)$
47	五角台塔丸塔反角柱	32.198786370	${\frac {1}{4}}\left(20+35{\sqrt {3}}+7{\sqrt {5\left(5+2{\sqrt {5}}\right)}}\right)$
48	雙五角丸塔反角柱	37.966236883	$10{\sqrt {3}}+3{\sqrt {5\left(5+2{\sqrt {5}}\right)}}$
49	側錐三角柱	4.598076211	${\frac {1}{2}}\left(4+3{\sqrt {3}}\right)$
50	二側錐三角柱	5.330127019	${\frac {1}{2}}\left(2+5{\sqrt {3}}\right)$
51	三側錐三角柱	6.062177826	${\frac {7{\sqrt {3}}}{2}}$
52	側錐五角柱	9.173005609	${\frac {1}{2}}\left(8+2{\sqrt {3}}+{\sqrt {5\left(5+2{\sqrt {5}}\right)}}\right)$
53	間二側錐五角柱	9.905056416	${\frac {1}{2}}\left(6+4{\sqrt {3}}+{\sqrt {5\left(5+2{\sqrt {5}}\right)}}\right)$
54	側錐六角柱	11.928203230	$5+4{\sqrt {3}}$
55	對二側錐六角柱	12.660254038	$4+5{\sqrt {3}}$
56	間二側錐六角柱	12.660254038	$4+5{\sqrt {3}}$
57	三側錐六角柱	13.392304845	$3\left(1+2{\sqrt {3}}\right)$
58	侧锥正十二面体	21.090314916	${\frac {1}{4}}\left(5{\sqrt {3}}+11{\sqrt {5\left(5+2{\sqrt {5}}\right)}}\right)$
59	对二侧锥正十二面体	21.534901025	${\frac {5}{2}}\left({\sqrt {3}}+{\sqrt {5\left(5+2{\sqrt {5}}\right)}}\right)$
60	间二侧锥正十二面体	21.534901025	${\frac {5}{2}}\left({\sqrt {3}}+{\sqrt {5\left(5+2{\sqrt {5}}\right)}}\right)$
61	三侧锥正十二面体	21.979487134	${\frac {3}{4}}\left(5{\sqrt {3}}+3{\sqrt {5\left(5+2{\sqrt {5}}\right)}}\right)$
62	正二十面體欠鄰二側錐	7.771081820	${\frac {1}{2}}\left(5{\sqrt {3}}+{\sqrt {5\left(5+2{\sqrt {5}}\right)}}\right)$
63	正二十面體欠三側錐	7.326495711	${\frac {1}{4}}\left(5{\sqrt {3}}+3{\sqrt {5\left(5+2{\sqrt {5}}\right)}}\right)$
64	側錐正二十面體欠三側錐	8.192521115	${\frac {1}{4}}\left(7{\sqrt {3}}+3{\sqrt {5\left(5+2{\sqrt {5}}\right)}}\right)$
65	側台塔截角四面體	14.258330249	${\frac {1}{2}}\left(6+13{\sqrt {3}}\right)$
66	側台塔截角立方體	34.338288046	$15+10{\sqrt {2}}+3{\sqrt {3}}$
67	對二側帳塔截角立方體	36.241911729	$2\left(9+4{\sqrt {2}}+2{\sqrt {3}}\right)$
68	側台塔截角十二面體	102.182092220	${\frac {1}{4}}\left(20+25{\sqrt {3}}+110{\sqrt {5+2{\sqrt {5}}}}+{\sqrt {5\left(5+2{\sqrt {5}}\right)}}\right)$
69	對二側台塔截角十二面體	103.373424287	${\frac {1}{2}}\left(20+15{\sqrt {3}}+50{\sqrt {5+2{\sqrt {5}}}}+{\sqrt {5\left(5+2{\sqrt {5}}\right)}}\right)$
70	間二側台塔截角十二面體	103.373424287	${\frac {1}{2}}\left(20+15{\sqrt {3}}+50{\sqrt {5+2{\sqrt {5}}}}+{\sqrt {5\left(5+2{\sqrt {5}}\right)}}\right)$
71	三側台塔截角十二面體	104.564756354	${\frac {1}{4}}\left(60+35{\sqrt {3}}+90{\sqrt {5+2{\sqrt {5}}}}+3{\sqrt {5\left(5+2{\sqrt {5}}\right)}}\right)$
72	單旋側帳塔小斜方截半二十面體	59.305982845	$30+5{\sqrt {3}}+3{\sqrt {5\left(5+2{\sqrt {5}}\right)}}$
73	對二旋側台塔小斜方截半二十面體	59.305982845	$30+5{\sqrt {3}}+3{\sqrt {5\left(5+2{\sqrt {5}}\right)}}$
74	鄰二旋側台塔小斜方截半二十面體	59.305982845	$30+5{\sqrt {3}}+3{\sqrt {5\left(5+2{\sqrt {5}}\right)}}$
75	三旋側台塔小斜方截半二十面體	59.305982845	$30+5{\sqrt {3}}+3{\sqrt {5\left(5+2{\sqrt {5}}\right)}}$
76	小斜方截半二十面體欠一側台塔	58.114650778	${\frac {1}{4}}\left(100+15{\sqrt {3}}+10{\sqrt {5+2{\sqrt {5}}}}+11{\sqrt {5\left(5+2{\sqrt {5}}\right)}}\right)$
77	對單旋側台塔小斜方截半二十面體欠一側台塔	58.114650778	${\frac {1}{4}}\left(100+15{\sqrt {3}}+10{\sqrt {5+2{\sqrt {5}}}}+11{\sqrt {5\left(5+2{\sqrt {5}}\right)}}\right)$
78	鄰單旋側台塔小斜方截半二十面體欠一側台塔	58.114650778	${\frac {1}{4}}\left(100+15{\sqrt {3}}+10{\sqrt {5+2{\sqrt {5}}}}+11{\sqrt {5\left(5+2{\sqrt {5}}\right)}}\right)$
79	二旋側台塔小斜方截半二十面體欠一側台塔	58.114650778	${\frac {1}{4}}\left(100+15{\sqrt {3}}+10{\sqrt {5+2{\sqrt {5}}}}+11{\sqrt {5\left(5+2{\sqrt {5}}\right)}}\right)$
80	小斜方截半二十面體欠對二側帳塔	56.923318711	${\frac {5}{2}}\left(8+{\sqrt {3}}+2{\sqrt {5+2{\sqrt {5}}}}+{\sqrt {5\left(5+2{\sqrt {5}}\right)}}\right)$
81	小斜方截半二十面體欠鄰二側帳塔	56.923318711	${\frac {5}{2}}\left(8+{\sqrt {3}}+2{\sqrt {5+2{\sqrt {5}}}}+{\sqrt {5\left(5+2{\sqrt {5}}\right)}}\right)$
82	單旋側台塔小斜方截半二十面體欠二側台塔	56.923318711	${\frac {5}{2}}\left(8+{\sqrt {3}}+2{\sqrt {5+2{\sqrt {5}}}}+{\sqrt {5\left(5+2{\sqrt {5}}\right)}}\right)$
83	小斜方截半二十面體欠三側台塔	55.731986644	${\frac {1}{4}}\left(60+5{\sqrt {3}}+30{\sqrt {5+2{\sqrt {5}}}}+9{\sqrt {5\left(5+2{\sqrt {5}}\right)}}\right)$
84	扭稜鍥形體	5.196152423	$3{\sqrt {3}}$
85	扭稜四角反角柱	12.392304845	$2\left(1+3{\sqrt {3}}\right)$
86	球狀屋頂	7.196152423	$2+3{\sqrt {3}}$
87	側錐球狀屋頂	7.928203230	$1+4{\sqrt {3}}$
88	加長型球狀屋頂	8.928203230	$2\left(1+2{\sqrt {3}}\right)$
89	廣底加長型球狀屋頂	10.794228634	${\frac {3}{2}}\left(2+3{\sqrt {3}}\right)$
90	五角錐球狀屋頂	12.660254038	$4+5{\sqrt {3}}$
91	雙新月雙罩帳	12.346011217	$2+2{\sqrt {3}}+{\sqrt {5\left(5+2{\sqrt {5}}\right)}}$
92	三角廣底球狀罩帳	16.388673538	${\frac {1}{4}}\left(12+19{\sqrt {3}}+3{\sqrt {5\left(5+2{\sqrt {5}}\right)}}\right)$

在固定邊長的條件下，雙三角錐 $J 12$ 的表面積最小，而三側台塔截角十二面體 $J 71$ 的表面積最大，兩者相差40倍以上。

體積

下表列出了詹森多面體的體積。在這個表格中， $V$ 代表體積（不是第一個表中的頂點數），而 $a$ 代表邊長。

表格的資料來源是沃尔夫勒姆研究公司的Mathematica軟體中提供的PolyhedronData[..., "Volume"]計算多面體體積的指令。

詹森多面體的體積也可以根據其頂點座標來計算出來。如果邊長是固定的，那麼所有92個詹森多面體的頂點座標就都是已知的。如此一來，就可以用此資訊來計算體積。概念上最簡單的作法是：對要算體積的詹森多面體之表面做三角化，例如在每個非三角形面的中心添加一個額外的點，然後將之與該面的其他頂點連接構成多個三角形（並不是所有凸多面體都可以不添加額外頂點就完成三角剖分[5]）。完成表面的三角化後選擇一些內部點作為“原點”，這樣就可以把表面的三角形與內部所選的點構造成不規則四面體。這些不規則四面體在多面體內部有一個頂點、在多面體表面有3個頂點，而詹森多面體的體積就是這些不規則四面體的體積總和。不規則四面體的體積可以透過公式計算。

$J n$	多面體名稱	$V / a 3$ （近似值）	$V / a 3$ （精確值）
1	正四角錐	0.235702260	${\frac {1}{3{\sqrt {2}}}}$
2	正五角錐	0.301502832	${\frac {1}{24}}\left(5+{\sqrt {5}}\right)$
3	正三角帳塔	1.178511302	${\frac {5}{3{\sqrt {2}}}}$
4	正四角帳塔	1.942809042	$1+{\frac {2{\sqrt {2}}}{3}}$
5	正五角帳塔	2.324045318	${\frac {1}{6}}\left(5+4{\sqrt {5}}\right)$
6	正五角罩帳	6.917762968	${\frac {1}{12}}\left(45+17{\sqrt {5}}\right)$
7	正三角錐柱	0.550863832	${\frac {1}{12}}\left({\sqrt {2}}+3{\sqrt {3}}\right)$
8	正四角錐柱	1.235702260	${\frac {1}{6}}\left(6+{\sqrt {2}}\right)$
9	正五角錐柱	2.021980233	${\frac {1}{24}}\left(5+{\sqrt {5}}+6{\sqrt {5\left(5+2{\sqrt {5}}\right)}}\right)$
10	正四角錐反角柱	1.192702242	${\frac {1}{6}}\left({\sqrt {2}}+2{\sqrt {4+3{\sqrt {2}}}}\right)$
11	正五角錐反角柱	1.880192158	${\frac {1}{24}}\left(25+9{\sqrt {5}}\right)$
12	雙三角錐	0.235702260	${\frac {1}{3{\sqrt {2}}}}$
13	雙五角錐	0.603005665	${\frac {1}{12}}\left(5+{\sqrt {5}}\right)$
14	雙三角錐柱	0.668714962	${\frac {1}{12}}\left(2{\sqrt {2}}+3{\sqrt {3}}\right)$
15	雙四角錐柱	1.471404521	${\frac {1}{3}}\left(3+{\sqrt {2}}\right)$
16	雙五角錐柱	2.323483065	${\frac {1}{12}}\left(5+{\sqrt {5}}+3{\sqrt {5\left(5+2{\sqrt {5}}\right)}}\right)$
17	雙四角錐反角柱	1.428404503	${\frac {1}{3}}\left({\sqrt {2}}+{\sqrt {4+3{\sqrt {2}}}}\right)$
18	三角帳塔柱	3.776587513	${\frac {1}{6}}\left(5{\sqrt {2}}+9{\sqrt {3}}\right)$
19	四角帳塔柱	6.771236166	$3+{\frac {8{\sqrt {2}}}{3}}$
20	五角帳塔柱	10.018254161	${\frac {1}{6}}\left(5+4{\sqrt {5}}+15{\sqrt {5+2{\sqrt {5}}}}\right)$
21	正五角罩帳柱	14.611971811	${\frac {1}{12}}\left(45+17{\sqrt {5}}+30{\sqrt {5+2{\sqrt {5}}}}\right)$
22	正三角帳塔反角柱	3.516053091	${\frac {1}{3}}{\sqrt {{\frac {61}{2}}+18{\sqrt {3}}+30{\sqrt {1+{\sqrt {3}}}}}}$
23	正四角帳塔反角柱	6.210765792	8次方程的根
24	正五角台塔反角柱	9.073333194	8次方程的根
25	正五角罩帳反角柱	13.667050844	8次方程的根
26	異相雙三角柱	0.866025404	${\frac {\sqrt {3}}{2}}$
27	同相雙三角台塔	2.357022604	${\frac {5{\sqrt {2}}}{3}}$
28	同相雙四角台塔	3.885618083	$2+{\frac {4{\sqrt {2}}}{3}}$
29	異相雙四角台塔	3.885618083	$2+{\frac {4{\sqrt {2}}}{3}}$
30	同相雙五角台塔	4.648090637	${\frac {1}{3}}\left(5+4{\sqrt {5}}\right)$
31	異相雙五角台塔	4.648090637	${\frac {1}{3}}\left(5+4{\sqrt {5}}\right)$
32	同相五角台塔丸塔	9.241808286	${\frac {5}{12}}\left(11+5{\sqrt {5}}\right)$
33	異相五角台塔丸塔	9.241808286	${\frac {5}{12}}\left(11+5{\sqrt {5}}\right)$
34	同相雙五角丸塔	13.835525936	${\frac {1}{6}}\left(45+17{\sqrt {5}}\right)$
35	同相雙三角台塔柱	4.955098815	${\frac {5{\sqrt {2}}}{3}}+{\frac {3{\sqrt {3}}}{2}}$
36	異相雙三角台塔柱	4.955098815	${\frac {5{\sqrt {2}}}{3}}+{\frac {3{\sqrt {3}}}{2}}$
37	異相雙四角台塔柱	8.714045208	$4+{\frac {10{\sqrt {2}}}{3}}$
38	同相雙五角台塔柱	12.342299480	${\frac {1}{6}}\left(10+8{\sqrt {5}}+15{\sqrt {5+2{\sqrt {5}}}}\right)$
39	異相雙五角台塔柱	12.342299480	${\frac {1}{6}}\left(10+8{\sqrt {5}}+15{\sqrt {5+2{\sqrt {5}}}}\right)$
40	同相五角台塔丸塔柱	16.936017129	${\frac {5}{12}}\left(11+5{\sqrt {5}}+6{\sqrt {5+2{\sqrt {5}}}}\right)$
41	異相五角台塔丸塔柱	16.936017129	${\frac {5}{12}}\left(11+5{\sqrt {5}}+6{\sqrt {5+2{\sqrt {5}}}}\right)$
42	同相五角雙丸塔柱	21.529734779	${\frac {1}{6}}\left(45+17{\sqrt {5}}+15{\sqrt {5+2{\sqrt {5}}}}\right)$
43	異相五角雙丸塔柱	21.529734779	${\frac {1}{6}}\left(45+17{\sqrt {5}}+15{\sqrt {5+2{\sqrt {5}}}}\right)$
44	雙三角台塔反角柱	4.694564393	${\frac {1}{3}}{\sqrt {68+18{\sqrt {3}}+60{\sqrt {1+{\sqrt {3}}}}}}$
45	雙四角台塔反角柱	8.153574834	8次方程的根
46	雙五角台塔反角柱	11.397378512	8次方程的根
47	五角台塔丸塔反角柱	15.991096162	8次方程的根
48	雙五角丸塔反角柱	20.584813812	8次方程的根
49	側錐三角柱	0.668714962	${\frac {1}{12}}\left(2{\sqrt {2}}+3{\sqrt {3}}\right)$
50	二側錐三角柱	0.904417223	${\sqrt {{\frac {59}{144}}+{\frac {1}{\sqrt {6}}}}}$
51	三側錐三角柱	1.140119483	${\frac {1}{\sqrt {2}}}+{\frac {\sqrt {3}}{4}}$
52	側錐五角柱	1.956179661	${\frac {1}{12}}{\sqrt {233+90{\sqrt {5}}+12{\sqrt {50+20{\sqrt {5}}}}}}$
53	間二側錐五角柱	2.191881921	${\frac {1}{12}}{\sqrt {257+90{\sqrt {5}}+24{\sqrt {50+20{\sqrt {5}}}}}}$
54	側錐六角柱	2.833778472	${\frac {1}{6}}\left({\sqrt {2}}+9{\sqrt {3}}\right)$
55	對二側錐六角柱	3.069480732	${\frac {1}{6}}\left(2{\sqrt {2}}+9{\sqrt {3}}\right)$
56	間二側錐六角柱	3.069480732	${\frac {1}{6}}\left(2{\sqrt {2}}+9{\sqrt {3}}\right)$
57	三側錐六角柱	3.305182993	${\frac {1}{\sqrt {2}}}+{\frac {3{\sqrt {3}}}{2}}$
58	侧锥正十二面体	7.964621793	${\frac {1}{24}}\left(95+43{\sqrt {5}}\right)$
59	对二侧锥正十二面体	8.266124625	${\frac {1}{6}}\left(25+11{\sqrt {5}}\right)$
60	间二侧锥正十二面体	8.266124625	${\frac {1}{6}}\left(25+11{\sqrt {5}}\right)$
61	三侧锥正十二面体	8.567627458	${\frac {5}{8}}\left(7+3{\sqrt {5}}\right)$
62	正二十面體欠鄰二側錐	1.578689326	${\frac {1}{6}}\left(5+2{\sqrt {5}}\right)$
63	正二十面體欠三側錐	1.277186493	${\frac {5}{8}}+{\frac {7{\sqrt {5}}}{24}}$
64	側錐正二十面體欠三側錐	1.395037624	${\frac {1}{24}}\left(15+2{\sqrt {2}}+7{\sqrt {5}}\right)$
65	側台塔截角四面體	3.889087297	${\frac {11}{2{\sqrt {2}}}}$
66	側台塔截角立方體	15.542472333	$8+{\frac {16{\sqrt {2}}}{3}}$
67	對二側帳塔截角立方體	17.485281374	$9+6{\sqrt {2}}$
68	側台塔截角十二面體	87.363709878	${\frac {505}{12}}+{\frac {81{\sqrt {5}}}{4}}$
69	對二側台塔截角十二面體	89.687755196	${\frac {1}{12}}\left(515+251{\sqrt {5}}\right)$
70	間二側台塔截角十二面體	89.687755196	${\frac {1}{12}}\left(515+251{\sqrt {5}}\right)$
71	三側台塔截角十二面體	92.011800514	${\frac {7}{12}}\left(75+37{\sqrt {5}}\right)$
72	單旋側帳塔小斜方截半二十面體	41.615323782	$20+{\frac {29{\sqrt {5}}}{3}}$
73	對二旋側台塔小斜方截半二十面體	41.615323782	$20+{\frac {29{\sqrt {5}}}{3}}$
74	鄰二旋側台塔小斜方截半二十面體	41.615323782	$20+{\frac {29{\sqrt {5}}}{3}}$
75	三旋側台塔小斜方截半二十面體	41.615323782	$20+{\frac {29{\sqrt {5}}}{3}}$
76	小斜方截半二十面體欠一側台塔	39.291278464	${\frac {115}{6}}+9{\sqrt {5}}$
77	對單旋側台塔小斜方截半二十面體欠一側台塔	39.291278464	${\frac {115}{6}}+9{\sqrt {5}}$
78	鄰單旋側台塔小斜方截半二十面體欠一側台塔	39.291278464	${\frac {115}{6}}+9{\sqrt {5}}$
79	二旋側台塔小斜方截半二十面體欠一側台塔	39.291278464	${\frac {115}{6}}+9{\sqrt {5}}$
80	小斜方截半二十面體欠對二側帳塔	36.967233146	${\frac {5}{3}}\left(11+5{\sqrt {5}}\right)$
81	小斜方截半二十面體欠鄰二側帳塔	36.967233146	${\frac {5}{3}}\left(11+5{\sqrt {5}}\right)$
82	單旋側台塔小斜方截半二十面體欠二側台塔	36.967233146	${\frac {5}{3}}\left(11+5{\sqrt {5}}\right)$
83	小斜方截半二十面體欠三側台塔	34.643187827	${\frac {35}{2}}+{\frac {23{\sqrt {5}}}{3}}$
84	扭稜鍥形體	0.859493646	6次方程的根
85	扭稜四角反角柱	3.601222010	12次方程的根
86	球狀屋頂	1.515351640	${\frac {1}{2}}{\sqrt {1+3{\sqrt {\frac {3}{2}}}+{\sqrt {13+3{\sqrt {6}}}}}}$
87	側錐球狀屋頂	1.751053900	16次方程的根
88	加長型球狀屋頂	1.948108229	32次方程的根
89	廣底加長型球狀屋頂	2.912910415	20次方程的根
90	五角錐球狀屋頂	3.777645342	24次方程的根
91	雙新月雙罩帳	3.093717650	${\frac {1}{12}}\left(17+9{\sqrt {5}}\right)$
92	三角廣底球狀罩帳	5.108745974	${\frac {5}{2}}+{\frac {7{\sqrt {5}}}{6}}$

在固定邊長的條件下，正四角錐 $J 1$ 和雙三角錐 $J 12$ 的體積最小；而三側台塔截角十二面體 $J 71$ 的體積最大，比前者大超過390倍。

在92種詹森多面體中，有13種詹森多面體的體積 $V / a 3$ 無法表達為解析數。這些數值是以下多項式的最大實根。

$J n$	多項式
23	$6561 x 8 - 52488 x 7 + 113724 x 6 - 9720 x 5 - 1616922 x 4 + 396360 x 3 + 1537020 x 2 - 178632 x - 3391$
24	$1679616 x 8 - 11197440 x 7 + 27060480 x 6 + 35769600 x 5 - 4456749600 x 4 - 10714248000 x 3 + 3828402000 x 2 + 13859430000 x + 5340175625$
25	$1679616 x 8 - 50388480 x 7 + 603262080 x 6 - 3520972800 x 5 + 5215460400 x 4 + 4128624000 x 3 - 8894943000 x 2 + 3881385000 x - 424924375$
45	$6561 x 8 - 104976 x 7 + 594864 x 6 - 1384128 x 5 - 552096 x 4 + 1569024 x 3 + 246528 x 2 - 119808 x + 4352$
46	$6561 x 8 - 87480 x 7 + 313470 x 6 + 753300 x 5 - 22424850 x 4 - 84591000 x 3 - 85909500 x 2 + 8715000 x + 35547500$
47	$1679616 x 8 - 61585920 x 7 + 851472000 x 6 - 5108832000 x 5 + 4745790000 x 4 + 21346200000 x 3 - 29019375000 x 2 - 4576875000 x - 405859375$
48	$6561 x 8 - 393660 x 7 + 9316620 x 6 - 108207900 x 5 + 601832025 x 4 - 1417189500 x 3 + 965841750 x 2 + 597667500 x - 668786875$
84	$5832 x 6 - 1377 x 4 - 2160 x 2 - 4$
85	$531441 x 12 - 85726026 x 8 - 48347280 x 6 + 11588832 x 4 + 4759488 x 2 - 892448$
87	$45137758519296 x 16 - 110336743047168 x 14 - 191069246324736 x 12 + 209269081571328 x 10 + 364547659290624 x 8 - 58793017190400 x 6 + 3306865979520 x 4 - 1275399855936 x 2 + 1439671249$
88	$521578814501447328359509917696 x 32 - 985204427391622731345740955648 x 30 - 16645447351681991898880656015360 x 28 + 79710816694053483249372512649216 x 26 - 152195045391070538203422101864448 x 24 + 156280253448056209478031589244928 x 22 - 96188116617075838858708654227456 x 20 + 30636368373570166303441645731840 x 18 + 5828527077458909552923002273792 x 16 - 8060049780765551057159394951168 x 14 + 1018074792115156107372011716608 x 12 + 35220131544370794950945931264 x 10 + 327511698517355918956755959808 x 8 - 116978732884218191486738706432 x 6 + 10231563774949176791703149568 x 4 - 366323949299263261553952192 x 2 + 3071435678740442112675625$
89	$47330370277129322496 x 20 - 722445512980071186432 x 18 + 3596480447590271287296 x 16 - 8432333285523990773760 x 14 + 8973584611317745975296 x 12 - 3065290664181478981632 x 10 + 366229890219212144640 x 8 - 8337259437908852736 x 6 - 22211277300912896 x 4 + 132615435213216 x 2 + 2693461945329$
90	$1213025622610333925376 x 24 + 54451372392730545094656 x 22 - 796837093078664749252608 x 20 - 4133410366404688544268288 x 18 + 20902529024429842816303104 x 16 - 133907540390420673677230080 x 14 + 246234688242991598853881856 x 12 - 63327534106871321714442240 x 10 + 14389309497459555704164608 x 8 + 48042947402464500749392128 x 6 - 5891096640600351061013664 x 4 - 3212114716816853362953264 x 2 + 479556973248657693884401$

內切球半徑、中分球半徑和外接球半徑

下表列出了存在內切球、中分球和外接球之詹森多面體的各種球半徑（內切球半徑 $R i$ 、中分球半徑 $R m$ 或外接球半徑 $R c$ ，不存在則不列出）與邊長之比。

詹森多面體不一定有內切球、中分球和外接球。比方說，除非該詹森多面體的所有頂點都位於某個球面上，否則這個詹森多面體不會存在外接球。詹森多面體的對稱性比正多面體低，因此很多詹森多面體不存在這些球體。只有正四角錐 $J 1$ 和正五角錐 $J 2$ 這兩個立體三種球都存在。

表格內容的資料來源是來自沃尔夫勒姆研究公司的Mathematica軟體提供的PolyhedronData[..., "Inradius"]、 PolyhedronData[..., "Midradius"]和 PolyhedronData[..., "Circumradius"]指令。輸出的數值已被化簡過了。

$J n$	$R i /a$ （近似值）	$R i /a$ （精確值）	$R m /a$ （近似值）	$R m /a$ （精確值）	$R c /a$ （近似值）	$R c /a$ （精確值）
1	0.258819045	${\frac {\sqrt {2-{\sqrt {3}}}}{2}}$	0.500000000	${\frac {1}{2}}$	0.707106781	${\frac {1}{\sqrt {2}}}$
2	0.232788309	${\frac {1}{\sqrt {25-7{\sqrt {5}}+{\sqrt {30\left(5-{\sqrt {5}}\right)}}}}}$	0.809016994	${\frac {1}{4}}\left(1+{\sqrt {5}}\right)$	0.951056516	${\frac {1}{2}}{\sqrt {{\frac {1}{2}}\left(5+{\sqrt {5}}\right)}}$
3	-	-	0.866025404	${\frac {\sqrt {3}}{2}}$	1.000000000	$1$
4	-	-	1.306562965	${\sqrt {1+{\frac {1}{\sqrt {2}}}}}$	1.398966326	${\sqrt {{\frac {5}{4}}+{\frac {1}{\sqrt {2}}}}}$
5	-	-	2.176250899	${\sqrt {{\frac {5}{2}}+{\sqrt {5}}}}$	2.232950509	${\frac {1}{2}}{\sqrt {11+4{\sqrt {5}}}}$
6	-	-	1.538841769	${\frac {1}{2}}{\sqrt {5+2{\sqrt {5}}}}$	1.618033989	${\frac {1}{2}}\left(1+{\sqrt {5}}\right)$
7	-	-	-	-	-	-
8	-	-	-	-	-	-
9	-	-	-	-	-	-
10	-	-	-	-	-	-
11	-	-	0.809016994	${\frac {1}{4}}\left(1+{\sqrt {5}}\right)$	0.951056516	${\frac {1}{2}}{\sqrt {{\frac {1}{2}}\left(5+{\sqrt {5}}\right)}}$
12	0.272165527	${\frac {\sqrt {\frac {2}{3}}}{3}}$	-	-	-	-
13	0.417774579	${\sqrt {{\frac {1}{30}}\left(3+{\sqrt {5}}\right)}}$	-	-	-	-
14	-	-	-	-	-	-
15	-	-	-	-	-	-
16	-	-	-	-	-	-
17	-	-	-	-	-	-
18	-	-	-	-	-	-
19	-	-	1.306562965	${\sqrt {1+{\frac {1}{\sqrt {2}}}}}$	1.398966326	${\sqrt {{\frac {5}{4}}+{\frac {1}{\sqrt {2}}}}}$
20	-	-	-	-	-	-
21	-	-	-	-	-	-
22	-	-	-	-	-	-
23	-	-	-	-	-	-
24	-	-	-	-	-	-
25	-	-	-	-	-	-
26	-	-	-	-	-	-
27	-	-	0.866025404	${\frac {\sqrt {3}}{2}}$	1.000000000	$1$
28	-	-	-	-	-	-
29	-	-	-	-	-	-
30	-	-	-	-	-	-
31	-	-	-	-	-	-
32	-	-	-	-	-	-
33	-	-	-	-	-	-
34	-	-	1.538841769	${\frac {1}{2}}{\sqrt {5+2{\sqrt {5}}}}$	1.618033989	${\frac {1}{2}}\left(1+{\sqrt {5}}\right)$
35	-	-	-	-	-	-
36	-	-	-	-	-	-
37	-	-	1.306562965	${\sqrt {1+{\frac {1}{\sqrt {2}}}}}$	1.398966326	${\sqrt {{\frac {5}{4}}+{\frac {1}{\sqrt {2}}}}}$
38	-	-	-	-	-	-
39	-	-	-	-	-	-
40	-	-	-	-	-	-
41	-	-	-	-	-	-
42	-	-	-	-	-	-
43	-	-	-	-	-	-
44	-	-	-	-	-	-
45	-	-	-	-	-	-
46	-	-	-	-	-	-
47	-	-	-	-	-	-
48	-	-	-	-	-	-
49	-	-	-	-	-	-
50	-	-	-	-	-	-
51	-	-	-	-	-	-
52	-	-	-	-	-	-
53	-	-	-	-	-	-
54	-	-	-	-	-	-
55	-	-	-	-	-	-
56	-	-	-	-	-	-
57	-	-	-	-	-	-
58	-	-	-	-	-	-
59	-	-	-	-	-	-
60	-	-	-	-	-	-
61	-	-	-	-	-	-
62	-	-	0.809016994	${\frac {1}{4}}\left(1+{\sqrt {5}}\right)$	0.951056516	${\frac {1}{2}}{\sqrt {{\frac {1}{2}}\left(5+{\sqrt {5}}\right)}}$
63	-	-	0.809016994	${\frac {1}{4}}\left(1+{\sqrt {5}}\right)$	0.951056516	${\frac {1}{2}}{\sqrt {{\frac {1}{2}}\left(5+{\sqrt {5}}\right)}}$
64	-	-	-	-	-	-
65	-	-	-	-	-	-
66	-	-	-	-	-	-
67	-	-	-	-	-	-
68	-	-	-	-	-	-
69	-	-	-	-	-	-
70	-	-	-	-	-	-
71	-	-	-	-	-	-
72	-	-	2.176250899	${\sqrt {{\frac {5}{2}}+{\sqrt {5}}}}$	2.232950509	${\frac {1}{2}}{\sqrt {11+4{\sqrt {5}}}}$
73	-	-	2.176250899	${\sqrt {{\frac {5}{2}}+{\sqrt {5}}}}$	2.232950509	${\frac {1}{2}}{\sqrt {11+4{\sqrt {5}}}}$
74	-	-	2.176250899	${\sqrt {{\frac {5}{2}}+{\sqrt {5}}}}$	2.232950509	${\frac {1}{2}}{\sqrt {11+4{\sqrt {5}}}}$
75	-	-	2.176250899	${\sqrt {{\frac {5}{2}}+{\sqrt {5}}}}$	2.232950509	${\frac {1}{2}}{\sqrt {11+4{\sqrt {5}}}}$
76	-	-	2.176250899	${\sqrt {{\frac {5}{2}}+{\sqrt {5}}}}$	2.232950509	${\frac {1}{2}}{\sqrt {11+4{\sqrt {5}}}}$
77	-	-	2.176250899	${\sqrt {{\frac {5}{2}}+{\sqrt {5}}}}$	2.232950509	${\frac {1}{2}}{\sqrt {11+4{\sqrt {5}}}}$
78	-	-	2.176250899	${\sqrt {{\frac {5}{2}}+{\sqrt {5}}}}$	2.232950509	${\frac {1}{2}}{\sqrt {11+4{\sqrt {5}}}}$
79	-	-	2.176250899	${\sqrt {{\frac {5}{2}}+{\sqrt {5}}}}$	2.232950509	${\frac {1}{2}}{\sqrt {11+4{\sqrt {5}}}}$
80	-	-	2.176250899	${\sqrt {{\frac {5}{2}}+{\sqrt {5}}}}$	2.232950509	${\frac {1}{2}}{\sqrt {11+4{\sqrt {5}}}}$
81	-	-	2.176250899	${\sqrt {{\frac {5}{2}}+{\sqrt {5}}}}$	2.232950509	${\frac {1}{2}}{\sqrt {11+4{\sqrt {5}}}}$
82	-	-	2.176250899	${\sqrt {{\frac {5}{2}}+{\sqrt {5}}}}$	2.232950509	${\frac {1}{2}}{\sqrt {11+4{\sqrt {5}}}}$
83	-	-	2.176250899	${\sqrt {{\frac {5}{2}}+{\sqrt {5}}}}$	2.232950509	${\frac {1}{2}}{\sqrt {11+4{\sqrt {5}}}}$
84	-	-	-	-	-	-
85	-	-	-	-	-	-
86	-	-	-	-	-	-
87	-	-	-	-	-	-
88	-	-	-	-	-	-
89	-	-	-	-	-	-
90	-	-	-	-	-	-
91	-	-	-	-	-	-
92	-	-	-	-	-	-

參見

詹森多面體

參考文獻

Johnson, Norman W. . Canadian Journal of Mathematics. 1966, 18: 169–200. ISSN 0008-414X. Zbl 0132.14603. doi:10.4153/cjm-1966-021-8 .
Zalgaller, Victor A. . Zap. Nauchn. Semin. Leningr. Otd. Mat. Inst. Steklova. 1967, 2: 1–221. ISSN 0373-2703. Zbl 0165.56302 （俄语）.
Robert R Tupelo-Schneck. . [2023-01-31]. （原始内容存档于2021-08-18）.
Timofeenko, Aleksei Victorovich. . Algebra i Analiz (St. Petersburg Department of Steklov Institute of Mathematics, Russian~…). 2009, 21 (3): 165–209.
D. Eppstein. . www.ics.uci.edu. [2022-05-25]. （原始内容存档于2021-01-26）.

外部連結

Sylvain Gagnon, "Convex polyhedra with regular faces", Structural Topology, No. 6, 1982, 83-95.
Johnson Solids （页面存档备份，存于） by George W. Hart.
Images of all 92 solids, categorized, on one page
埃里克·韦斯坦因. . MathWorld.
VRML models of Johnson Solids （页面存档备份，存于） by Jim McNeill
VRML models of Johnson Solids （页面存档备份，存于） by Vladimir Bulatov

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] Johnson, Norman W. . Canadian Journal of Mathematics. 1966, 18: 169–200. ISSN 0008-414X. Zbl 0132.14603. doi:10.4153/cjm-1966-021-8 .

[2] Zalgaller, Victor A. . Zap. Nauchn. Semin. Leningr. Otd. Mat. Inst. Steklova. 1967, 2: 1–221. ISSN 0373-2703. Zbl 0165.56302 （俄语）.

[Robert_R_Tupelo-Schneck_conditional_edges-3] Robert R Tupelo-Schneck. . [2023-01-31]. （原始内容存档于2021-08-18）.

[article_timofeenko2009junction-4] Timofeenko, Aleksei Victorovich. . Algebra i Analiz (St. Petersburg Department of Steklov Institute of Mathematics, Russian~…). 2009, 21 (3): 165–209.

[5] D. Eppstein. . www.ics.uci.edu. [2022-05-25]. （原始内容存档于2021-01-26）.