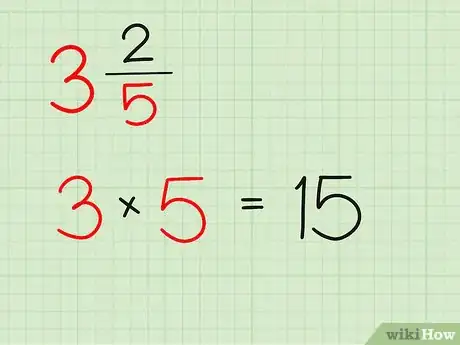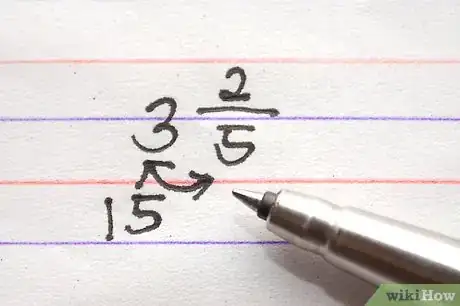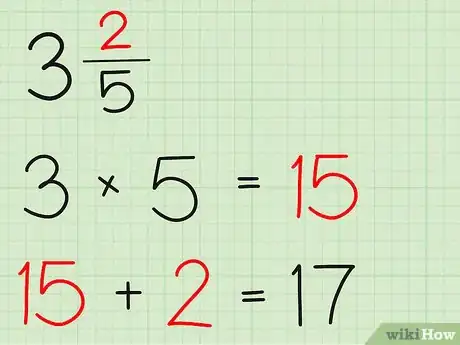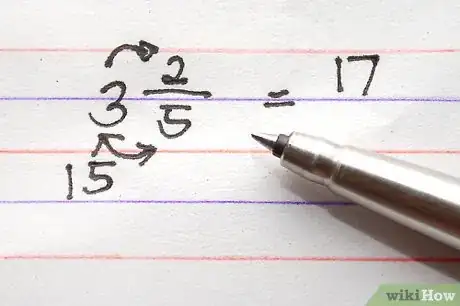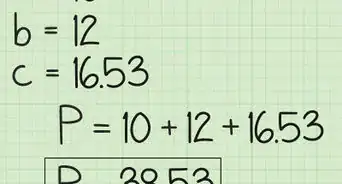X
wikiHow是一个“多人协作写作系统”,因此我们的很多文章都是由多位作者共同创作的。 为了创作这篇文章,62位用户(部分匿名)多次对文章进行了编辑和改进。
这篇文章已经被读过22,689次。
分数问题乍一眼看起来棘手,但是随着你的练习和诀窍的掌握,它们就会变得比较容易。下面就教你如何解答分数问题。
步骤
方法 1
方法 1 的 4:
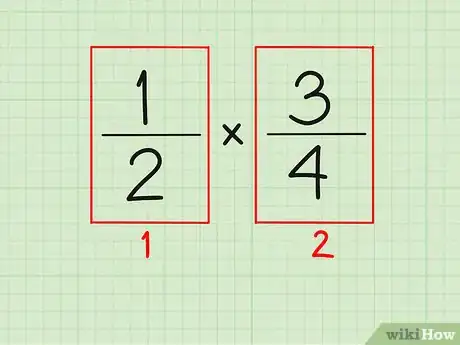
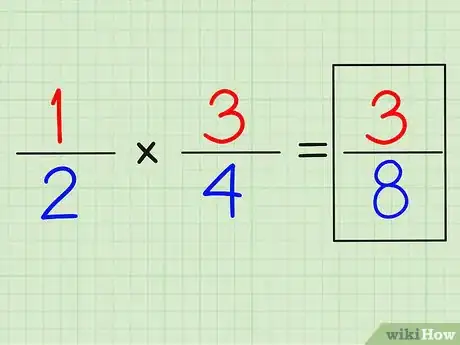
分数乘法
方法 2
方法 2 的 4:
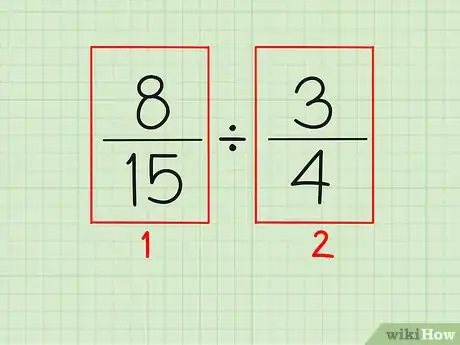
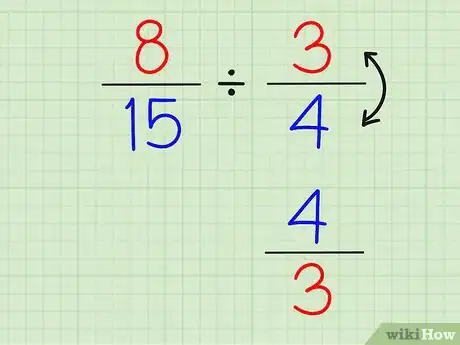
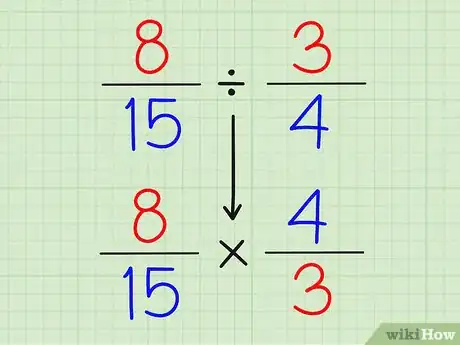
分数除法
方法 3
方法 3 的 4:
带分数转换成假分数
方法 4
方法 4 的 4:
分数加减
-
找到最小公分母(底部数字),不管是分数的加法还是减法,你都得经过这个过程。约分成最简分数,以便之后转换最小公分母进行运算。
- 举个例子,如果你遇到的数字是1/4和1/6,那么它们的最小公约数是12.(4x3=12, 6x2=12)
-
分数乘法时一定要找最小公分母。记住,当你这样做时并没有改变分数的数额,而只是改变了它的表达方式,分数的本质并没有变。想象一下比萨饼,1/2个比萨饼跟2/4个比萨饼是同样的数量。(4x3=12, 6x2=12)
- 找出当前的分母要扩大多少倍才能得到最小公分母。例如1/4,4乘3得12;1/6,6乘2得12(所以1/4和1/6的最小公分母是12)。
- 同时把分母和分子与那个数相乘。例如1/4,把1和4分别同3相乘,得到3/12.1/6上下同时乘2,得到2/12.现在你要解决的问题就是3/12 + 2/12或3/12 - 2/12。
-
把这两个数的分子相加减(注意不是分母)。这其中的奥妙在于你是想得到总共有多少个这种类型的分数。如果你同时也把分母加减了,你就会改变分数的类型。
- 例如3/12 + 2/12,你最终的答案是5/12。而对于3/12 - 2/12,结果就是1/12。
广告
小提示
- 掌握四项基本的运算方法(乘法、除法、加法、减法),将有助于你轻松、快速掌握这个环节。
- 在做乘除的时候,你可以不用第一时间将带分数转化成假分数。但是这样做可能会导致更复杂地使用分配率。所以通常还是最好首先将带分数转化成假分数。
- 要想得到整数的倒数,只要把1放在整数头上就可以了。例如,5的倒数就变成了1/5.
- “把分数颠倒“的另一个说法就是”求这个分数的倒数“。你只需要将分子和分母上下对换。例如,2/4的倒数得到4/2.
- 当你求一个负数的倒数时,负号停留在分子。
广告
警告
- 在运算之前将带分数转化成假分数
- 和你的老师核对是否需要将运算结果约到最简分数。
- 例如,2/5是最简分数,而16/40不是。
- 和你的老师核对是否需要把假分数化成带分数。
- 例如,把13/4化为3 1/4。
广告
关于本wikiHow
广告