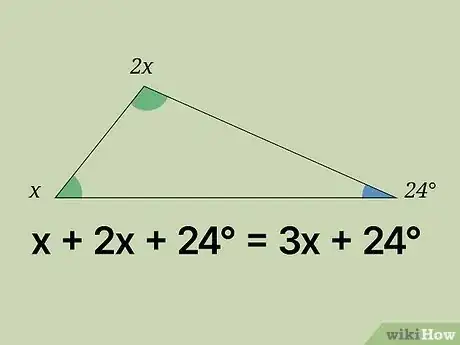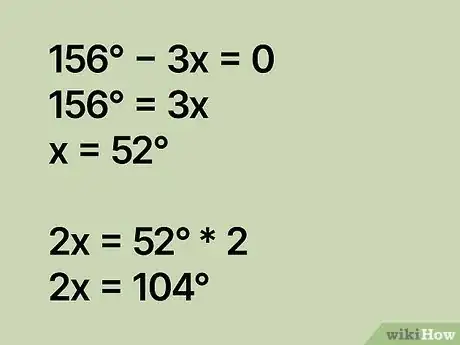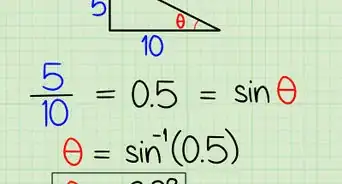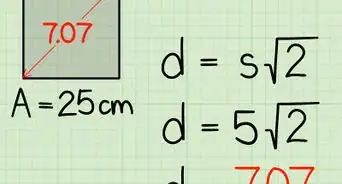如何求三角形的第三个角

共同创作者是 Grace Imson, MA

当你已知三角形其中两个角的角度后，求第三个角的大小并不是件难事。你只需要用180°减去已知的两个角度即可得到第三个角的大小。然而，我们也有计算第三个角的其他方法，具体使用哪种方法则取决于你正处理的问题是哪样的。如果你想要学习如何求复杂难题中的三角形第三个角度大小，那么阅读本文来学习求解方法吧。

方法 1

方法 1 的 3:

借助于另外两个角的大小

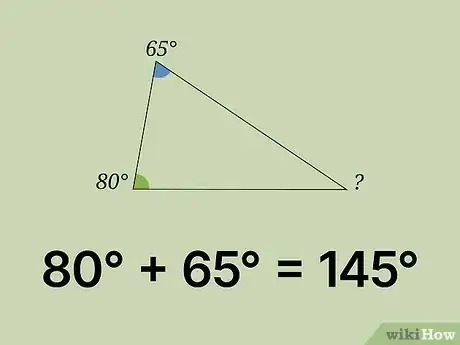
你需要借助三角形的内角和定理，即所有三角形的内角相加得到的和永远是180°。该定理是亘古不变的真理。因此，如果你已知三角形的两个角求第三个角的大小，那么你首先要将已知的两个角的角度相加。例如，你已知某三角形的两个角是80°和65°。那么将其相加，(80° + 65°)得到145°。
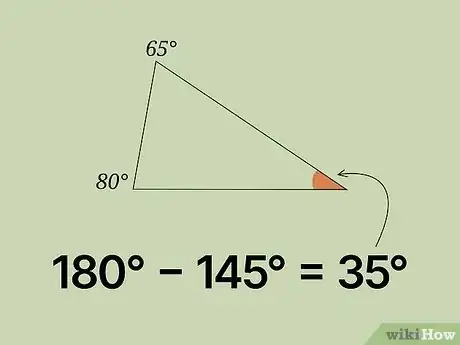
根据内角和定理，我们知道三角形内角之和为180°。那么，已知的两角加上未知的第三个角的结果一定是180°。在本例中，180° - 145° = 35°。
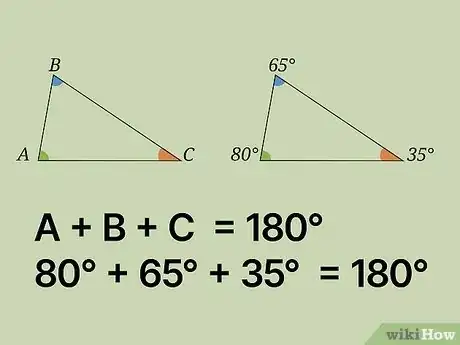
现在已计算出剩余第三个角的大小为35°。如果你不放心自己的计算，那么你可以再检查一下。你可以再次将三角形的三个内角相加，如果得到180°，那么你的计算结果无误。在本例中，80° + 65° + 35° = 180°。至此，问题已解决。

广告

方法 2

方法 2 的 3:

使用变量计算角度

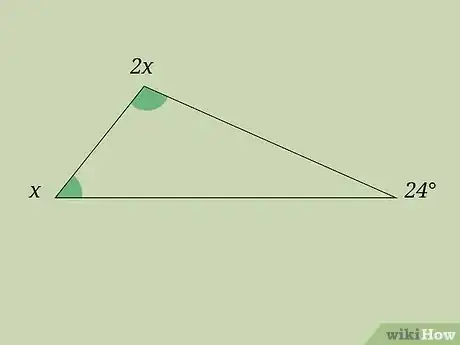
有时候，你可能没有那么幸运地已知两个角的大小，而是已知几个变量或者几个变量和一个角度。例如在本例中，我们已知三角形的三个内角分别是"x," "2x,"和24"，然后求x的大小。首先，先将已知的信息写下来。
此处我们遵循的定理与上部分的内角和一致。我们将三角形所有的角度（包括变量）相加，得到x + 2x + 24° = 3x + 24°.
3
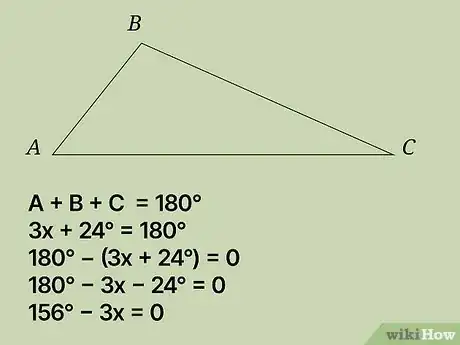
用180°减去三角和。将三角相加后，用180来减去上步结果得到0。步骤如下：
- 180° - (3x + 24°) = 0
- 180° - 3x - 24° = 0
- 156° - 3x = 0
现在化解等式将变量放在一侧，数值放在另一侧。你将得到156° = 3x。此时将等式两边同时除以3得到x = 52°。这就意味着，第三个角的大小是52°。另外一个未知角（2x）的大小是2 x 52°,即104°。
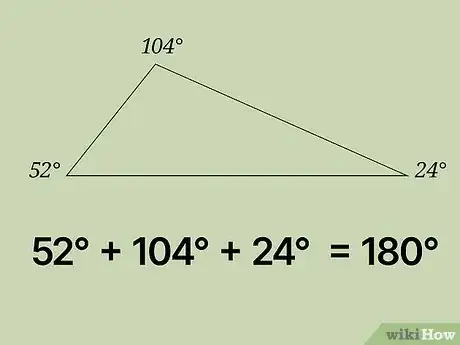
如果你想确保结果的正确性，那么将三个角的角度相加得到180°即可保证结果的正确。即52° + 104° + 24° = 180°。至此，问题已被正确解决。

广告

方法 3

方法 3 的 3:

使用其他方法求解

1
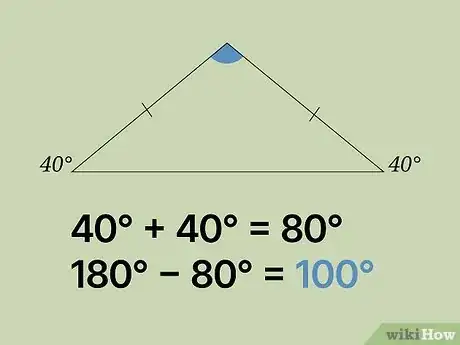
求等腰三角形的第三个角。等腰三角形的两个边（腰）相等，且有两个相等的角（底角）。其中其相等的边（腰）被斜条标记以显示两者相等。如果你已知其中一个底角的大小，那么你就能求出三个角的大小。具体方法如下：
- 如果一个底角的大小是40°，那么另一个底角的大小也是40°。并且，你可以用180°减去两个底角的和40° + 40° (即80°)来求第三个角的大小。具体步骤是180° - 80° = 100°，那么第三个角为100°。
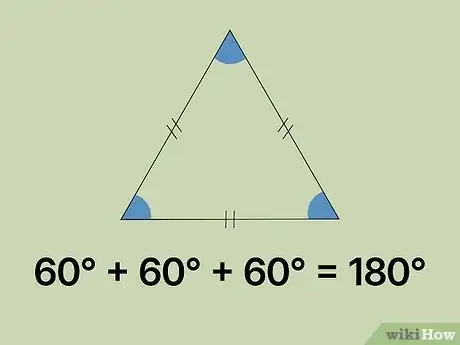
等边三角形的三边相等且三个内角大小相等。其三边的中间部分被两条斜线标记以表示三边相等。这也意味着等边三角形的三角相等且都为60°。你可以将三角相加来复查你的计算。具体方法如下：60° + 60° + 60° = 180°。
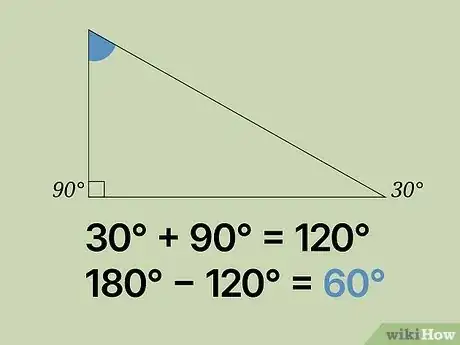
如果已知题目中的三角形为直角三角形，且已知一个角为30°。那么，你就已知两个角了，其中一个是直角90°，一个是30°的角。然后再利用三角形内角和定理，先将已知的两角相加(30° + 90° = 120°)，然后用180°减去该值。即180° - 120° = 60°。那么第三个角为60°。

广告

警告

如果加法计算或者减法计算中出现错误，那么会导致最终结果的错误。因此你最好多复查你的计算以防错误的产生。

广告

你可能还喜欢

广告

参考

关于本wikiHow

共同创作者是 :

Grace Imson, MA

数学教师

这篇文章的共同创作者是 Grace Imson, MA. Grace Imson是一位拥有逾40年教学经验的数学老师。她目前是美国旧金山城市学院的数学老师，之前曾在圣路易斯大学的数学系就职。Grace教过小学、初中、高中和大学水平的数学。她拥有圣路易斯大学的教育文学硕士学位，专攻教育管理与监督。这篇文章已经被读过15,080次。

分类: 教育与交流

广告