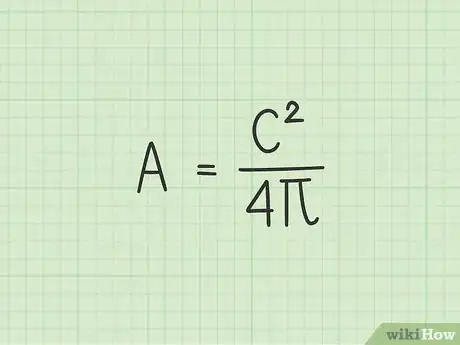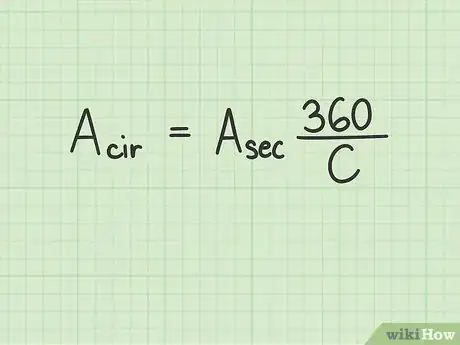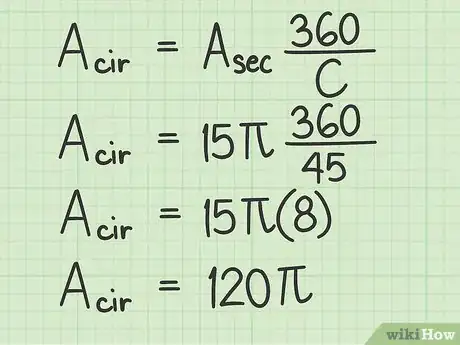如何计算圆面积

共同创作者是 Grace Imson, MA

需要计算圆面积？这是很常见的几何问题，要找出答案相当简单。大多数时候，你都能借助简单的数学公式 $A=\pi r^{2}$ 来计算。就算不知道半径，下面也会教你用直径、周长甚至是扇形面积算出圆面积。

方法 1

方法 1 的 4:

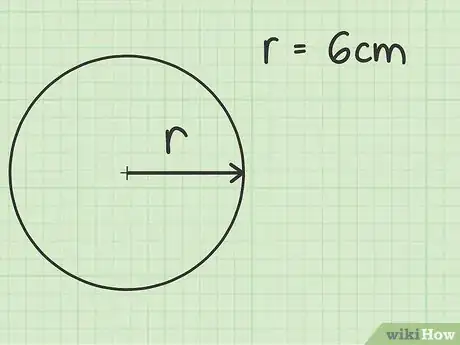
用半径计算圆面积

1
确认圆形的半径。半径是从圆心到圆周上任何一点所连成的线段。从任何方向测量半径都是一样的。半径也是直径的一半。直径是穿过圆心连接圆周上两点的线段。^{[1]
X
研究来源}
- 题目通常会标注圆心并给出半径。我们自己很难测量精确的圆心。
- 在这个例子中，假设圆形的半径为6厘米。
2
计算半径的平方。计算圆面积的公式是 $A=\pi r^{2}$ $A=\pi r^{2}$ ，其中 $r$ $r$ 变量指的就是半径。计算这个变量的平方。^{[2]
X
研究来源}
- 只是计算半径的平方，不是整个等式的平方。
- 在这个例子中， $r=6$ ，所以 $r^{2}=36$ 。
3
乘以圆周率。圆周率是圆形的周长与直径的比值，常用符号 $\pi$ $\pi$ 来表示。^{[3]
X
研究来源} $\pi$ $\pi$ 的近似值约等于3.14，但它其实是一个无限不循环小数。要精准描述圆面积，通常会用 $\pi$ $\pi$ 符号来书写答案。^{[4]
X
研究来源}
- 在这个例子中，半径是6厘米，圆面积的计算方法是：
  - $A=\pi r^{2}$
  - $A=\pi 6^{2}$
  - $A=36\pi$ 或 $A=36(3.14)=113.04$
4
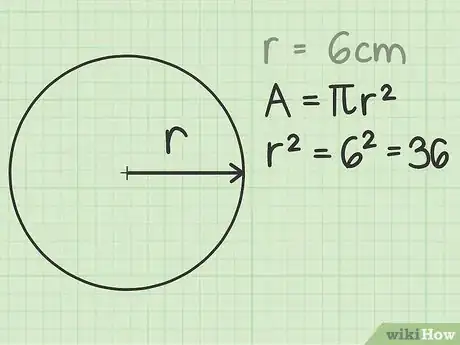
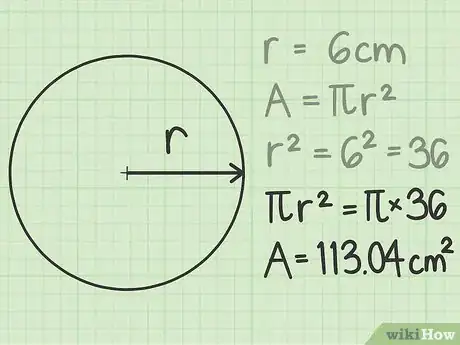
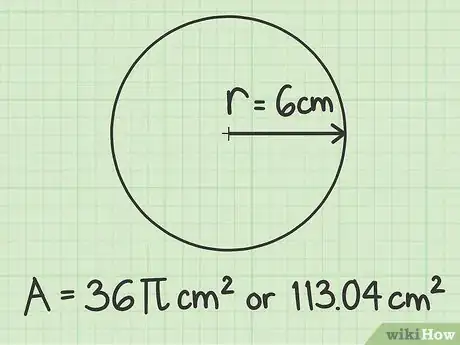
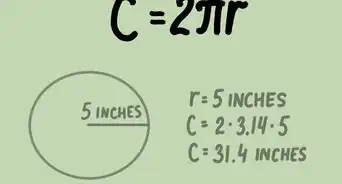
给出答案。记住，圆面积以平方为单位。如果半径的测量单位是厘米，那么圆面积的单位就是平方厘米。如果半径的测量单位是英尺，那么圆面积的单位就是平方英尺。你也应该弄清楚应该用符号 $\pi$ $\pi$ 还是近似值来书写答案。如果不知道，那就两个都写。^{[5]
X
研究来源}
- 在这个半径为6厘米的例子中，得出的圆面积是36 $\pi$ cm²或113.04 cm²。
广告

方法 2

方法 2 的 4:

用直径计算圆面积

1
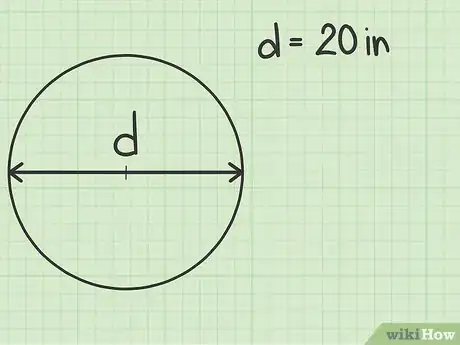
测量或记录直径。有些问题没有提供半径，而是给出直径。如果图上画了直径，你可以用尺来量。有的问题会直接给出直径的数值。
- 在这个例子中，假设圆形的直径为20英寸（50.8厘米）。
2
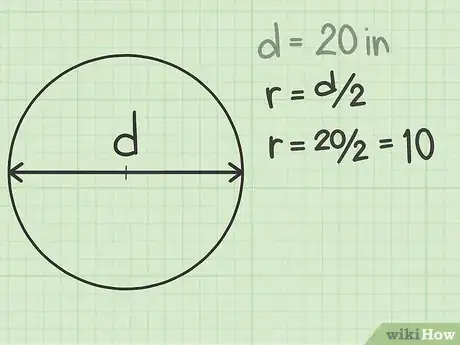
将直径除以2。记住，半径是直径的一半，所以不管直径的数值是多少，除以2就能得出半径。
- 所以，在这个例子中，圆形直径是20英寸（50.8厘米），半径就是20/2或10英寸（50.8/2或25.4厘米）。
3
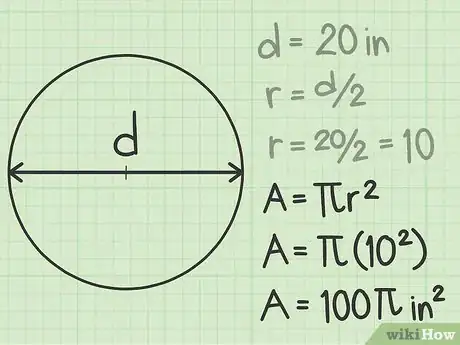
用原始的公式计算圆面积。用直径算出半径后，就能用 $A=\pi r^{2}$ $A=\pi r^{2}$ 公式来计算圆面积。放入半径的数值，然后按照下面的步骤完成剩下的计算：
- $A=\pi r^{2}$
- $A=\pi 10^{2}$
- $A=100\pi$
4
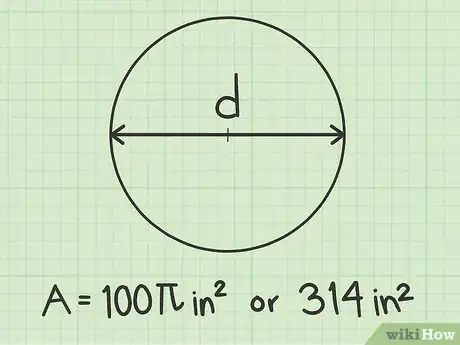
给出答案。记住，圆面积以平方为单位。在这个例子中，直径的测量单位是英寸，所以半径的单位也是英寸。计算出来的圆面积单位应该是平方英寸。在这个例子中，圆面积将会是 $100\pi$ $100\pi$ 平方英寸。
- 你也可以用3.14代替 $\pi$ ，算出圆面积的近似值。得出的答案将会是(100)(3.14) = 314平方英寸。
专家提示

Grace Imson, MA
旧金山城市学院数学老师
Grace Imson是一位拥有逾40年教学经验的数学老师。她目前是美国旧金山城市学院的数学老师，之前曾在圣路易斯大学的数学系就职。Grace教过小学、初中、高中和大学水平的数学。她拥有圣路易斯大学的教育文学硕士学位，专攻教育管理与监督。

Grace Imson, MA
旧金山城市学院数学老师

用直径计算圆面积最常犯的错误是忘记计算分母的平方。即使不将直径除以2得出半径，也有办法算出圆面积。但是，需要改一改公式，计算直径的平方，否则会得出错误的答案。

广告

方法 3

方法 3 的 4:

用周长计算圆面积

1
学习修正公式。如果你知道圆形的周长，就可以利用经过修正的公式计算出圆面积。这个修正公式直接使用周长算出面积，不需要知道半径。新的公式如下：
- $A={\frac {C^{2}}{4\pi }}$
2
测量或记录圆形周长。在真实的情况，你可能无法直接测量直径或半径。如果直径没有被画出来或是圆心没有被确认，你很难推测出圆心的位置。如果是有形的圆形物体，比如比萨盘或平底锅，用卷尺测量周长会比测量直径更准确。^{[6]
X
研究来源}
- 在这个例子中，假设你被告知或测量出圆形的周长为42厘米。
3
利用圆周和半径的关系来修正公式。圆形的周长等于pi乘以直径，可以写作 $C=\pi d$ $C=\pi d$ 。回想一下，直径是半径的两倍或 $d=2r$ $d=2r$ 。你可以将这两个等式结合在一起，创造出以下的关系： $C=\pi 2r$ $C=\pi 2r$ ，C即是圆周。重新排列一下，将 $r$ $r$ 的变量分隔出来：^{[7]
X
研究来源}
- $C=\pi 2r$
- ${\frac {C}{2\pi }}=r$ ...... （两边除以2 $\pi$ ）
4
将圆面积代入公式。你可以利用圆周和半径之间的关系，创造一个修正版的圆面积公式。将最新得到的等式代入原始的圆面积公式中：^{[8]
X
研究来源}
- $A=\pi r^{2}$ ......（原始的圆面积公式）
- $A=\pi ({\frac {C}{2\pi }})^{2}$ ......（代入直径的等式）
- $A=\pi ({\frac {C^{2}}{4\pi ^{2}}})$ ......（算出分数的平方）
- $A={\frac {C^{2}}{4\pi }}$ ......（将分子和分母里的 $\pi$ 抵消）
5
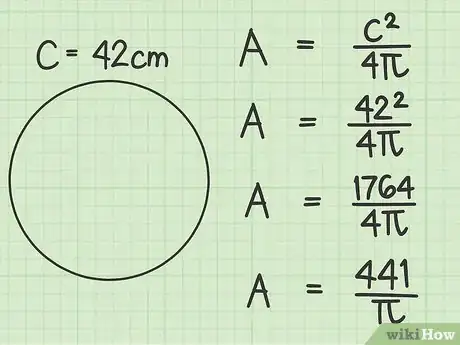
运用修正后的公式算出圆面积。这个修正公式使用周长代替半径，算出圆面积。放入周长的数值，然后按照下面的步骤进行计算：^{[9]
X
研究来源}
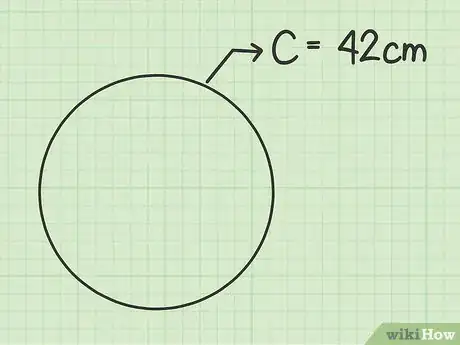
- 在这个例子中， $C=42$ 英寸（106.68厘米）。
- $A={\frac {C^{2}}{4\pi }}$
- $A={\frac {42^{2}}{4\pi }}$ ......（放入数值）
- $A={\frac {1764}{4\pi }}$ ......（计算42²）
- $A={\frac {441}{\pi }}$ ......（除以4）
6
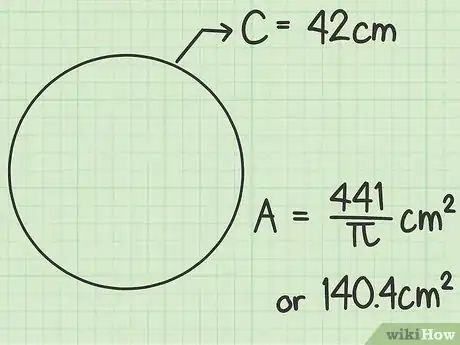
给出答案。除非题目给出的周长为 $\pi$ $\pi$ 的倍数，否则答案应该会是分数，而分母是 $\pi$ $\pi$ 。这个答案没有错，你也可以将它除以3.14，得出近似值。^{[10]
X
研究来源}
- 在这个例子中，圆周为42厘米，那么圆面积是 ${\frac {441}{\pi }}$ 平方厘米。
- 如果要计算近似值， ${\frac {441}{\pi }}={\frac {441}{3.14}}=140.4$ 。圆面积大概是140平方厘米。
广告

方法 4

方法 4 的 4:

从扇形面积计算出完整的圆面积

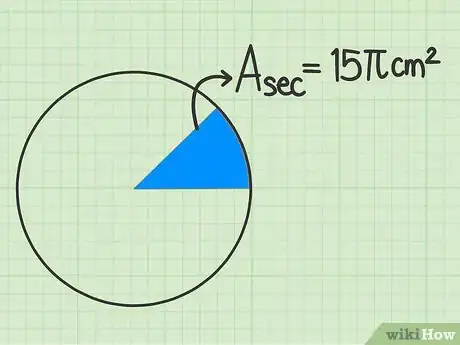
有些问题会告诉你扇形面积，然后要求你推导出完整的圆面积。仔细阅读题目，寻找类似这样的信息：“圆形O中的一个扇形面积为15 $\pi$ cm²。计算圆形O的面积。”^{[11]
X
研究来源}
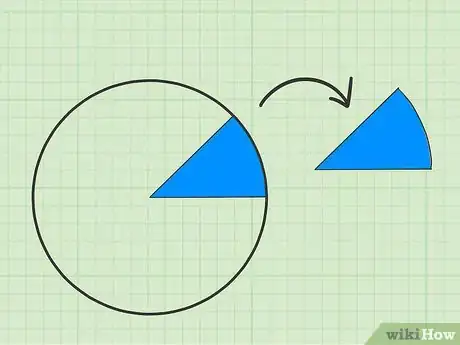
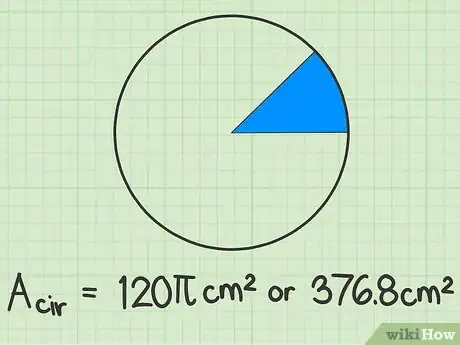
扇形是圆形上被两条半径和半径所截之一段弧所围成的图形，有时候也被称为“楔形”。从圆心处画两条半径到圆周。这两个半径之间的空间就是扇形。^{[12]
X
研究来源}
3
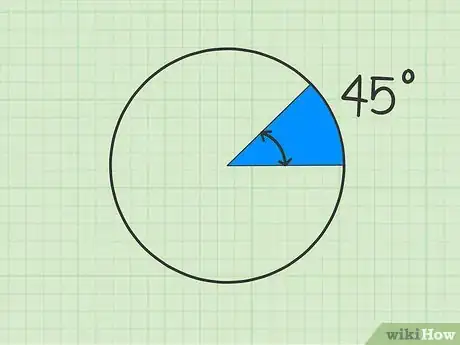
测量扇形的圆心角。用量角器测量两个半径之间的圆心角度。将量角器的底部边缘抵在一条半径上，量角器的中心点与圆心对齐。然后，读取跟构成扇形的第二条半径对应的角度读数。^{[13]
X
研究来源}
- 弄清楚究竟是测量两个半径之间的小角还是它们外侧的大角。题目应该会注明这一点。小角和大角的总和是360度。
- 有些题目会直接告诉你圆心角，不需要测量，比如：“扇形的圆心角是45度”。有的题目可能要求你自己测量圆心角。
4
用修正公式计算圆面积。只要知道扇形面积和圆心角，就能用以下的修正公式找出圆面积：^{[14]
X
研究来源}
- $A_{cir}=A_{sec}{\frac {360}{C}}$ $A_{cir}=A_{sec}{\frac {360}{C}}$
  - $A_{cir}$ 是完整的圆面积。
  - $A_{sec}$ 是扇形面积。
  - $C$ 是测量出的圆心角。
5
输入你知道的数值，计算出圆面积。在这个例子中，你被告知圆心角为45度，扇形面积为15 $\pi$ $\pi$ 。将这些数值放入公式中，然后按下面的步骤解答：^{[15]
X
研究来源}
- $A_{cir}=A_{sec}{\frac {360}{C}}$
- $A_{cir}=15\pi {\frac {360}{45}}$
- $A_{cir}=15\pi (8)$
- $A_{cir}=120\pi$
6
给出答案。在这个例子中，扇形面积是圆面积的八分之一。所以，完整的圆形面积是120 $\pi$ $\pi$ cm²。题目给出的扇形面积直接使用 $\pi$ $\pi$ ，所以你应该按同样的方式给出圆形面积。^{[16]
X
研究来源}
- 如果想要给出圆面积的近似值，将120乘以3.14，得出376.8 cm²的数值。
广告