如何计算均值、标准差和标准误差

收集数据后，你要做的第一件事往往就是对它进行分析。这通常都免不了要计算均值、标准差和标准误差。本文将向你展示如何计算。

方法 1

方法 1 的 4:

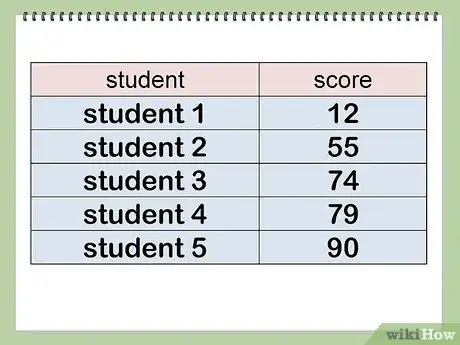
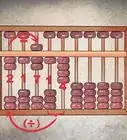
数据

1
获得一组你想要分析的数据。这些信息也称为样本。
- 例如，一个由5个学生组成的班级接受了一次测试，测试结果为12, 55, 74, 79和90。
广告

方法 2

方法 2 的 4:

均值

1
计算均值。把所有数值相加，再除以总体大小：
- 均值 (μ) = ΣX/N，这里的 Σ 是求和（加法）符号， x_i 是每个单一数值，而N则是总体大小。
- 在上例中，均值 μ 就是 (12+55+74+79+90)/5 = 62。

方法 3

方法 3 的 4:

标准差

1
计算标准差。它表征总体的分布情况。标准差 = σ = sqrt [(Σ((X-μ)^2))/(N)].
- 对以上给出的例子，标准差是 sqrt[((12-62)^2 + (55-62)^2 + (74-62)^2 + (79-62)^2 + (90-62)^2)/(5)] = 27.4。（注意，如果要求样本的标准差，则应除以n-1，即样本大小减1。
广告

方法 4

方法 4 的 4:

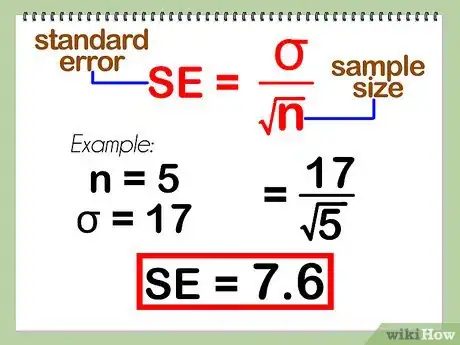
均值的标准误差

1
计算（均值的）标准误差。它表征的是样本均值与总体均值的近似度。样本越大，标准误差就越小，样本均值与总体均值也就越接近。将标准差除以样本大小N的平方根即可得出标准误差。标准误差 = σ/sqrt(n)
- 就以上的例子而言，如果从一个有50名学生的班级中抽取5个学生做样本，而50名学生的标准差为17 (σ = 21)，则标准误差即为 17/sqrt(5) = 7.6。

小提示

均值、标准差和标准误差的计算对于分析正态分布的数据最有用。距离中心位置1个标准差的范围覆盖了约68%的数据，距离其2个标准差的范围覆盖了95%的数据，而3个标准差能覆盖99.7%的数据。随着样本大小的增加，标准误差会变小（分布范围变窄）。
易用在线标准差计算器

广告

警告

仔细检查计算。计算中很容易出现失误，或是输入错误的数据。

广告

你可能还喜欢

广告

关于本wikiHow

wikiHow是一个“多人协作写作系统”，因此我们的很多文章都是由多位作者共同创作的。为了创作这篇文章，24位用户（部分匿名）多次对文章进行了编辑和改进。这篇文章已经被读过228,906次。

分类: 教育与交流

广告